Найти токи в схеме методом узлового напряжения если

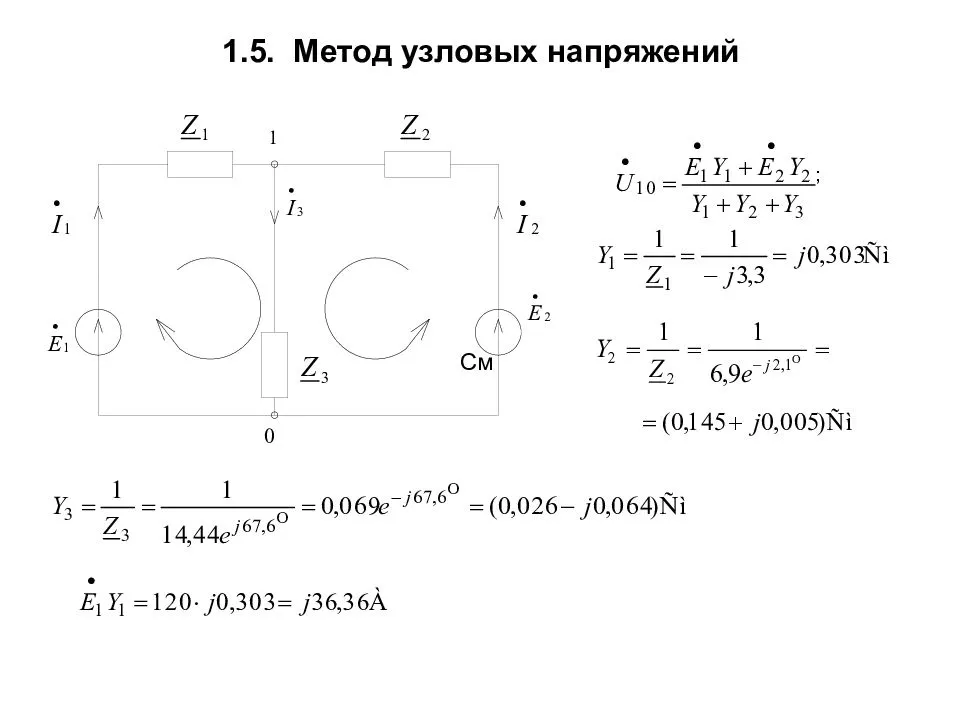
В полярной системе координат

Комплексное число можно представить в алгебраической, показательной и тригонометрической формах:

\displaystyle \dot{U_k}=U_k’+jU_k” = V_k \cdot e^{jδ_k} = V_k \big(\cos(δ_k)+j \sin(δ_k)\big).

Для того, чтобы вывести УУН в форме баланса мощностей в полярной системе координат, необходимо в систему подставить показательную запись комплексного числа \dot{U_k}. Выполнив это, получим:

\displaystyle \begin{cases}
V_i e^{-j δ_i} \sum_{k=1} \limits^{N} (g_{i \dot k} + j b_{i \dot k}) \cdot V_k \cdot e^{j δ_k} = P_i – j Q_i \end{cases}, i= \overline{ 1 \ldots (N-1) }.

Переносим экспоненты в одну сторону:

\displaystyle \begin{cases}
V_i\sum_{k=1}\limits^{N}V_k(g_{ik}+jb_{ik}) \cdot e^{jδ_k} \cdot e^{-jδ_i}=P_i-jQ_i\end{cases}, i= \overline{ 1 \ldots (N-1) }.

Используя свойство степеней, выполним преобразования:

\displaystyle \begin{cases}
V_i\sum_{k=1}\limits^{N} V_k (g_{ik}+jb_{ik}) \cdot e^{j(δ_k-δ_i)} = P_i – jQ_i\end{cases}, i= \overline{ 1 \ldots (N-1) }.

Переходим к тригонометрической форме:

\displaystyle \begin{cases}
V_i\sum_{k=1}\limits^{N} V_k \bigg( \big(g_{ik} + jb_{ik} \big) \big( \cos(δ_k-δ_i) + j \cdot \sin(δ_k-δ_i) \big) \bigg) = P_i-jQ_i
\end{cases}, i= \overline{ 1 \ldots (N-1) }.

Группируем относительно j:

(19)

\displaystyle \begin{cases}
V_i\sum_{k=1}\limits^{N}V_k \bigg( \big(g_{ik} \cdot \cos(δ_k-δ_i) – b_{ik} \cdot \sin(δ_k-δ_i) \big) + j \big(g_{ik} \cdot \sin(δ_k-δ_i) + b_{ik} \cdot \cos(δ_k-δ_i) \big) \bigg)
= P_i – jQ_i
\end{cases}, i= \overline{ 1 \ldots (N-1) }.

Преобразуем систему к виду, аналогичному системе , и получаем нелинейную систему УУН для сети переменного тока в полярных координатах в форме баланса мощностей:

(20)

\displaystyle \begin{cases}
V_i\sum_{k=1}\limits^{N}V_k \bigg(g_{ik} \cdot \cos(δ_k-δ_i) – b_{ik} \cdot \sin(δ_k-δ_i) \bigg)=P_i \\
V_i\sum_{k=1}\limits^{N}V_k \bigg(g_{ik} \cdot \sin(δ_k-δ_i) + b_{ik} \cdot \cos(δ_k-δ_i) \bigg)=-Q_i
\end{cases}, i= \overline{ 1 \ldots (N-1) } форма баланса мощностей.

Методы решения

Основные методы решения системы уравнений узловых напряжений:

1. Метод Гаусса-Зейделя — это один из самых первых разработанных методов. Обычно показывает более медленную сходимость по сравнению с другими итерационными методами. Основными особенности – это малое использование памяти и не требуется матричная алгебра.
2. Метод Якоби.
3. Метод Z-матриц.
4. Метод Ньютона-Рафсона — один из самых популярных методов решения, основанный на разложении в ряд Тейлора.
5. Метод голоморфного встраивания — прямой метод расчёта на основе комплексного анализа.

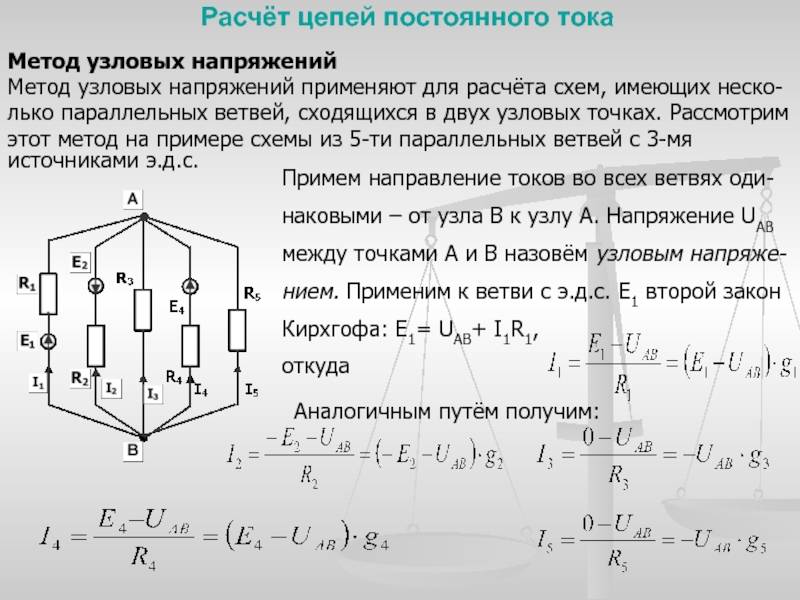
Электрическая цепь постоянного тока

Алгебраическая сумма падений напряжений на резистивных элементах в любом замкнутом контуре равно алгебраической сумме ЭДС. Нелинейный элемент, например лампа накаливания, имеет сопротивление, величина которого увеличивается при повышении напряжения, а следовательно и тока, подводимого к лампочке.
Источник электрической энергии характеризуется понятием ЭДС Е , под которой понимают величину, численно равную энергии, получаемой внутри источника единицей электрического заряда.
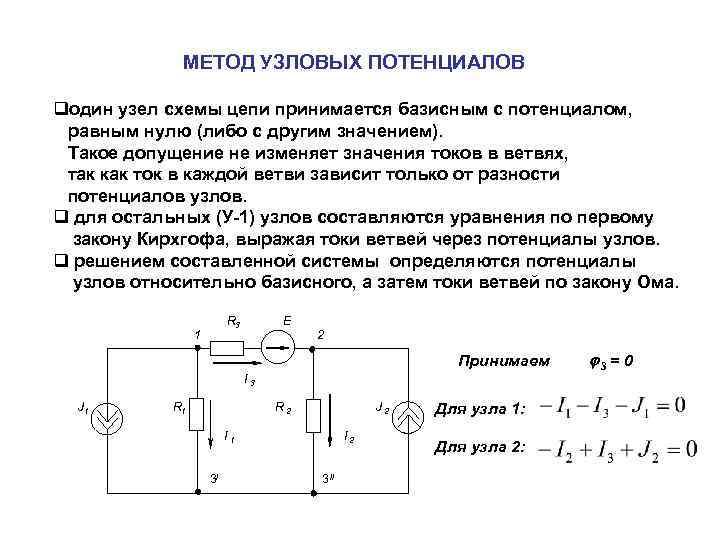
При расчете в схеме электрической цепи выделяют несколько основных элементов. Этот метод основан на составлении уравнений по первому закону Кирхгофа: Схема сложной электрической цепи с двумя узлами.
Для разных электротехнических устройств указывают свои номинальные параметры.
Электрическая цепь в режиме короткого замыкания имеет сопротивление, которое равно нулю. В этой схеме реальные элементы цепи изображаются условными обозначениями, причем вспомогательные элементы цепи обычно не изображаются, а если сопротивление соединительных проводов намного меньше сопротивления других элементов цепи, его не учитывают.
Как видно, при параллельном соединении источников ток и мощность внешней цепи равны соответственно сумме токов и мощностей источников.
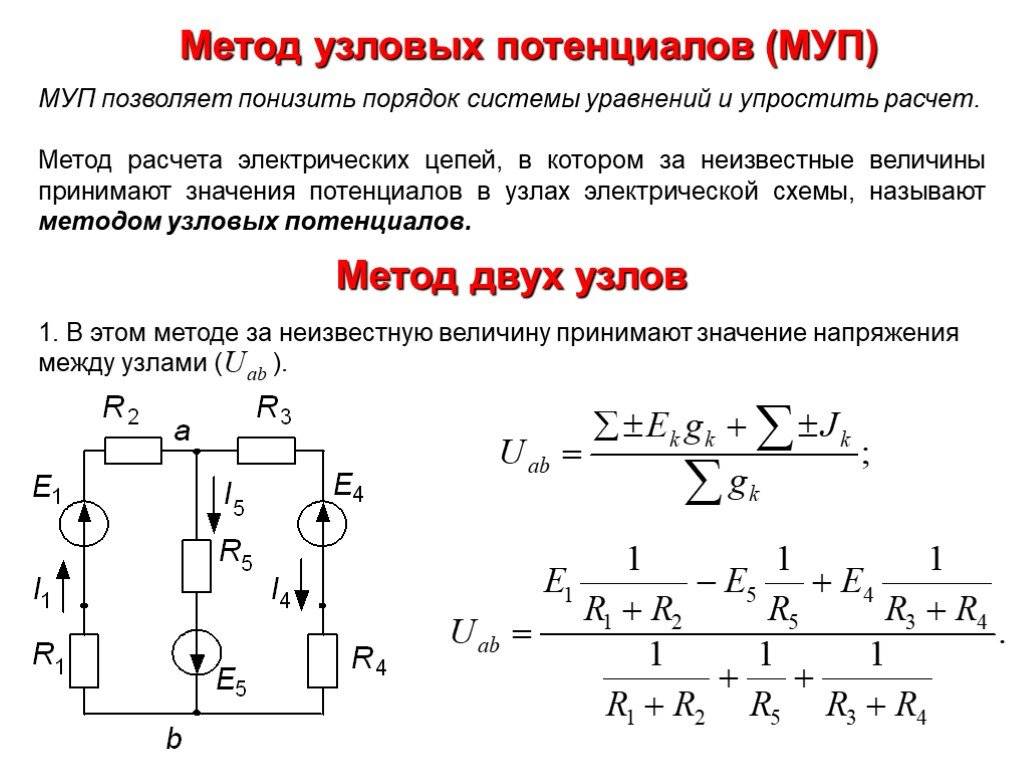
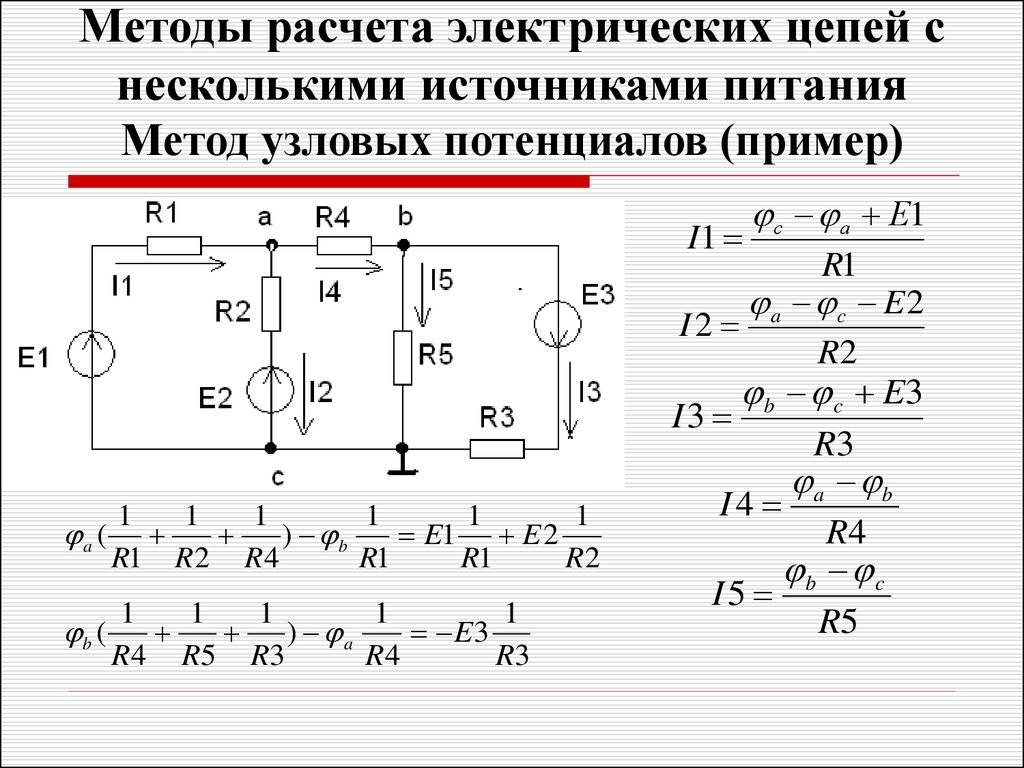
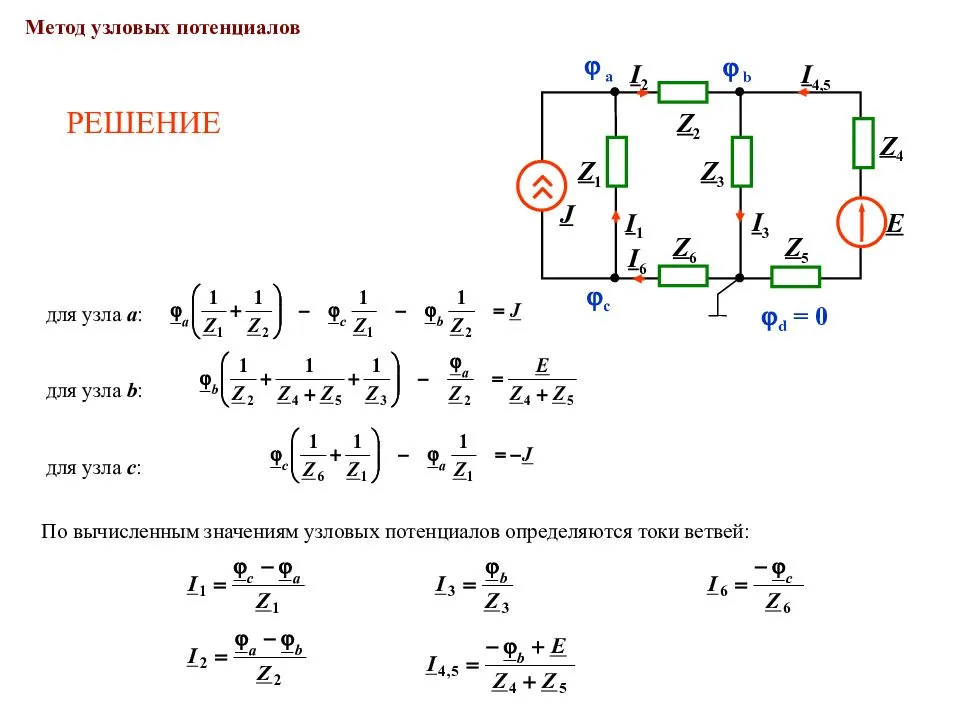
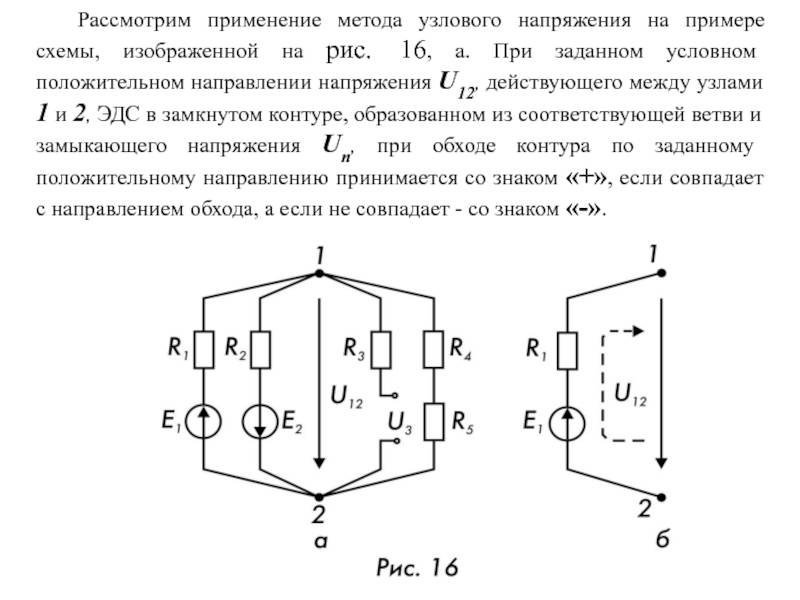
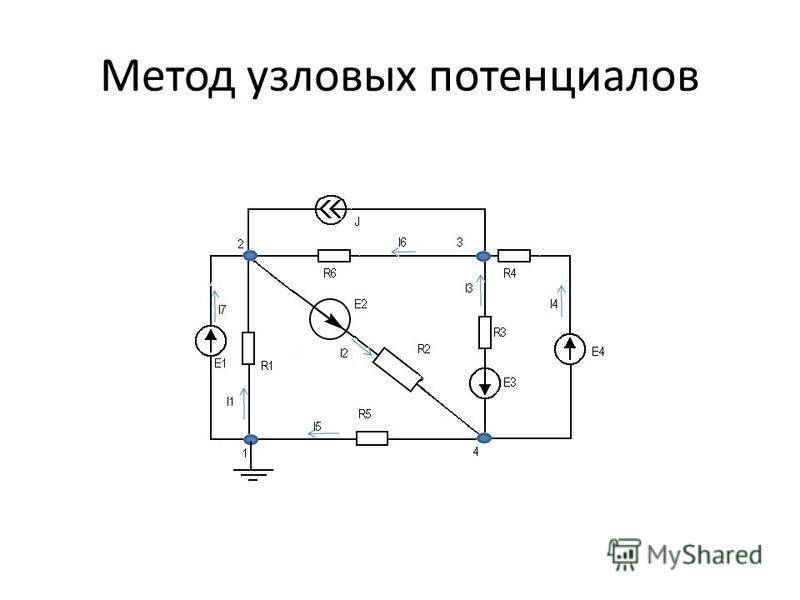
В случае последовательного соединения сопротивлений в ветви В общем виде уравнения узловых потенциалов имеют вид: Если в схеме имеются источники тока, то слагаемое в правой части будет равно сумме источников тока: Метод узловых потенциалов имеет преимущество, если число независимых узлов меньше числа контуров. Желательно во всех контурах положительные направления обхода выбирать одинаковыми, например, по часовой стрелке, как показано на рис.
Устройство и принцип работы двигателя постоянного тока. Схема двигателя постоянного тока.

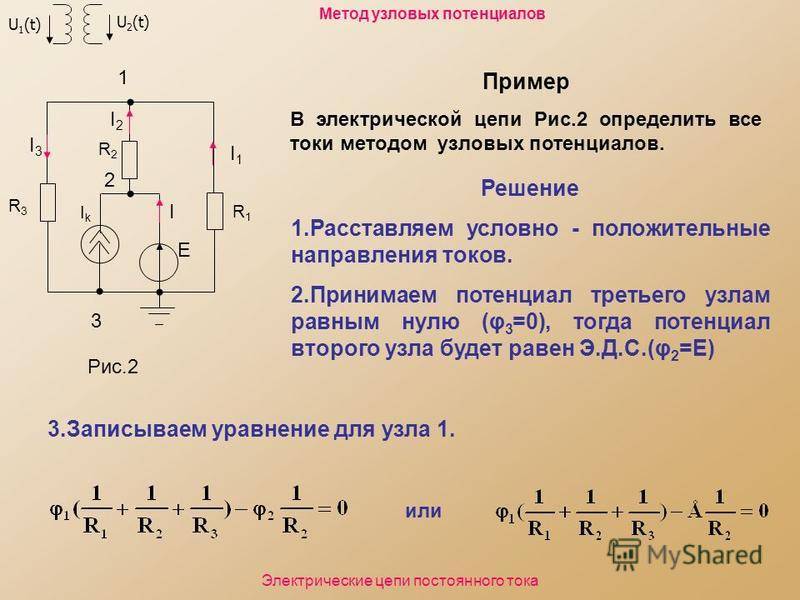
Метод узловых (потенциалов) напряжений

ТОЭ › Методы расчета цепей постоянного тока

При изучении основ электротехники приходится сталкиваться с необходимостью расчета тех или иных параметров различных схем. И самое простое, что приходится делать – это расчет токов ветвей в цепях постоянного тока.

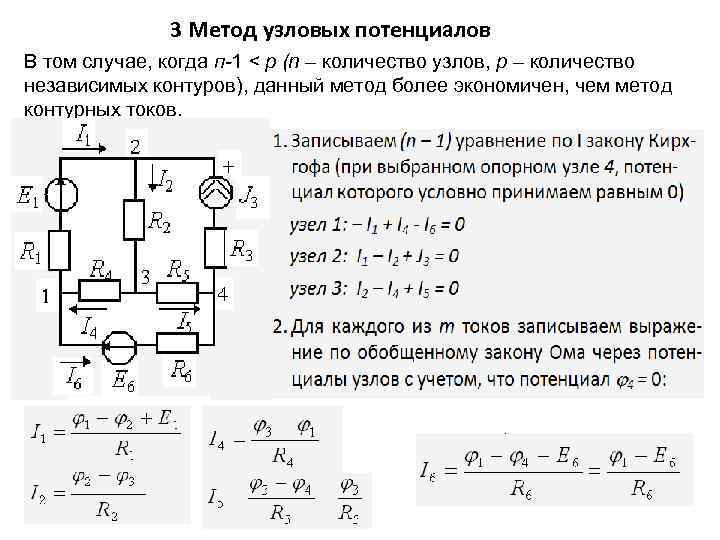
Существует несколько наиболее применяемых методов расчетов для таких цепей: с помощью законов Кирхгофа, методом контурных токов, узловых потенциалов, методом эквивалентного генератора, эквивалентного источника тока, методом наложения. Для расчета более сложных цепей, например, в нелинейных схемах, могут применяться метод аппроксимации, графические методы и другие. В данном разделе рассмотрим один из методов определения токов в цепи постоянного тока – метод узловых потенциалов.

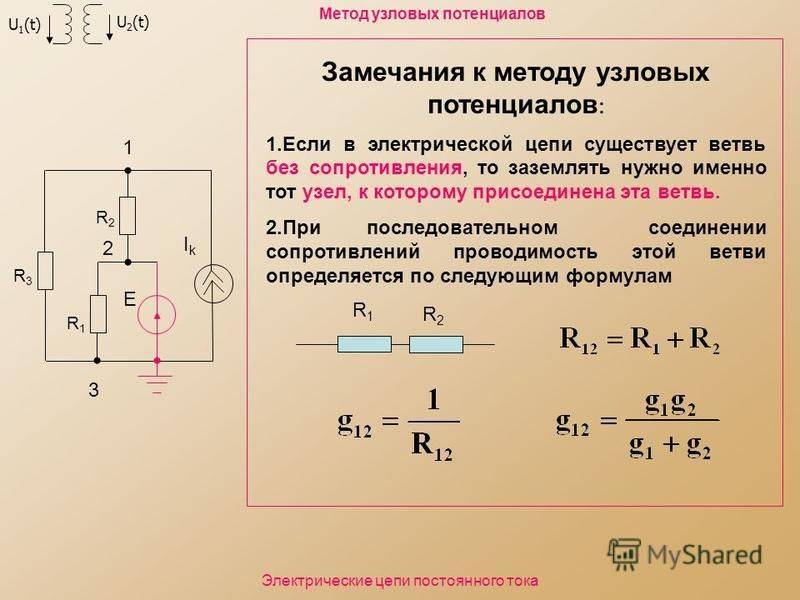
Важно отличать метод узловых напряжений (потенциалов) от метода узлового напряжения (метод двух узлов)

Метод узловых потенциалов примеры решения задач

Для того, чтобы лучше разобраться в этом вопросе, рассмотрим конкретный пример схемы, показанной на рис.1.

Рис.1. Схема постоянного тока

Для начала обозначают направления токов в ветвях. Направление можно выбирать любым. Если в результате вычислений какой-то из токов получится с отрицательным значением, значит, его направление в действительности будет направлено в противоположную сторону относительно ранее обозначенного. Если в ветви имеется источник, то для удобства лучше обозначить направление тока в этой ветви совпадающим с направлением источника в этой ветви, хотя и не обязательно. Далее один из узлов схемы заземляем. Заземленный узел будет называться опорным, или базисным. Такой метод заземления на общее токораспределение в схеме влияния не оказывает.

Какой именно узел заземлять, значения не имеет. Заземлим, например, узел 4 φ4 = 0.

Каждый из этих узлов будет обладать своим значением потенциала относительно узла 4. Именно значения этих потенциалов для дальнейшего определения токов и находят. Соответственно, для удобства этим потенциалам присваивают номера в соответствии с номером узла, т.е. φ1, φ2, φ3. Далее составляется система уравнений для оставшихся узлов 1, 2, 3.

В общем виде система имеет вид:

Использованные в этой системе уравнений буквенно-цифровые обозначения

имеют следующий смысл:

– сумма проводимостей ветвей, сходящихся в узле 1. В данном случае

– сумма проводимостей ветвей, сходящихся в узле 2. В данном случае

– сумма проводимостей ветвей, сходящихся в узле 3. В данном случае

– сумма проводимостей ветвей, соединяющих узлы 1 и 2, взятая со знаком «минус». Для этого единица и взята с отрицательным знаком:

– сумма проводимостей ветвей, соединяющих узлы 1 и 3, взятая со знаком «минус». Для этого единица и в этом случае взята с отрицательным знаком:

Аналогично находятся и остальные проводимости:

J11 – узловой ток узла 1, в котором участвуют ветви, подходящие именно к этому узлу, и содержащие в своем составе ЭДС. При этом, если ЭДС ветви, входящий в узел, направлена к рассматриваемому узлу (в данном случае к узлу 1), то такой узловой ток записывается с плюсом, если от узла, то с минусом. В данном случае

Аналогично

В результате всех ранее приведенных вычисленных значений исходная система уравнений примет вид:

Решать данную систему можно всеми доступными методами, мы же для упрощения решим ее в пакете Mathcad:

В результате получены следующие значения потенциалов в узлах цепи:

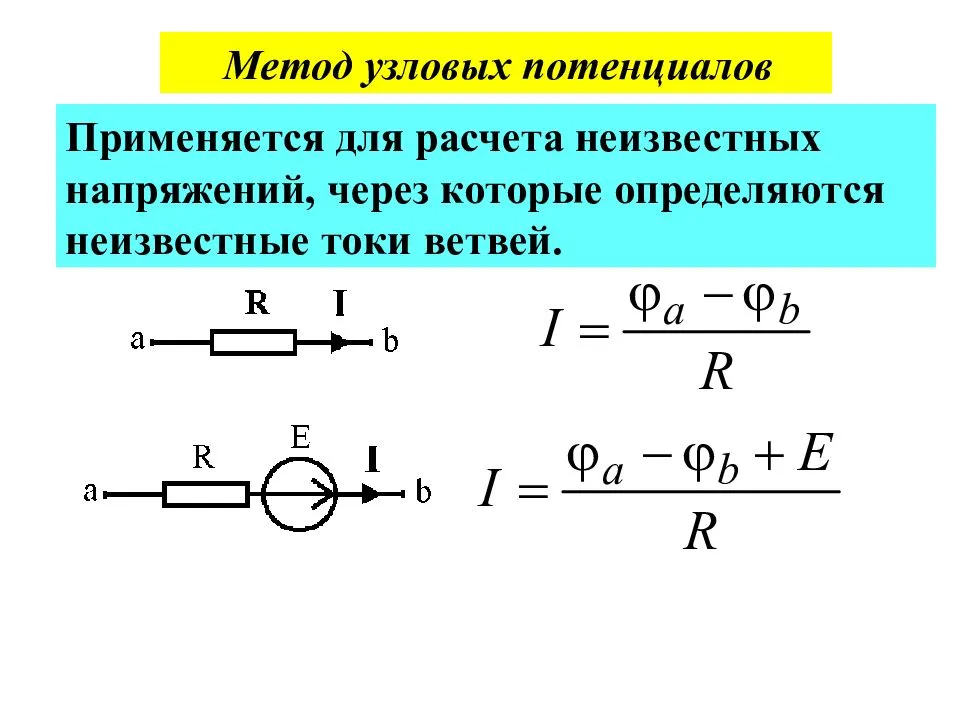
Токи в ветвях находятся в соответствии с законом Ома. Поясним это простыми словами.

В ветви с сопротивлением и источником, учитывая ранее обозначенное направление тока в рассматриваемой ветви, необходимо из потенциала узла, находящегося у начала стрелки направления тока, вычесть потенциал узла, находящегося у конца стрелки направления тока, а затем прибавить значение ЭДС в этой ветви. Далее все это разделить на сопротивление, имеющееся в ветви. Если бы ток и ЭДС в рассматриваемой ветви не совпадали по направлению, тогда значение ЭДС вычиталось. В ветви без ЭДС действует то же самое правило, только ЭДС в числителе, разумеется, отсутствует. В нашем примере получим, что

Значение тока первой ветви, как видно из расчета, получилось отрицательным. Значит, в действительности, этот ток направлен в противоположную сторону относительно его обозначенного направления на рис.1.

Правильность расчетов можно проверить, например, составлением баланса мощностей либо, к примеру, моделированием, схемы. Выполним моделирование в программе Multisim.

Рис.2. Моделирование в Multisim

Как видим, результаты моделирования совпадают с расчетными значениями. Незначительная разница в тысячных долях из-за округлений промежуточных вычислений.

Заказать решение ТОЭ

• Метрология Электрические измерения
• Пигарев А.Ю. РГЗ по электротехнике и электронике в Multisim
• Теория линейных электрических цепей ТЛЭЦ
  • —
    Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи: задание на контрольные работы № 1 и 2 с методическими указаниями для студентов IV курса специальности Автоматика, телемеханика и связь на железнодорожном транспорте
    • —
      Контрольная работа №1
    • —
      Контрольная работа №2
• Электротехника и основы электроники
  • —
    Электротехника и основы электроники: Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений / Соколов Б.П., Соколов В.Б. – М.: Высш. шк., 1985. – 128 с, ил
    • —
      Контрольная работа № 1 Электрические цепи
    • —
      Контрольная работа № 2 Трансформаторы и электрические машины
    • —
      Контрольная работа № 3 Основы электроники
• Теоретические основы электротехники ТОЭ
  • —
    Артеменко Ю.П., Сапожникова Н.М. Теоретические основы электротехники: Пособие по выполнению курсовой работы МГТУ ГА 2009
  • —
    Переходные процессы Переходные процессы в электрических цепях
  • —
    Теоретические основы электротехники Методические указания и контрольные задания для студентов технических специальностей вузов
    • —
      Задание 1 Линейные электрические цепи постоянного и синусоидального тока
      • —
        Задача 1.1 Линейные электрические цепи постоянного тока
      • —
        Задача 1.2 Линейные электрические цепи синусоидального тока
    • —
      Задание 2 Четырехполюсники, трехфазные цепи, периодические несинусоидальные токи, электрические фильтры, цепи с управляемыми источниками
  • —
    Теоретические основы электротехники сб. заданий Р.Я. Сулейманов Т.А. Никитина Екатеринбург УрГУПС 2010
  • —
    Трехфазные цепи. Расчет трехфазных цепей
  • —
    УГТУ-УПИ Решение ТОЭ Билеты по ТОЭ
  • —
    Электромагнитное поле Электростатическое поле Электростатическое поле постоянного тока в проводящей среде Магнитное поле постоянного тока

Задача №1. Дана схема, и известны сопротивления резисторов и ЭДС источников. Требуется найти токи в ветвях, используя законы Кирхгофа.

₁₃₁Задача №2. Задачи для самостоятельного решения:_{1211вн22вн1212121122}Самостоятельная работа №9 Решение задач на расчёт цепей постоянного тока методом узлового напряжения, методом контурных токов и методом наложения токов.Метод узлового напряжения._1231234узловым напряжением_{АБ12312341231141111234}узловое напряжение равно алгебраической сумме произведений ЭДС на проводимости соответствующих ветвей, деленной на сумму проводимости ветвей.2. Метод контурных токов. Контурный ток₁₁₂₂Контурная ЭДССобственным сопротивлением3. Метод наложения_{33313211232123}Примеры решения задачЗадача №1Метод узлового напряжения_212123122Задача 2.Метод контурных токов _{123112233122111 1222}

Элементы цепи

При сравнении внешних характеристик источника ЭДС рис. Мощность трёхфазной цепи 3.

Классический метод расчёта переходных процессов 5. В зависимости от электропроводности все вещества подразделяют на: 1.

Последовательное соединение в цепи Большое количество электрических цепей состоят из нескольких приемников тока.

Согласованный режим Согласованный режим электрической цепи обеспечивает максимальную передачу активной мощности от источника питания к потребителю. На схеме этот элемент выглядит следующим образом. В этой схеме реальные элементы цепи изображаются условными обозначениями, причем вспомогательные элементы цепи обычно не изображаются, а если сопротивление соединительных проводов намного меньше сопротивления других элементов цепи, его не учитывают.

Метод узловых потенциалов

Идеальному источнику тока приписывают внутреннее сопротивление, стремящееся к бесконечно большому значению, и неизменный ток Iк не зависящий от напряжения на его зажимах, равный току коротного замыкания, вследствие чего неограниченное увеличение присоединенной к источнику нагрузки сопровождается теоретически неограниченным возрастанием напряжения и мощности. Электрическая цепь и электрический ток, протекающий по ней, характеризуют электромагнитные процессы при помощи напряжения и силы тока.

Различают два рода тока: 1. Ветвь электрической цепи схемы — участок цепи с одним и тем же током. Последовательное включение источников питания источников ЭДС применяется тогда, когда требуется создать напряжение требуемой величины, а рабочий ток в цепи меньше или равен номинальному току одного источника ЭДС рис. Между узлами 1 и 3 имеются две параллельные ветви с источниками ЭДС Е1 и Е2 , между узлами 2 и 3 также имеются две параллельные ветви с резисторами R1 и R2. Данное устройство работы системы применяется к любому электрическому бытовому прибору.

По этой причине для расчета сложных электрических цепей разработаны более рациональные методы расчета, основные из них рассмотрены ниже. Сопротивление в этой электрической цепи приравнивается к сумме сопротивлений всех проводников системы. При сравнении внешних характеристик источника ЭДС рис. В случае когда у одного приемника энергии сопротивление меньше, через него может пройти больше тока, чем через другие элементы системы.

Классический метод расчёта переходных процессов 5. Стрелка в кружке указывает направление возрастания потенциала внутри источника ЭДС. Электрический ток в такой электрической системе имеет несколько вариантов пути прохождения. Это уравнение является линейным. В состав цепи входят: 1.
Законы Кирхгофа — Теория и задача

Переменный ток.

Переменный синусоидальный ток (или напряжение) задается уравнением: Здесь Im – амплитуда тока. ω – угловая частота, находится как ω = 2⋅π⋅f (обычно в условии задается либо f, либо ω) φ – фаза.

Обычно в задачах условия задают либо в таком формате, либо в действующем значении. Амплитудное больше действующего всегда в √2 раз. Если в условии задано просто значение (например, E1 = 220 В), то это значит, что дано действующее значение.

Если же в условии дано «250⋅sin(314t – 15°), В», то его нужно перевести в действующее комплексное значение.

Про комплексные числа можно подробнее прочитать на нашем сайте.

Для перевода величин к действующим необходимо: ,

Точечка над I означает, что это комплекс.

Чтобы не путать с током, в электротехнике комплексная единица обозначается буквой «j».

Для заданного напряжения имеем:

В решении задач обычно оперируют действующими значениями.

В переменном токе вводятся новые элементы:

Катушка индуктивности	L –
Конденсатор	С –

Их сопротивления (реактивные сопротивления) находятся как: (сопротивление конденсатора — отрицательное)

Например, имеем схему, она подключена на напряжение 200 В, имеющего частоту 100 Гц. Требуется найти ток. Параметры элементов заданы:

Чтоб найти ток, необходимо напряжение разделить на сопротивление (из закона Ома). Здесь основная задача – найти сопротивление. Комплексное сопротивление находится как:

Напряжение делим на сопротивление и получаем ток.

Все эти действия удобно проводить в MathCad. Комплексная единица ставится «1i» или «1j». Если нет возможности, то:

1. Деление удобно производить в показательной форме.
2. Сложение и вычитание – в алгебраической.
3. Умножение – в любой (оба числа в одинаковой форме).

Также, скажем пару слов о мощности. Мощность есть произведение тока и напряжения для цепей постоянного тока. Для цепей переменного тока вводится еще один параметр – угол сдвига фаз (вернее его косинус) между напряжением и током.

Предположим, для предыдущей цепи нашли ток и напряжение (в комплексной форме).

Также мощность можно найти и по другой формуле:

В этой формуле — сопряженный комплекс тока. Сопряженный – значит, что его мнимая часть (та, что с j) меняет свой знак на противоположный (минус/плюс). Re – означает действительная часть (та, что без j).

Это были формулы для активной (полезной) мощности. В цепях переменного тока существует так же и реактивная мощность (генерируется конденсаторами, потребляется – катушками).

Реактивная мощность цепи:

Im – мнимая часть комплексного числа (та, что с j).

Зная реактивную и активную мощность можно подсчитать полную мощность цепи:

Для упрощенного расчета цепей постоянного и переменного тока, содержащих большое число ветвей, пользуются одним из упрощенных методов анализа цепей. Рассмотрим подробнее метод контурных токов.

Метод преобразования электрической цепи

Подключение светодиода через резистор и его расчет

Как определить силу тока в отдельных контурах сложных схем? Для решения практических задач не всегда нужно уточнение электрических параметров на каждом элементе. Чтобы упростить вычисления, используют специальные методики преобразования.

Расчет цепи с одним источником питания

Для последовательного соединения пользуются рассмотренным в примере суммированием электрических сопротивлений:

Rэкв = R1 + R2 + … + Rn.

Контурный ток – одинаковый в любой точке цепи. Проверять его можно в разрыве контрольного участка мультиметром. Однако на каждом отдельном элементе (при отличающихся номиналах) прибор покажет разное напряжение. По второму закону Кирхгофа можно уточнить результат вычислений:

E = Ur1 + Ur2 + Urn.

Параллельное соединение резисторов, схемотехника и формулы для расчетов

В этом варианте в полном соответствии с первым постулатом Кирхгофа токи разделяются и соединяются во входных и выходных узлах. Показанное на схеме направление выбрано с учетом полярности подключенного аккумулятора. По рассмотренным выше принципам сохраняется базовое определение равенства напряжений на отдельных компонентах схемы.

Как найти ток в отдельных ветвях, демонстрирует следующий пример. Для расчета приняты следующие исходные значения:

• R1 = 10 Ом;
• R2 = 20 Ом;
• R3= 15 Ом;
• U = 12 V.

По следующему алгоритму будут определяться характеристики цепи:

базовая формула для трех элементов:

Rобщ = R1*R2*R3/(R1*R2 + R2*R3 + R1*R3.

• подставив данные, вычисляют Rобщ = 10 * 20 * 15 / (10*20 + 20*15 +10*15) = 3000 /(200+300+150) = 4,615 Ом;
• I = 12/ 4,615 ≈ 2,6 А;
• I1 = 12/ 10 = 1,2 А;
• I2 = 12/20 = 0,6 А;
• I3 = 12/15 = 0,8 А.

Как и в предыдущем примере, рекомендуется проверить результат вычислений. При параллельном соединении компонентов должно соблюдаться равенство токов на входе и суммарного значения:

I = 1,2 + 0,6 + 0,8 = 2,6 А.

Если применяется синусоидальный сигнал источника, вычисления усложняются. При включении в однофазную розетку 220V трансформатора придется учитывать потери (утечку) в режиме холостого хода. В этом случае существенное значение имеют индуктивные характеристики обмоток и коэффициент связи (трансформации). Электрическое сопротивление (ХL) зависит от следующих параметров:

• частоты сигнала (f);
• индуктивности (L).

Вычисляют ХL по формуле:

ХL = 2π * f * L.

Чтобы находить сопротивление емкостной нагрузки, подойдет выражение:

Хc = 1/ 2π * f * C.

Следует не забывать о том, что в цепях с реактивными компонентами сдвигаются фазы тока и напряжения.

Расчет разветвленной электрической цепи с несколькими источниками питания

Пользуясь рассмотренными принципами, вычисляют характеристики сложных схем. Ниже показано, как найти ток в цепи при наличии двух источников:

• обозначают компоненты и базовые параметры во всех контурах;
• составляют уравнения для отдельных узлов: a) I1-I2-I3=0, b) I2-I4+I5=0, c) I4-I5+I6=0;
• в соответствии со вторым постулатом Кирхгофа, можно записать следующие выражения для контуров: I) E1=R1 (R01+R1)+I3*R3, II) 0=I2*R2+I4*R4+I6*R7+I3*R3, III) -E2=-I5*(R02+R5+R6)-I4*R4;
• проверка: d) I3+I6-I1=0, внешний контур E1-E2=I1*(r01+R1)+I2*R2-I5*(R02+R5+R6)+I6*R7.

Пояснительная схема к расчету с двумя источниками

Метод расчета по законам Ома и Кирхгофа

До изучения технологий вычислений необходимо уточнить особенности типовых элементов при подключении к разным источникам питания. При постоянном токе сопротивлением индуктивности можно пренебречь. Конденсатор эквивалентен разрыву цепи. Также следует учитывать следующие различия разных видов соединений резисторов:

• последовательное – увеличивает общее сопротивление;
• параллельное – распределяет токи по нескольким ветвям, что улучшает проводимость.

Закон Ома для участка цепи

Дифференциальный автомат надежная защита электрических цепей и человека

Типовая аккумуляторная батарея легкового автомобиля вырабатывает напряжение U = 12 V. Бортовой или внешний амперметр покажет соответствующее значение при измерении. Соединение клемм проводом недопустимо, так как это провоцирует короткое замыкание. Если жила тонкая (< 1 мм), высокая плотность тока в соответствующем поперечном сечении быстро увеличит температуру вплоть до теплового разрушения материала с разрывом цепи. Этот пример демонстрирует функциональность обычного плавкого предохранителя.

Подключив нагрузку, можно мультиметром проверить напряжение. Значение этого параметра остается неизменным. Если известно сопротивление (пример – R = 50 Ом), применение закона Ома (I = U R) поможет рассчитать ток:

I = 12/ 50 = 0,24 А.

По вычисленному значению с использованием формулы быстро определяется мощность:

P = I2 *R = U2/ R = 0,0576 * 50 = 2,88 Вт.

К сведению. Результат показанного расчета пригодится для поиска подходящего резистора. Следует делать запас в сторону увеличения. По стандарту серийных изделий подойдет элемент с паспортной номинальной мощностью 5 Вт.

На практике приходится решать более сложные задачи. Так, при значительной длине линии нужно учесть влияние соединительных ветвей цепи. Через стальной проводник ток будет протекать хуже, по сравнению с медным аналогом. Следовательно, надо в расчете учитывать удельное сопротивление материала. Короткий провод можно исключить из расчета. Однако в нагрузке может быть два элемента. В любом случае общий показатель эквивалентен определенному сопротивлению цепи. При последовательном соединении Rэкв = R1 + R2 +…+ Rn. Данный метод пригоден, если применяется постоянный ток.

Закон Ома для полной цепи

Для вычисления такой схемы следует добавить внутреннее сопротивление (Rвн) источника. Как найти ток, показывает следующая формула:

I = U/ (Rэкв + Rвн).

Вместо напряжения (U) при расчетах часто используют типовое обозначение электродвижущей силы (ЭДС) – E.

Первый закон Кирхгофа

По классической формулировке этого постулата алгебраическая сумма токов, которые входят и выходят из одного узла, равна нулю:

I1 + I2 + … + In = 0.

Это правило действительно для любой точки соединения ветвей электрической схемы. Следует подчеркнуть, что в данном случае не учитывают характеристики отдельных элементов (пассивные, реактивные). Можно не обращать внимания на полярность источников питания, включенных в отдельные контуры.

Чтобы исключить путаницу при работе с крупными схемами, предполагается следующее использование знаков отдельных токов:

• входящие – положительные (+I);
• выходящие – отрицательные (-I).

Второй закон Кирхгофа

Этим правилом установлено суммарное равенство источников тока (ЭДС), которые включены в рассматриваемый контур. Для наглядности можно посмотреть, как происходит распределение контрольных параметров при последовательном подключении двух резисторов (R1 = 50 Ом, R2 = 10 Ом) к аккумуляторной батарее (Uакб = 12 V). Для проверки измеряют разницу потенциалов на выводах пассивных элементов:

• UR1 = 10 V;
• UR1 = 2 V;
• Uакб = 12 V = UR1 + UR2 = 10 + 2;
• ток в цепи определяют по закону Ома: I = 12/(50+10) = 0,2 А;
• при необходимости вычисляют мощность: P = I2 *R = 0,04 * (50+10) = 2,4 Вт.

Второе правило Кирхгофа действительно для любых комбинаций пассивных компонентов в отдельных ветвях. Его часто применяют для итоговой проверки. Чтобы уточнить корректность выполненных действий, складывают падения напряжений на отдельных элементах. Следует не забывать о том, что дополнительные источники ЭДС делают результат отличным от нуля.

Законы Кирхгофа для расчёта электрических цепей

При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие полностью определить режим её работы.

Воспользуйтесь программой онлайн-расчёта электрических цепей.

Прежде чем перейти к самим законам Кирхгофа, дадим определение ветвей и узлов электрической цепи.

Ветвью электрической цепи называется такой её участок, который состоит только из последовательно включённых источников ЭДС и сопротивлений, вдоль которого протекает один и тот же ток. Узлом электрической цепи называется место (точка) соединения трёх и более ветвей. При обходе по соединённым в узлах ветвям можно получить замкнутый контур электрической цепи. Каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза .

Первый закон Кирхгофа

Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна нулю:

∑i = 0,

или в комплексной форме

∑I = 0.

Второй закон Кирхгофа

Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом замкнутом контуре алгебраическая сумма напряжений на сопротивлениях, входящих в этот контур, равна алгебраической сумме ЭДС:

∑Z ∙ I = ∑E.

Количество уравнений, составляемых для электрической цепи по первому закону Кирхгофа, равно Nу – 1, где Nу – число узлов. Количество уравнений, составляемой для электрической цепи по второму закону Кирхгофа, равно Nв – Nу + 1, где Nв – число ветвей. Количество составляемых уравнений по второму закону Кирхгофа легко определить по виду схемы: для этого достаточно посчитать число «окошек» схемы, но с одним уточнением: следует помнить, что контур с источником тока не рассматривается.

Опишем методику составления уравнений по законам Кирхгофа. Рассмотрим её на примере электрической цепи, представленной на рис. 1.

Рис. 1. Рассматриваемая электрическая цепь

Для начала необходимо задать произвольно направления токов в ветвях и задать направления обхода контуров (рис. 2).

Рис. 2. Задание направления токов и направления обхода контуров для электрической цепи

Количество уравнений, составляемых по первому закону Кирхгофа, в данном случае равно 5 – 1 = 4. Количество уравнений, составляемых по второму закону Кирхгофа, равно 3, хотя «окошек» в данном случае 4. Но напомним, что «окошко», содержащее источник тока J1, не рассматривается.

Составим уравнения по первому закону Кирхгофа. Для этого «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» — со знаком «-». Отсюда для узла «1 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

I1 – I2 – I3 = 0;

для узла «2 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

—I1 – I4 + I6 = 0;

для узла «3 у.»:

I2 + I4 + I5 – I7 = 0;

для узла «4 у.»:

I3 – I5 – J1 = 0

Уравнение для узла «5 у.» можно не составлять.

Составим уравнения по второму закону Кирхгофа. В этих уравнениях положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура. Для контура «1 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:

ZC1 ∙ I1 + R2 ∙ I2 – ZL1 ∙ I4 = E1;

для контура «2 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:

-R2 ∙ I2 + R4 ∙ I3 + ZC2 ∙ I5 = E2;

для контура «3 к.»:

ZL1 ∙ I4 + (ZL2 + R1) ∙ I6 + R3 ∙ I7 = E3,

где ZC = — 1/(ωC), ZL = ωL.

Таким образом, для того, чтобы найти искомые токи, необходимо решить следующую систему уравнений:

В данном случае это система из 7 уравнений с 7 неизвестными. Для решения данной системы уравнений удобно пользоваться Matlab. Для этого представим эту систему уравнений в матричной форме:

Для решения данной системы уравнений воспользуемся следующим скриптом Matlab:

>> syms R1 R2 R3 R4 Zc1 Zc2 Zl1 Zl2 J1 E1 E2 E3; >> A = ; >> b = ; >> I = A\b

В результате получим вектор-столбец I токов из семи элементов, состоящий из искомых токов, записанный в общем виде. Видим, что программный комплекс Matlab позволяет существенно упростить решение сложных систем уравнений, составленных по законам Кирхгофа.

Список использованной литературы

1. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.

Рекомендуемые записи

• Метод контурных токов для расчёта электрических цепей При расчёте электрических цепей, помимо законов Кирхгофа, часто применяют метод контурных токов. Метод контурных токов…
• Метод фазных координат: пример расчёта матрицы передачи Расчёт матриц передачи многополюсников различной формы осуществляется достаточно просто. Матрицы передачи — это математическое описание рассматриваемой…

Расчет сложных цепей постоянного тока методом узловых уравнений

Методы расчета сложных электрических цепей постоянного тока 1. Метод узловых и контурных уравнений

В основе расчета лежат первый и второй законы Кирхгофа.

1. Произвольно выбираем направление тока в ветвях.
2. Произвольно выбираем направление обхода контуров.
3. Зная полярность источников, проставляем направление ЭДС.
4. Составляем уравнения по первому закону Кирхгофа. Их должно быть но одно меньше, чем узлов.
5. Составляем уравнения по второму закону Кирхгофа из расчета, что общее число уравнений должно быть равно числу неизвестных токов.
6. Решаем систему уравнений и определяем неизвестные токи. Если в результате решения какой-либо ток окажется со знаком «-», то направление его противоположно выбранному.

1. 1=r2=0;
2. 1=0,3 Ом;
3. 2=1 Ом;
4. 3=24 Ом;

Итак, на схеме рисуем направления токов (1), согласно этим направлениям рисуем направления обхода контуров (2), согласно полярности источников питания ставим направления ЭДС (3).

Согласно первому закону Кирхгофа:

Теперь составляем уравнения по второму закону Кирхгофа:

Получили систему из трех уравнений. Решаем.

2. Метод контурных токов

Этот метод основан на втором законе Кирхгофа

1. Произвольно выбираем направления контурных токов (рис.2)
2. Составляем уравнения по второму закону Кирхгофа.

3. Определяем истинные токи.

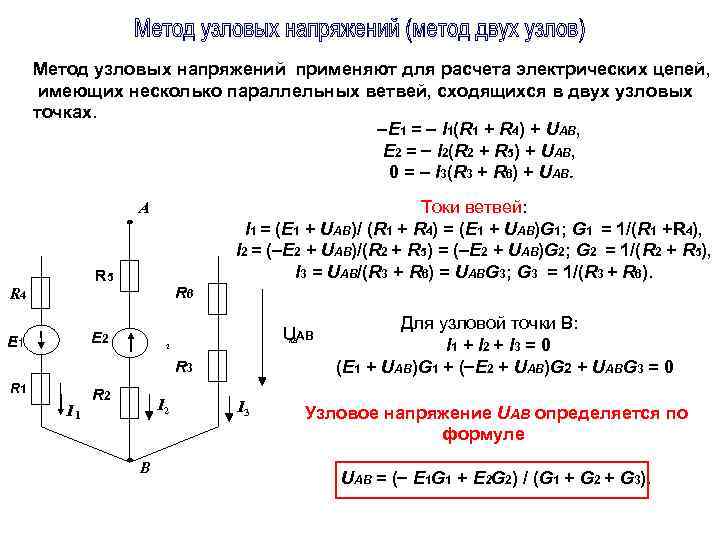
3. Метод двух узлов

Этот метод применим для схем, имеющих два узла

1. Выбираем произвольно направления токов в ветвях в одну и ту-же сторону (см. рис.3 – стрелки со штрихами).
2. Определяем проводимости ветвей:

1. Определяем напряжение между двумя узлами по формуле:

1. Определяем токи в ветвях

Так как, значения I2 и I3 получились отрицательными, то эти токи будут противоположными по направлению (на рисунке показаны жирные сплошные стрелки).

4. Метод наложения или метод суперпозиции

Метод основан на том, что любой ток в цепи создается совместным действием всех источников питания. Поэтому можно рассчитать частичные токи от действия каждого источника питания отдельно, а затем, найти истинные токи как арифметическую составляющую частичных.

Источник

Метки

• алгоритм расчет цепей при несинусоидальных периодических воздействиях
• алгоритм расчета цепей периодического несинусоидального тока
• баланс мощностей
• ВАХ нелинейного элемента
• Векторная диаграмма
• ветви связи
• взаимная индуктивность
• взаимная проводимость
• вольт-амперная характеристика нелинейного элемента
• второй закон Кирхгофа
• второй закон Кирхгофа для магнитных цепей
• входная проводимость
• гармоники напряжения
• гармоники тока
• Генератор напряжения
• генератор тока
• главные контуры
• графический метод расчета нелинейных электрических цепей
• динамическое сопротивление
• дифференциальное сопротивление
• емкость двухпроводной линии
• емкость коаксиального кабеля
• емкость конденсатора
• емкость однопроводной линии
• емкость плоского конденсатора
• емкость цилиндрического конденсатора
• закон Ампера
• закон Био Савара Лапласа
• закон Ома
• закон полного тока
• закон электромагнитной индукции
• Законы Кирхгофа
• индуктивность
• индуктивность двухпроводной линии
• индуктивность однопроводной линии
• индуктивность соленоида
• катушка со сталью
• Конденсатор в цепи постоянного тока
• контурные токи
• коэффициент амплитуды
• коэффициент гармоник
• коэффициент искажения
• коэффициент магнитной связи
• коэффициент мощности трансформатора
• коэффициент трансформации
• коэффициент формы
• кусочно-линейная аппроксимация
• магнитная постоянная
• магнитная цепь
• магнитный поток рассеяния
• метод активного двухполюсника
• метод двух узлов
• метод контурных токов
• метод наложения
• метод узловых напряжений
• метод узловых потенциалов
• метод эквивалентного генератора
• метод эквивалентного источника ЭДС
• Метод эквивалентных преобразований
• методы расчета магнитных цепей
• независимые контуры
• нелинейный элемент
• несинусоидальный периодический ток
• обобщенный закон Ома
• опорный узел
• основной магнитный поток
• параллельное соединение конденсаторов
• первый закон Кирхгофа
• первый закон Кирхгофа для магнитных цепей
• последовательное соединение конденсаторов
• последовательный колебательный контур
• постоянная составляющая тока
• потери в меди
• потери в стали
• приведенный трансформатор
• Примеры расчета схем при несинусоидальных периодических воздействиях
• принцип взаимности
• принцип компенсации
• расчет гармоник тока
• расчет магнитной цепи
• расчет нелинейных цепей постоянного тока
• расчет цепей несинусоидального тока
• Расчет цепи конденсаторов
• расчет цепи с несинусоидальными периодическими источниками
• Резонанс в электрической цепи
• решение задач магнитные цепи
• сила Ампера
• сила Лоренца
• Символический метод
• собственная проводимость
• статическое сопротивление
• сферический конденсатор
• теорема об эквивалентном источнике
• теорема Тевенена
• топографическая диаграмма
• Трансформаторы
• трехфазная система
• удельная энергия магнитного поля
• уравнения трансформатора
• Цепи с конденсаторами
• частичные токи
• чередование фаз
• ЭДС самоиндукции
• эквивалентная схема трансформатора
• электрическая постоянная
• электроемкость
• энергия магнитного поля