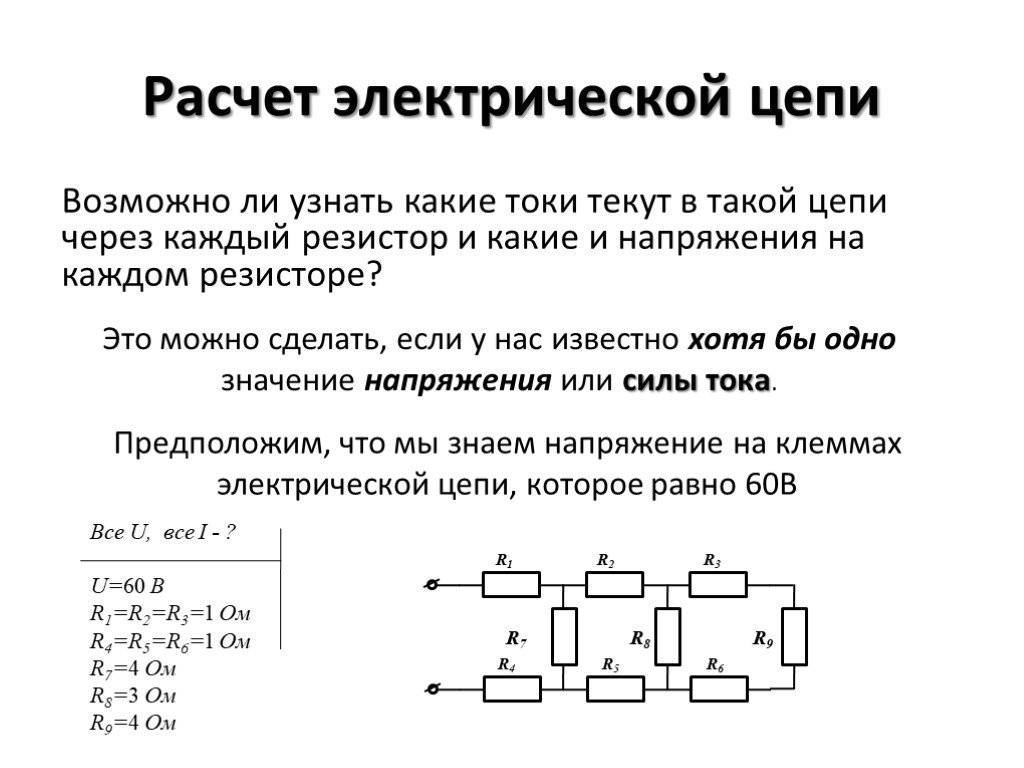
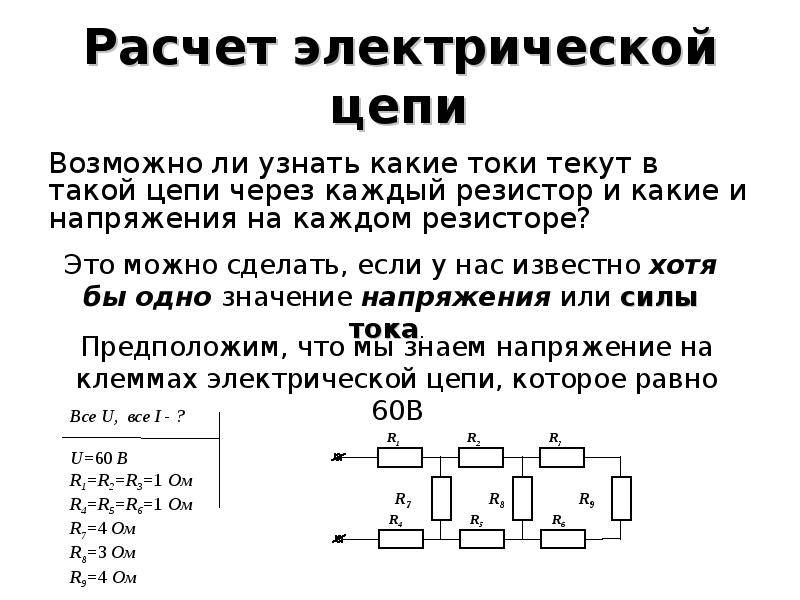
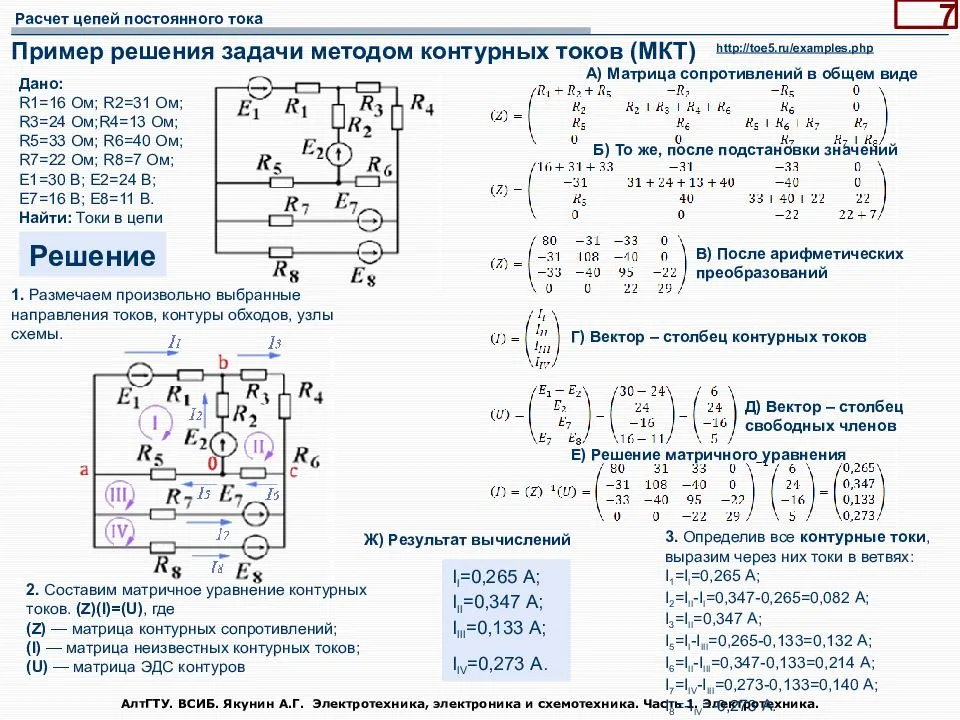
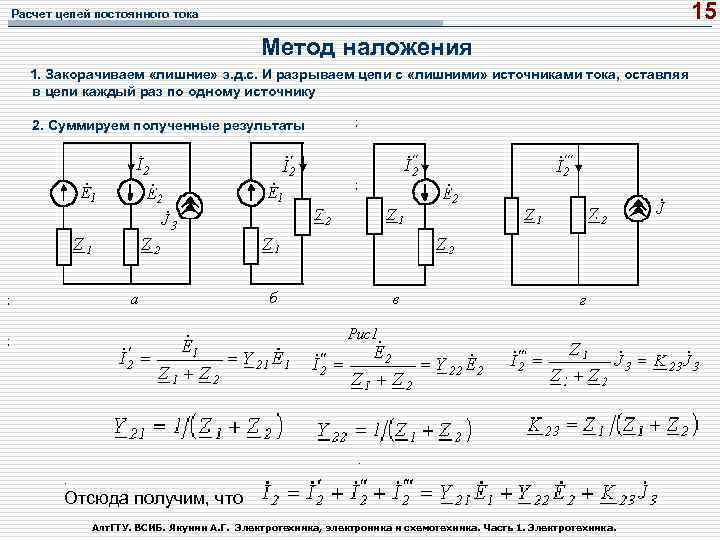
Сила тока и закон Ома
Осуществляя расчет силы тока цепи, следует помнить, что эта величина физического типа, демонстрирующая определенный заряд. Он протекает за некоторую временную единицу по проводнику. Базовая схема вычисления следующая:
I=q/t, где:
- I – сила электричества в Амперах (А) или Кл/с;
- q – заряд, перемещающийся в рамках проводника в Кулонах (Кл);
- t – время, затраченное на перемещение заряда, с.
В соответствии с положениями закона Ома для отдельной части цепи при вычислении силы тока применяется схема, показывающая:
- прямую зависимость силы тока от напряжения;
- взаимосвязь обратного типа с сопротивлением.
I=U/R, где:
- U – выраженное в вольтах напряжение, В;
- R – показатель сопротивления, Ом.
Отсюда будет следовать такая зависимость:
I = E/ R+r, где:
- Е – ЭДС, В;
- R – сопротивление внешнего типа, Ом
- r – сопротивление внутреннее, Ом
Воспользуйтесь другими онлайн калькуляторами:
Ток, протекающий в цепи параллельно соединенных резисторах
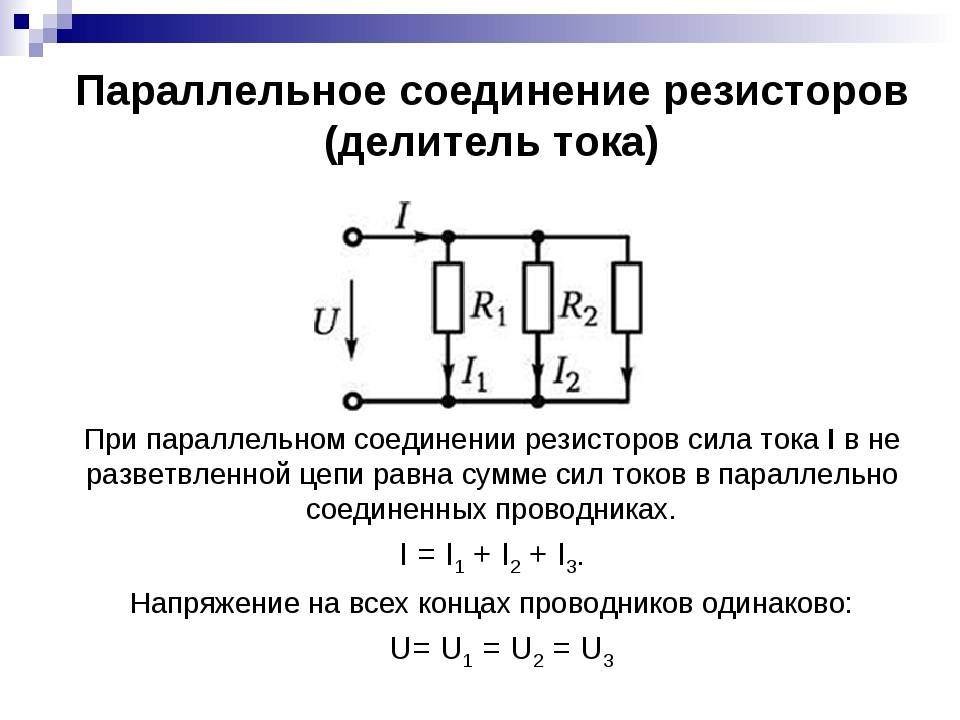
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (закон Ома для участка цепи).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Таким образом, протекающий общий ток в цепи можно определить как:
I = I1 + I2
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Как узнать свою схему
Для правильного определения и расчета мощности требуется знание нескольких факторов:
- Количества фаз питания;
- Способа соединения потребителей.
При однофазном подключении используется два провода:
- Фазный провод;
- Нулевой провод.
Для трехфазной сети характерно наличие трех или четырех проводников (подключение с заземленной нейтралью). При этом используется две различных схемы включения:
- «Треугольник». Каждая нагрузка подсоединяется с двумя соседними. Напряжение каждой фазы подводится к точкам соединения потребителей.
- «Звезда». Все три потребителя соединяются в одной точке. Ко вторым концам подключаются фазы питания. Это схема с изолированной нейтралью. В схеме с заземленной нейтралью точка соединения потребителей подключается к нулевому проводнику.
Соединение источника и потребителей
Закон Ома для цепи переменного тока
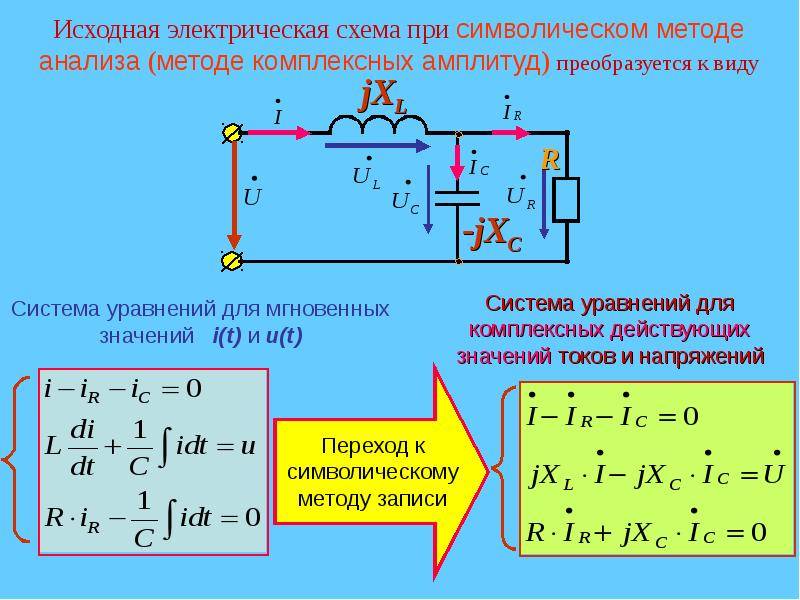
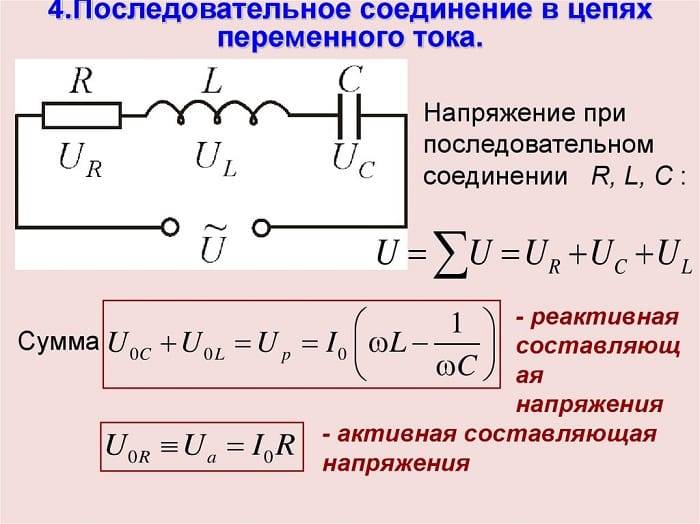
В цепи переменного тока сопротивление кроме активной, может иметь как емкостную, так и индуктивную составляющие. Рассмотрим цепь переменного тока, состоящую из резистора сопротивлением R, конденсатора емкостью C и катушки индуктивностью L, соединенных последовательно.

Мгновенные значения силы тока на всех элементах этой цепи одинаковы, а мгновенное значение напряжения между концами цепи равно алгебраической сумме мгновенных значений напряжений на резисторе (UR), конденсаторе (UC) и катушке индуктивности (UL).
Для того чтобы определить амплитудные (или действующие) значения напряжения и силы тока, а также сдвиг фаз между ними удобно использовать метод векторных диаграмм. Здесь действующие значения всех напряжений и токов рассматриваются как векторы, вращающиеся с угловой скоростью ω, равной циклической частоте переменного тока, а их мгновенные значения определяются проекциями этих векторов на горизонтальную ось. Так как сила тока в цепи одинакова, то построение векторной диаграммы начинается с вектора I¯0, модуль которого равен амплитудному значению силы тока в цепи. Направление этого вектора может быть любым. Зададим угол α = ωt к горизонтали.

Колебания напряжения на активном сопротивлении совпадают по фазе с колебаниями силы тока, поэтому вектор U¯0R, модуль которого равен U0R = I0 × R, совпадает по направлению с вектором I¯0. Сдвиг фаз между колебаниями силы тока и колебаниями напряжения на индуктивном сопротивлении составляет π / 2, причем ток отстает по фазе от напряжения. Поэтому вектор U¯0L, модуль которого равен U0L = I0 × ωL, нужно повернуть относительно вектора I¯0 на угол π / 2 против часовой стрелки. Вектор U¯0C, модуль которого равен I0 / ωC, отстает по фазе от вектора I¯0 на π / 2, поэтому его нужно повернуть на этот угол по часовой стрелке.
Для того чтобы найти напряжение на зажимах цепи, необходимо сложить три вектора: U¯0 = U¯0R + U¯0L + U¯0C.
В первую очередь сложим векторы U¯0R и U¯0C. Модуль этой суммы U’0 = . Пусть ωL > 1 / ωC, тогда: U’0 = I0 × (ωL — 1 / ωC).
Теперь сложим векторы U¯0R и U’¯0. Модуль вектора U¯0 определяется по теореме Пифагора: U0² = U0R² + (U0L — U0C)² = I0² × R² + I0² × (ωL — 1 / ωC)². Соответственно амплитудное (действующее) значение силы тока в цепи переменного тока равно отношению амплитудного (действующего) значения напряжения на концах этой цепи к его полному сопротивлению (закон Ома для цепи переменного тока):
I0 = U0 / √(R² + (ωL — 1 / ωC)²) = U0 / Z, где:
- Z — полное сопротивление (импеданс) цепи.
- R — его активное сопротивление.
- ωL — 1 / ωC — реактивное сопротивление цепи переменного тока.
- ω = 2 × π × γ — циклическая, угловая частота. γ — частота переменного тока.
Сдвиг фаз между силой тока и напряжением равен углу φ между векторами U¯0 и I¯0. В соответствии с графиком выше ток отстает от напряжения на угол φ, причем tgφ = (ωL — 1 / ωC) / R.
Для того чтобы определить мгновенные значения напряжений на активном, емкостном и индуктивном сопротивлениях, необходимо спроектировать векторы U¯0R, U¯0L, U¯0C на прямую АВ.

Тогда:
- UR = I0 × R × sin × (ωt + φ).
- UL = I0 × ωL × sin × (ωt + φ + π / 2).
- UC = (I0 / ωС) × sin × (ωt + φ — π / 2).
Если 1 / ωС > ωL, то:
- U’0 = I0 × (1 / ωС — ωL).
- tgφ = (1 / ωC — ωL) / R, причем ток опережает напряжение по фазе на угол φ.
Поддерживаемые расширения и настраиваемые параметры
Попробуйте её именно сегодня! Графический редактор от Майкрософт — Visio Для тех, кто имеет хоть небольшой опыт работы с продуктами Майкрософт, освоить работу в из графическом редакторе Visio Визио будет несложно.
Он был способным к моделированию. Это кросс-платформенная программа, и она работает на Mac и Windows.
Данный софт поддерживает не только работу в плоскости, но и позволяет создавать полноценные 3D-модели.
Вы можете изменить форматы по вашему желанию. Micro-Cap — одно из лучших приложений для моделирования электросети Программа позволяет установить зависимость параметров номиналов элементов от температурного режима, освещенности, частотных характеристик и т. Проверить операцию через симулятор электроцепи.
Платные приложения
Мы также рекомендуем пользователям поделиться своими отличными дизайнами в разделе электрических схем нашего сообщества. Встроенные примеры принципиальной электрической схемы Перед созданием схемы, многие люди хотят смотреть некоторе хорошие примеры. Он имеет очень простое и понятное устройство, так что через час-полтора работы вы будете уже свободно ориентироваться. Во втором редакторе создаются печатные платы.
Простой интерфейс Интерфейс пользователя достаточно простой и аккуратно организованный. Разработчикам не удалось повысить качество и увеличить графический интерфейс пользователя. Редактор реализован достаточно удобно.
Бесплатные
Редактор реализован достаточно удобно. Для использования различными специалистами графический редактор пополняется дополнительными модулями. Большое количество инструментов сформировано по группам и удобно настраивается под конкретные условия чертежа. Для редактирования изображений используется масштабирование, работа с окнами и слоями, перемещение, вставка разрывов, вращение, изменение отражения, наложение текста, цветовая палитра и другие функции и стили.
Что приятно, что можно легко менять масштаб — прокруткой колеса мышки. Здесь добавляются и редактируются компоненты.
Рисование электрических схем в программе Microsoft Word
калькулятор электрических цепей онлайн
Вы искали калькулятор электрических цепей онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и онлайн калькулятор электрических цепей, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «калькулятор электрических цепей онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как калькулятор электрических цепей онлайн,онлайн калькулятор электрических цепей,онлайн расчет цепей,онлайн расчет цепей постоянного тока,онлайн расчет цепи,онлайн расчет цепи переменного тока,онлайн расчет цепи постоянного тока,онлайн расчет электрических схем,онлайн расчет электрических цепей,онлайн расчет электрической цепи,онлайн составление электрических схем,онлайн упрощение электрических цепей,онлайн цепь электрическая,онлайн электрическая цепь,онлайн электрические цепи,построение электрических цепей онлайн,построить электрическую цепь онлайн,рассчитать цепь электрическую,рассчитать электрическую цепь,расчет линейной цепи постоянного тока онлайн,расчет схем электрических онлайн,расчет цепей онлайн,расчет цепей постоянного тока онлайн,расчет цепи онлайн,расчет цепи переменного тока онлайн,расчет цепи постоянного тока онлайн,расчет электрических схем онлайн,расчет электрических цепей онлайн,расчет электрической цепи онлайн,схема онлайн электрическая,упрощение электрических цепей онлайн,электрическая цепь онлайн,электрические цепи онлайн. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и калькулятор электрических цепей онлайн. Просто введите задачу в окошко и нажмите
«решить» здесь или введите в окно ввода ниже свой запрос (например, онлайн расчет цепей).
Расчёт величины тока по мощности и напряжению
Для обеспечения безопасности при эксплуатации бытовых электроприборов необходимо верно вычислить сечение питающего кабеля и проводки. Поскольку ошибочно выбранное сечение жил кабеля способно привести к возгоранию проводки из-за короткого замыкания. Это грозит возникновением пожара в здании. Это также относится к выбору кабеля для подключения электрических двигателей.
Расчет тока
- От значения этой величины зависит выбор питающего кабеля (провода), по которому могут быть подключены приборы электропотребления к сети.
- Зная напряжение электрической сети и полную нагрузку электроприборов, можно по формуле вычислить силу тока, который потребуется пропускать по проводнику (проводу, кабелю). По его величине выбирают площадь сечения жил.
Если известны электропотребители в квартире или доме, необходимо выполнить несложные расчёты, чтобы правильно смонтировать схему электроснабжения.
Однофазная сеть напряжением 220 В
Сила тока I (в амперах, А) подсчитывается по формуле:
I = P / U,
где P – электрическая полная нагрузка (обязательно указывается в техническом паспорте устройства), Вт (ватт);
U – напряжение электрической сети, В (вольт).
Ниже в таблице представлены величины нагрузки типичных бытовых электроприборов и потребляемый ими ток (для напряжения 220 В).
| Электроприбор | Потребляемая мощность, Вт | Сила тока, А |
| Стиральная машина | 2000 – 2500 | 9,0 – 11,4 |
| Джакузи | 2000 – 2500 | 9,0 – 11,4 |
| Электроподогрев пола | 800 – 1400 | 3,6 – 6,4 |
| Стационарная электрическая плита | 4500 – 8500 | 20,5 – 38,6 |
| СВЧ печь | 900 – 1300 | 4,1 – 5,9 |
| Посудомоечная машина | 2000 — 2500 | 9,0 – 11,4 |
| Морозильники, холодильники | 140 — 300 | 0,6 – 1,4 |
| Мясорубка с электроприводом | 1100 — 1200 | 5,0 — 5,5 |
| Электрочайник | 1850 – 2000 | 8,4 – 9,0 |
| Электрическая кофеварка | 6з0 — 1200 | 3,0 – 5,5 |
| Соковыжималка | 240 — 360 | 1,1 – 1,6 |
| Тостер | 640 — 1100 | 2,9 — 5,0 |
| Миксер | 250 — 400 | 1,1 – 1,8 |
| Фен | 400 — 1600 | 1,8 – 7,3 |
| Утюг | 900 — 1700 | 4,1 – 7,7 |
| Пылесос | 680 — 1400 | 3,1 – 6,4 |
| Вентилятор | 250 — 400 | 1,0 – 1,8 |
| Телевизор | 125 — 180 | 0,6 – 0,8 |
| Радиоаппаратура | 70 — 100 | 0,3 – 0,5 |
| Приборы освещения | 20 — 100 | 0,1 – 0,4 |
На рисунке представлена схема устройства электроснабжения квартиры при однофазном подключении к сети напряжением 220 В.
Как видно из рисунка, различные потребители электроэнергии подключены через соответствующие автоматы к электросчётчику и далее общему автомату, который должен быть рассчитан на нагрузку приборов, которыми будет оборудована квартира. Провод, который подводит питание также должен удовлетворять нагрузке энергопотребителей.
Ниже приводится таблица для скрытой проводки при однофазной схеме подключения квартиры для подбора провода при напряжении 220 В
| Сечение жилы провода, мм2 | Диаметр жилы проводника, мм | Медные жилы | Алюминиевые жилы | ||
| Ток, А | Мощность, Вт | Ток, А | Мощность, кВт | ||
| 0,50 | 0,80 | 6 | 1300 | ||
| 0,75 | 0,98 | 10 | 2200 | ||
| 1,00 | 1,13 | 14 | 3100 | ||
| 1,50 | 1,38 | 15 | 3300 | 10 | 2200 |
| 2,00 | 1,60 | 19 | 4200 | 14 | 3100 |
| 2,50 | 1,78 | 21 | 4600 | 16 | 3500 |
| 4,00 | 2,26 | 27 | 5900 | 21 | 4600 |
| 6,00 | 2,76 | 34 | 7500 | 26 | 5700 |
| 10,00 | 3,57 | 50 | 11000 | 38 | 8400 |
| 16,00 | 4,51 | 80 | 17600 | 55 | 12100 |
| 25,00 | 5,64 | 100 | 22000 | 65 | 14300 |
Трёхфазная сеть напряжением 380 В
При трёхфазном электроснабжении сила тока I (в амперах, А) вычисляется по формуле:
I = P /1,73 U,
где P -потребляемая мощность, Вт;
U — напряжение в сети, В,
так как напряжение при трёхфазной схеме электроснабжения 380 В, формула примет вид:
I = P /657, 4.
В случае подведения к дому трёхфазного электроснабжения напряжением 380 В схема подключения будет выглядеть следующим образом.
Сечение жил в питающем кабеле при различной нагрузке при трёхфазной схеме напряжением 380 В для скрытой проводки представлена в таблице.
| Сечение жилы провода, мм2 | Диаметр жилы проводника, мм | Медные жилы | Алюминиевые жилы | ||
| Ток, А | Мощность, Вт | Ток, А | Мощность, кВт | ||
| 0,50 | 0,80 | 6 | 2250 | ||
| 0,75 | 0,98 | 10 | 3800 | ||
| 1,00 | 1,13 | 14 | 5300 | ||
| 1,50 | 1,38 | 15 | 5700 | 10 | 3800 |
| 2,00 | 1,60 | 19 | 7200 | 14 | 5300 |
| 2,50 | 1,78 | 21 | 7900 | 16 | 6000 |
| 4,00 | 2,26 | 27 | 10000 | 21 | 7900 |
| 6,00 | 2,76 | 34 | 12000 | 26 | 9800 |
| 10,00 | 3,57 | 50 | 19000 | 38 | 14000 |
| 16,00 | 4,51 | 80 | 30000 | 55 | 20000 |
| 25,00 | 5,64 | 100 | 38000 | 65 | 24000 |
Для расчёта тока в цепях питания нагрузки, характеризующейся большой реактивной полной мощностью, что характерно применению электроснабжения в промышленности:
- электрические двигатели;
- дроссели приборов освещения;
- сварочные трансформаторы,;
- индукционные печи.
На практике принято считать, что при подсчёте электрических нагрузок для бытовых целей запас мощности принимают 5%. В случае расчёта электрических сетей для промышленного производства запас мощности принимают 20%.
Это интересно: Санузел в деревянном доме – сделать туалет своими руками с канализацией — что важно знать
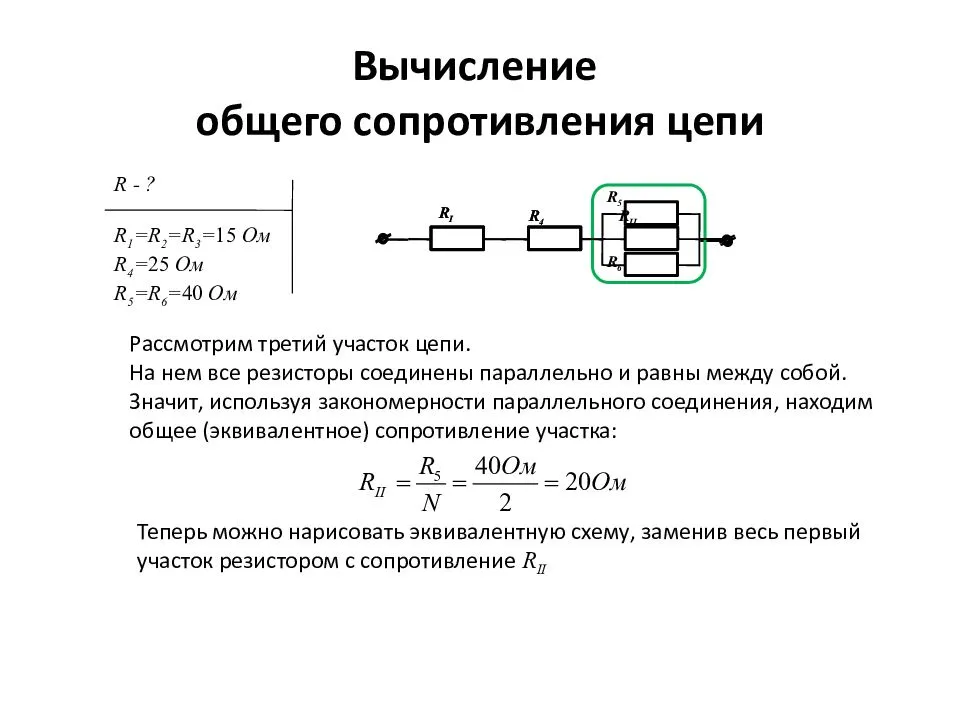
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Запись закона Джоуля-Ленца
Формулировка уравнения Джоуля-Ленца следующая: количество теплоты Q, которое выделилось за единицу времени t на участке цепи, прямо пропорционально произведению сопротивления R на квадрат силы тока I, протекающей через этот участок. Формула закона Джоуля-Ленца имеет вид: Q = a * sqr (I) * R * t. Литера «а» является температурным коэффициентом, который равен 1 при условии, что количество теплоты получается в джоулях. Если принять его равным 0,24, то результат будет измеряться в калориях. Поскольку а = 1, то формула Ленца будет выражаться кратко в таком виде: Q = sqr (I) * R * t.
При перегреве проводника может возникнуть короткое замыкание, которое приводит к выходу аппаратуры из строя. Оно может также быть причиной пожара. Для избежания таких ситуаций в электротехнике применяются плавкие предохранители, которые позволяют прекратить подачу электричества на устройство.
Закон позволяет найти необходимые параметры электрического тока, чтобы избежать перегрева и пожара. Основные соотношения для расчета составляющих величин закона в цепях постоянного тока следующие:
- Закон Ома для участка и полной цепи: I = U / R и i = e / (R + Rвн).
- Q = U * I * t.
- Q = e * i * t.
- Q = (t * sqr (U)) / R.
- Q = (t * sqr (e)) / (R + Rвн).
- Q = P * t.
Различие математической записи закона в цепях с переменным и постоянным токами обусловлено их свойствами и параметрами, а также появлением нагрузок активной и реактивной составляющей. Кроме того, ток переменной составляющей постоянно изменяется во времени. Основные соотношения:
- Закон Ома: i = U / Z, где Z — полное сопротивление цепи. Оно включает в себя активную, индуктивную и емкостную нагрузки.
- Q = S * t = t * .
- Q = U * i * t, где U и i — действующие значения напряжения и тока, которые измеряются при помощи вольтметра и амперметра соответственно. Формулу в таком виде можно применять для примерного расчета Q, причем в цепях, состоящих только из активной нагрузки.
- Запись закона с учетом в электрической цепи активной и реактивной нагрузок: Q = sqr (i) * Z * t.
Примеров применения уравнения Джоуля-Ленца достаточно много, одним из которых является обыкновенная лампа накаливания с вольфрамовой нитью. Свечение происходит из-за высокого напряжения и материала, из которого изготовлена нить накаливания. Электродуговая сварка работает тоже по этому закону, поскольку ток проходит через электрод и оказывает на него тепловое действие, при котором образуется сварочная дуга. Благодаря закону, можно правильно рассчитать и сделать вывод о применении радиокомпонента в какой-либо схеме.
Таким образом, уравнение Джоуля-Ленца играет важную роль в электротехнике, поскольку позволяет произвести точные расчеты радиокомпонентов схемы, исключая перегрев деталей и пожар.
Электрические цепи и их разновидности
Электрическая цепь представляет собой комплекс устройств и отдельных объектов, которые связываются заданным способом. Они обеспечивают путь для прохождения электротока. Для характеристики отношения заряда, протекающего в рамках каждого отдельного проводника за некоторое время, к продолжительности этого времени используется определенная физическая величина. И это сила тока в электрической цепи.
В состав такой цепи включены источник энергии, энергопотребители, т.е. нагрузка и провода. Они делятся на две разновидности:
- Неразветвленные – ток, движущийся от генератора к энергопотребителю, не меняется по своему значению. Например, это освещение, включающее в свой состав только одну лампочку.
- Разветвленные – цепи, имеющие некоторые ответвления. Ток, двигаясь от источника, разделяется и идет на нагрузку по нескольким ветвям. При этом его значение меняется.
Примером может служить освещение, включающее многорожковую люстру.
Ветвь являет собой один или несколько компонентов, соединенных последовательно. Движение тока идет от узла с высоким напряжением к узлу с минимальным его значением. При этом входящий ток на узле совпадает с выходящим.
Цепи могут быть нелинейными и линейными. Если в первых существует один и более элементов, где есть зависимость значений от тока и напряжения, то у вторых характеристики элементов не имеют такой зависимости. Кроме того, в цепях, характеризующихся постоянным током, его направление не меняется, а при условии переменного тока происходит его изменение с учетом параметра времени .
Практическое применение
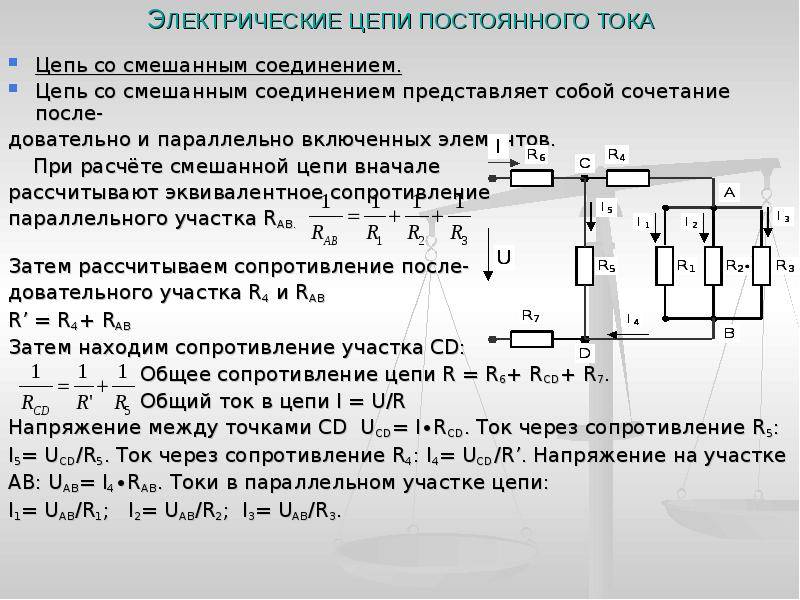
Чаще всего на практике расчёт общего сопротивления цепи выполняют для того, чтобы узнать потребляемую мощность той или иной схемы. При этом, зная общее сопротивление, можно найти и такие важные параметры цепи, как ток и напряжение. Поэтому и рисуют эквивалентную схему электрической цепи. Простые цепи состоят только из последовательных или параллельных участков, но чаще встречаются комбинированные соединения.
Перед тем как приступить к расчёту эквивалентного сопротивления, вся электрическая цепь разделяется на простые контуры. Как только импеданс каждого такого контура будет подсчитан, схема перерисовывается, но вместо контуров рисуется уже резистор. Затем всё повторяется, и это происходит до тех пор, пока не останется один элемент.
Простое соединение
Пусть будет дана схема, состоящая из трёх резисторов, включённых последовательно. При этом сопротивление R1и R2 одинаковое и равно 57 Ом, а сопротивление R3 составляет один килоОм. Для расчёта общего сопротивления цепи сначала понадобится привести значение R3 согласно Международной системе единиц.
R3 = 1 кОм = 1000 Ом.
Так как соединение последовательное, используется формула: Ro = R1+R2+R3. Подставив известные значения, рассчитывается эквивалентное значение: Ro = 57+57+1000 = 1114 Ом.
Если же те же самые резисторы будут расположены параллельно друг другу, то для расчёта общего сопротивления уже используется другое выражение:
1/Ro = 1/R1 + 1/R2 +1/R3.
Ro = R1*R2*R3 / (R1*R2+R2*R3+R1*R3).
Подставив исходные данные в эту формулу, получим:
Ro = 57*57*1000/ (57*57 +57*1000+ 57*1000) = 3249000/117249 = 27,7 Ом.
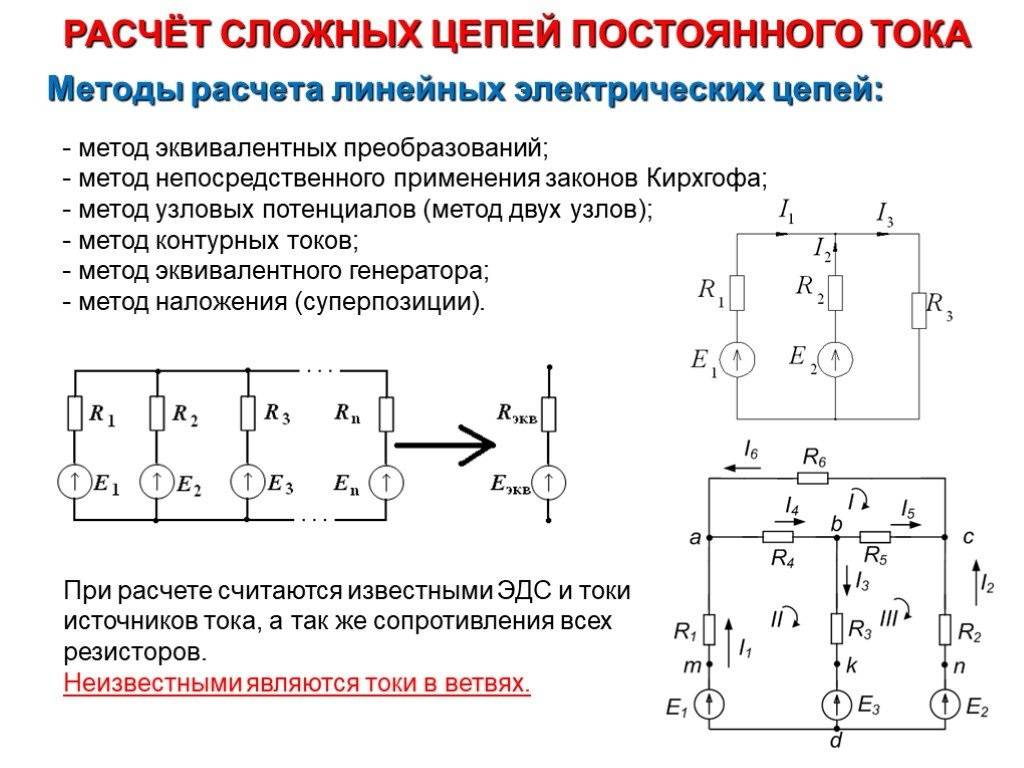
Определение и суть метода контурных токов
Векторная диаграмма токов и напряжений
По данному методу в исследуемой цепи выделяются независимые плоские замкнутые контуры, включающие все, без исключения, элементы. Предполагается, что в каждом контуре может протекать некоторый контурный ток. В том случае, если цепь с элементом принадлежит только одному контуру, то ток через входящие в нее элементы равен контурному. Если элемент охватывается несколькими контурами, то он в ней равен алгебраической (с учетом направления) сумме контурных токов.
Важно! Суммирование должно производиться строго с учетом направления движения при обходе контура. Знак «плюс» – при совпадении направления, «минус» – при противоположном
При составлении уравнений учитываются входящие в схему источники ЭДС и тока.
На пpaктике удобнее преобразовать идеальный источник тока в идеальный источник ЭДС. Преобразование выполняется согласно закона Ома:
U=I∙r, где r – внутреннее сопротивление источника тока (напряжения).
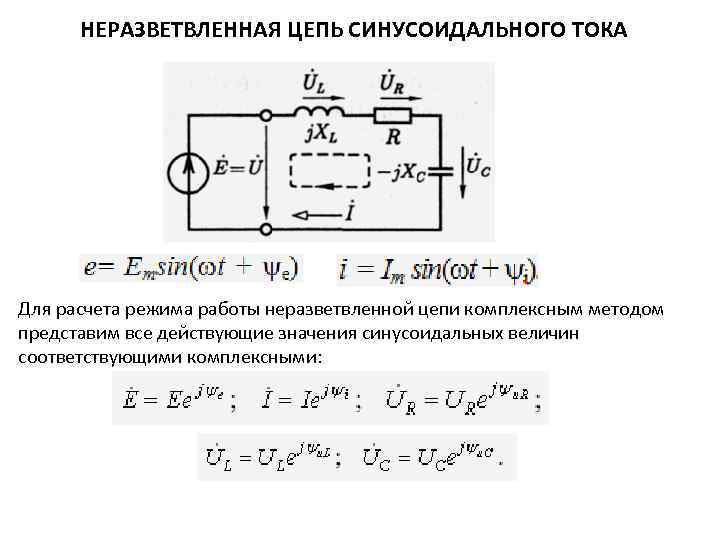
Методика расчета используется как в цепях постоянного, так и переменного напряжения. При расчетах цепей переменного напряжения с реактивными элементами используются комплексные величины, затем вычисляются мгновенные и амплитудные величины токов и напряжений и углы сдвига фаз между ними.
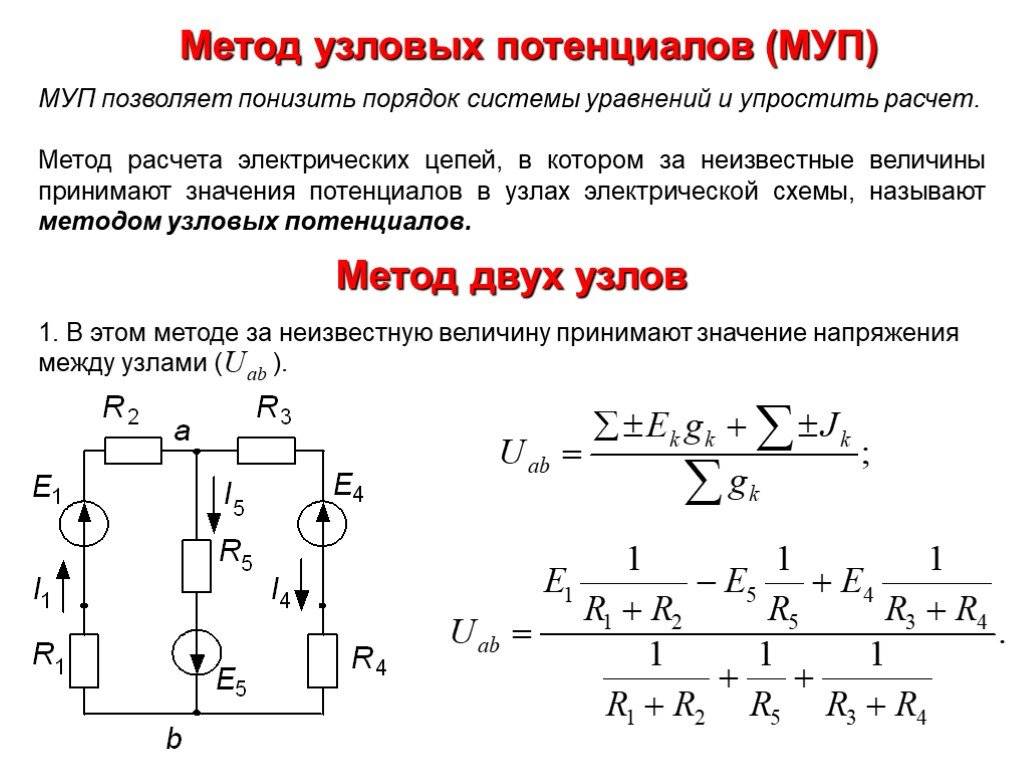
Метод узловых (потенциалов) напряжений
ТОЭ › Методы расчета цепей постоянного тока
При изучении основ электротехники приходится сталкиваться с необходимостью расчета тех или иных параметров различных схем. И самое простое, что приходится делать – это расчет токов ветвей в цепях постоянного тока.
Существует несколько наиболее применяемых методов расчетов для таких цепей: с помощью законов Кирхгофа, методом контурных токов, узловых потенциалов, методом эквивалентного генератора, эквивалентного источника тока, методом наложения. Для расчета более сложных цепей, например, в нелинейных схемах, могут применяться метод аппроксимации, графические методы и другие. В данном разделе рассмотрим один из методов определения токов в цепи постоянного тока – метод узловых потенциалов.
Важно отличать метод узловых напряжений (потенциалов) от метода узлового напряжения (метод двух узлов)
Метод узловых потенциалов примеры решения задач
Для того, чтобы лучше разобраться в этом вопросе, рассмотрим конкретный пример схемы, показанной на рис.1.
Рис.1. Схема постоянного тока
Для начала обозначают направления токов в ветвях. Направление можно выбирать любым. Если в результате вычислений какой-то из токов получится с отрицательным значением, значит, его направление в действительности будет направлено в противоположную сторону относительно ранее обозначенного. Если в ветви имеется источник, то для удобства лучше обозначить направление тока в этой ветви совпадающим с направлением источника в этой ветви, хотя и не обязательно. Далее один из узлов схемы заземляем. Заземленный узел будет называться опорным, или базисным. Такой метод заземления на общее токораспределение в схеме влияния не оказывает.
Какой именно узел заземлять, значения не имеет. Заземлим, например, узел 4 φ4 = 0.
Каждый из этих узлов будет обладать своим значением потенциала относительно узла 4. Именно значения этих потенциалов для дальнейшего определения токов и находят. Соответственно, для удобства этим потенциалам присваивают номера в соответствии с номером узла, т.е. φ1, φ2, φ3. Далее составляется система уравнений для оставшихся узлов 1, 2, 3.
В общем виде система имеет вид:
Использованные в этой системе уравнений буквенно-цифровые обозначения
имеют следующий смысл:
– сумма проводимостей ветвей, сходящихся в узле 1. В данном случае
– сумма проводимостей ветвей, сходящихся в узле 2. В данном случае
– сумма проводимостей ветвей, сходящихся в узле 3. В данном случае
– сумма проводимостей ветвей, соединяющих узлы 1 и 2, взятая со знаком «минус». Для этого единица и взята с отрицательным знаком:
– сумма проводимостей ветвей, соединяющих узлы 1 и 3, взятая со знаком «минус». Для этого единица и в этом случае взята с отрицательным знаком:
Аналогично находятся и остальные проводимости:
J11 – узловой ток узла 1, в котором участвуют ветви, подходящие именно к этому узлу, и содержащие в своем составе ЭДС. При этом, если ЭДС ветви, входящий в узел, направлена к рассматриваемому узлу (в данном случае к узлу 1), то такой узловой ток записывается с плюсом, если от узла, то с минусом. В данном случае
Аналогично
В результате всех ранее приведенных вычисленных значений исходная система уравнений примет вид:
Решать данную систему можно всеми доступными методами, мы же для упрощения решим ее в пакете Mathcad:
В результате получены следующие значения потенциалов в узлах цепи:
Токи в ветвях находятся в соответствии с законом Ома. Поясним это простыми словами.
В ветви с сопротивлением и источником, учитывая ранее обозначенное направление тока в рассматриваемой ветви, необходимо из потенциала узла, находящегося у начала стрелки направления тока, вычесть потенциал узла, находящегося у конца стрелки направления тока, а затем прибавить значение ЭДС в этой ветви. Далее все это разделить на сопротивление, имеющееся в ветви. Если бы ток и ЭДС в рассматриваемой ветви не совпадали по направлению, тогда значение ЭДС вычиталось. В ветви без ЭДС действует то же самое правило, только ЭДС в числителе, разумеется, отсутствует. В нашем примере получим, что
Значение тока первой ветви, как видно из расчета, получилось отрицательным. Значит, в действительности, этот ток направлен в противоположную сторону относительно его обозначенного направления на рис.1.
Правильность расчетов можно проверить, например, составлением баланса мощностей либо, к примеру, моделированием, схемы. Выполним моделирование в программе Multisim.
Рис.2. Моделирование в Multisim
Как видим, результаты моделирования совпадают с расчетными значениями. Незначительная разница в тысячных долях из-за округлений промежуточных вычислений.
Сила тока и закон Ома
Осуществляя расчет силы тока цепи, следует помнить, что эта величина физического типа, демонстрирующая определенный заряд. Он протекает за некоторую временную единицу по проводнику. Базовая схема вычисления следующая:
I=q/t, где:
- I – сила электричества в Амперах (А) или Кл/с;
- q – заряд, перемещающийся в рамках проводника в Кулонах (Кл);
- t – время, затраченное на перемещение заряда, с.
В соответствии с положениями закона Ома для отдельной части цепи при вычислении силы тока применяется схема, показывающая:
- прямую зависимость силы тока от напряжения;
- взаимосвязь обратного типа с сопротивлением.
I=U/R, где:
- U – выраженное в вольтах напряжение, В;
- R – показатель сопротивления, Ом.
Отсюда будет следовать такая зависимость:
I = E/ R+r, где:
- Е – ЭДС, В;
- R – сопротивление внешнего типа, Ом
- r – сопротивление внутреннее, Ом
Воспользуйтесь другими онлайн калькуляторами:
EveryCircuit
4. EveryCircuit представляет собой электронный эмулятор онлайн с хорошими сделанными графиками. Когда вы входите в онлайн программу, и она будет просить вас создать бесплатный счет, чтобы вы можете сохранить ваши проекты и иметь ограниченную часть площади рисовать вашу схему. Чтобы использовать его без ограничений, требующих годовой взнос в размере $ 10. Он можно скачивать и использоваться на платформах Android и iTunes. Компоненты имеют ограниченную способность имитировать с небольшими минимальными параметрами. Очень просто в использовании, он имеет прекрасную систему электронного дизайна. Она позволяет вам включать (вставлять) моделирование в ваши веб-страницы.