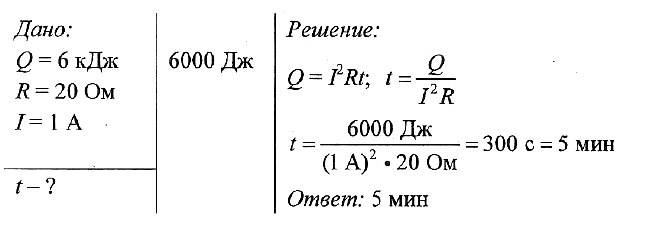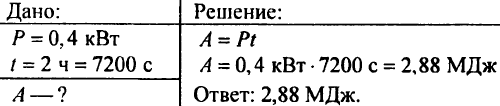Сколько времени работал обогреватель если при силе тока 4 а

От чего зависит реальная потребляемая мощность

Наиболее существенно потребляемая мощность электрокотла отопления зависит от:

1. Условий эксплуатации. А именно от желаемого температурного режима (снижение температуры на 1°C подразумевает до 5% экономии), постоянства проживания в доме и регулирования показателей на время сна или отсутствия хозяев дома.
2. Технического состояния котла. А именно его ТЭНов (трубчатых электронагревателей). При использовании в качестве теплоносителя жесткой, неочищенной и постоянно сменяемой воды на ТЭНах образуется накипь, что снижает КПД с 99% до 90,80 и даже 70%. Чтобы нагреть теплоноситель до прежней температуры через слой накипи, электрокотлу требуется больше энергозатрат и времени.
3. Оснащения. Циркуляционный насос и продвинутая автоматика потребляют от 60 до 150 Вт. Однако это не столь существенные значения на фоне и так дорогостоящих эксплуатационных расходов.
4. Функциональности автоматики. Продвинутая современная автоматика имеет несколько режимов работы, более грамотно управляет включением и выключением ТЭНов, работой циркуляционного насос, плавно регулирует температуру, позволяет задать значения гистерезиса. Электрокотлы средней и выше ценовой категории часто оснащены возможностью программирования режима работы, что существенно влияет на расход.

Задачи на нахождение силы тока в цепи, напряжения. Как решать задачи на закон Ома.

Задачи на силу тока в основном касаются определения силы тока, напряжения и сопротивления. В данном разделе Вы найдете формулы для решения задач. Мы разберем решение типичных элементарных задач, используя закон Ома.

Задача 1. Сила тока

Через нить накаливания лампочки от карманного фонарика за 2 мин проходит электрический заряд, равный 30 Кл. Определите силу тока в этой лампочке.

Дано:	CИ	Решение
q = 30 Кл	Сила тока I определяется по формуле
t = 2 мин	120 с	I= q/t
I – ?	I = 30Кл/120с = 0,25А = 250м А

Сила тока. Решение задач

Задача 2. Напряжение в цепи

Электродвигатель включен в электрическую цепь с напряжением 24В. Определите заряд, прошедший через электродвигатель, если при этом была совершена работа, равная 84 кДж

Дано:	CИ	Решение
U = 24 В	Напряжение на электродвигателе определяется по формуле
А = 84 кДж	84000 Дж	U=A/qq= A/U
q – ?	Q = 84000 Дж/24 В = 3500 Кл

Напряжение в цепи. Решение задач

Задача 3. Закон Ома сила тока

Определите силу тока в кипятильнике, включенном в сеть с напряжением 220 В, если сопротивление спирали составляет 55 Ом.

Дано:	CИ	Решение
U = 220 В	Силу тока в кипятильнике можно определить, воспользовавшись законом Ома
R = 55 Ом	І=U/R
І – ?	І = 220 B/55 Ом = 4 А

Сила тока по закону Ома. Решение задач

Задача 4. Закон Ома напряжение

Какое напряжение нужно приложить к концам проводника сопротивлением 5 Ом, тобі по проводнику пошел ток с силой тока, равной 300 мА

Дано:	CИ	Решение
R = 5 Ом	Необходимое напряжение можно определить, воспользовавшись законом Ома
І = 300 мА	0.3 A	І=U/RU = IR
U – ?	U = 0,3 А * 5 Ом = 1,5 В

Напряжение в сети. Закон Ома

Задача 5. Сопротивление по закону Ома

Определите cопротивление резистора, если за время 10 мин через него проходит заряд 200 Кл. Напряжение на концах резистора равно 6 В.

Источник

Рассчитываем сколько электроэнергии потребляет электрический котел в час, сутки и месяц

Практически все современные электрокотлы имеют КПД 99% и более. Это значит, что при максимальной нагрузке электрокотел мощностью 12 кВт будет потреблять 12,12 кВт электроэнергии. Электрокотел теплопроизводительностью 9 кВт – 9,091 кВт электроэнергии в час. Итого, максимально возможный расход котла мощностью 9 кВт:

1. В сутки – 24 (часа) * 9,091 (кВт) = 218,2 кВт. В стоимостном выражении при актуальном на первое полугодие 2020 года тарифе для Московской области – 218,2 (кВт) * 3,89 (руб. за 1 кВт.ч) = 848,8 руб/сутки.
2. В месяц электрокотел потребляет – 30 (дней) * 218,2 (кВт) = 6 546 кВт. В стоимостном выражении – 25 463,9 руб/мес.
3. За отопительный сезон (предположим, с 15 октября по 31 марта) – 136 (дней) * 218,2 (кВт) = 29 675,2 кВт. В стоимостном выражении – 115 436,5 руб/сезон.

Однако грамотно подобранный по мощности котлоагрегат никогда не работает при максимальной нагрузке 24/7. В среднем в течение отопительного сезона электрокотел потребляет около 40-70% от максимальной мощности, то есть работает лишь 9-16 часов в сутки. Так, на практике в среднестатистическом кирпичном доме 70-80 м2 в климатической зоне Подмосковья тот же котел мощностью 9 кВт требует расхода в 11-15 тыс. рублей в месяц.

Как рассчитать необходимую мощность котлаИндивидуальный расчет, формула и корректирующие коэффициенты

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Силу тока в проводнике увеличили в 2 раза. Как изменится количество теплоты, выделяющееся в нём за единицу времени, при неизменном сопротивлении проводника?

1) увеличится в 4 раза
2) уменьшится в 2 раза
3) увеличится в 2 раза
4) уменьшится в 4 раза

2. Длину спирали электроплитки уменьшили в 2 раза. Как изменится количество теплоты, выделяющееся в спирали за единицу времени, при неизменном напряжении сети?

1) увеличится в 4 раза
2) уменьшится в 2 раза
3) увеличится в 2 раза
4) уменьшится в 4 раза

3. Сопротивления резистор ​\( R_1 \)​ в четыре раза меньше сопротивления резистора ​\( R_2 \)​. Работа тока в резисторе 2

1) в 4 раза больше, чем в резисторе 1
2) в 16 раз больше, чем в резисторе 1
3) в 4 раза меньше, чем в резисторе 1
4) в 16 раз меньше, чем в резисторе 1

4. Сопротивление резистора ​\( R_1 \)​ в 3 раза больше сопротивления резистора ​\( R_2 \)​. Количество теплоты, которое выделится в резисторе 1

1) в 3 раза больше, чем в резисторе 2
2) в 9 раз больше, чем в резисторе 2
3) в 3 раза меньше, чем в резисторе 2
4) в 9 раз меньше, чем в резисторе 2

5. Цепь собрана из источника тока, лампочки и тонкой железной проволоки, соединенных последовательно. Лампочка станет гореть ярче, если

1) проволоку заменить на более тонкую железную
2) уменьшить длину проволоки
3) поменять местами проволоку и лампочку
4) железную проволоку заменить на нихромовую

6. На рисунке приведена столбчатая диаграмма. На ней представлены значения напряжения на концах двух проводников (1) и (2) одинакового сопротивления. Сравните значения работы тока ​\( A_1 \)​ и ​\( A_2 \)​ в этих проводниках за одно и то же время.

1) ​\( A_1=A_2 \)​
2) \( A_1=3A_2 \)
3) \( 9A_1=A_2 \)
4) \( 3A_1=A_2 \)

7. На рисунке приведена столбчатая диаграмма. На ней представлены значения силы тока в двух проводниках (1) и (2) одинакового сопротивления. Сравните значения работы тока \( A_1 \)​ и ​\( A_2 \) в этих проводниках за одно и то же время.

1) ​\( A_1=A_2 \)​
2) \( A_1=3A_2 \)
3) \( 9A_1=A_2 \)
4) \( 3A_1=A_2 \)

8. Если в люстре для освещения помещения использовать лампы мощностью 60 и 100 Вт, то

А. Большая сила тока будет в лампе мощностью 100 Вт.
Б. Большее сопротивление имеет лампа мощностью 60 Вт.

Верным(-и) является(-ются) утверждение(-я)

1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б

9. Электрическая плитка, подключённая к источнику постоянного тока, за 120 с потребляет 108 кДж энергии. Чему равна сила тока в спирали плитки, если её сопротивление 25 Ом?

1) 36 А
2) 6 А
3) 2,16 А
4) 1,5 А

10. Электрическая плитка при силе тока 5 А потребляет 1000 кДж энергии. Чему равно время прохождения тока по спирали плитки, если её сопротивление 20 Ом?

1) 10000 с
2) 2000 с
3) 10 с
4) 2 с

11. Никелиновую спираль электроплитки заменили на нихромовую такой же длины и площади поперечного сечения. Установите соответствие между физическими величинами и их возможными изменениями при включении плитки в электрическую сеть. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) электрическое сопротивление спирали
Б) сила электрического тока в спирали
B) мощность электрического тока, потребляемая плиткой

ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличилась
2) уменьшилась
3) не изменилась

12. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются. Запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) работа тока
Б) сила тока
B) мощность тока

ФОРМУЛЫ
1) ​\( \frac{q}{t} \)​
2) ​\( qU \)​
3) \( \frac{RS}{L} \)​
4) ​\( UI \)​
5) \( \frac{U}{I} \)​

Часть 2

13. Нагреватель включён последовательно с реостатом сопротивлением 7,5 Ом в сеть с напряжением 220 В. Каково сопротивление нагревателя, если мощность электрического тока в реостате составляет 480 Вт?

Решение задач по теме Электрический ток

ЗАДАЧА 1.

Через нить накаливания лампочки от карманного фонарика за 2 мин проходит электрический заряд, равный 30 Кл. Определите силу тока в этой лампочке.

Запишем условие задачи и решим её.

Ответ: I = 250 мА.

ЗАДАЧА 2.

Электродвигатель включён в электрическую цепь с напряжением 24 В. Определите заряд, прошедший через электродвигатель, если при этом была совершена работа, равная 84 кДж.

Ответ: q = 3500 Кл.

ЗАДАЧА 3.

Определите силу тока в кипятильнике, включённом в сеть с напряжением 220 В, если сопротивление спирали составляет 55 Ом.

Ответ: I = 4 А.

ЗАДАЧА 4.

Какое напряжение нужно приложить к концам проводника сопротивлением 5 Ом, чтобы по проводнику пошёл ток с силой тока, равной 300 мА?

Ответ: U = 1,5 В.

ЗАДАЧА 5.

Определите сопротивление резистора, если за время 10 мин через него проходит заряд 200 Кл. Напряжение на концах резистора равно 6 В.

Ответ: R = 18 Ом.

ИТОГИ темы «Электрический ток»

• Электрическим током называют упорядоченное движение заряженных частиц под действием электрического поля.
• Сила тока — это физическая величина, которая показывает, какой электрический заряд проходит через поперечное сечение проводника за единицу времени.
• Работу электрического поля, создающего электрический ток, называют работой тока.
• Напряжение показывает, какую работу совершает электрическое поле при перемещении единичного электрического заряда из одной точки поля в другую.
• Электрическое сопротивление характеризует свойство проводника препятствовать протеканию в нём электрического тока.
• Закон Ома гласит: сила тока на участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна сопротивлению.

Вы смотрели Конспект по физике для 8 класса «Решение задач. Электрический ток».

Источник

Электродвигатель включен в электрическую цепь с напряжением 24 в

При напряжении 120 В электрическая лампа в течение 0,5 мин потребила 900 Дж энергии. Чему равна сила тока в лампе? Ответ запишите в амперах.

Мощность есть отношение работы ко времени в течение которого работа совершалась. В данном случае работа равна потреблённой энергии тогда

С другой стороны, мощность электрического тока равна произведению напряжения на силу тока, откуда

При напряжении 120 В электрическая лампа в течение 0,5 мин потребила 900 Дж энергии. Сила тока в лампе равна

Мощность есть отношение работы ко времени в течение которого работа совершалась. В данном случае работа равна потреблённой энергии тогда

С другой стороны, мощность электрического тока равна произведению напряжения на силу тока, откуда

Правильный ответ указан под номером 2.

На велосипеде установлен генератор, вырабатывающий электрическую энергию для двух последовательно соединённых ламп. В каждой лампе сила тока 0,3 А при напряжении на каждой лампе 6 В. Чему равна работа тока генератора за 2 часа? Ответ запишите в килоджоулях.

Электрическая мощность равна произведению напряжения на силу тока. Работа равна произведению мощности на промежуток времени. Таким образом, на одной лампе совершается работа тока: 0,3 А · 6 В · 7200 с = 12960 Дж.

Следовательно, работа тока генератора на двух лампах равна 2 · 12960 Дж = 25,92 кДж.

Электродвигатель постоянного тока работает при напряжении 220 В и силе тока 40 А. Полезная мощность двигателя 6,5 кВт. Чему равен КПД электродвигателя?

Коэффициент полезного действия определяется как отношение полезной мощности к затрачиваемой мощности. Найдём затрачиваемую мощность:

Правильный ответ указан под номером 2.

На велосипеде установлен генератор, вырабатывающий электрическую энергию для двух последовательно соединённых ламп. В каждой лампе сила тока 0,3 А при напряжении на каждой лампе 6 В. Чему равна работа тока генератора за 2 часа?

Электрическая мощность равна произведению напряжения на силу тока. Работа равна произведению мощности на промежуток времени. Таким образом, на одной лампе совершается работа тока: 0,3 А · 6 В · 7200 с = 12960 Дж.

Следовательно, работа тока генератора на двух лампах равна 2 · 12960 Дж = 25,92 кДж.

Правильный ответ указан под номером 3.

Две лампы, рассчитанные на одинаковое напряжение, но потребляющие различную мощность, включены в электрическую сеть последовательно. Какая лампа будет горeть ярче? Ответ поясните.

Мощность лампы рассчитывается по формуле

Имеется два электрических нагревателя одинаковой мощности — по 400 Вт. Сколько времени потребуется для нагревания 1 л воды на 40 °С, если нагреватели будут включены в электросеть последовательно? Потерями энергии пренебречь.

Для нагревания массы воды m = ρV потребуется количество теплоты

Эта энергия выделится на нагревателях за время τ:

где W — общая мощность последовательно соединённых нагревателей.

Запишем уравнение теплового баланса: Q = E, и выразим искомое время:

Нагреватель представляет собой резистор, на котором при прохождении тока выделяется тепло. Как и у любого другого электрического сопротивления, мощность тепловыделения зависит от величины протекающего тока по закону Джоуля — Ленца

U

Подставляя числовые значения в формулу для времени, получаем:

Источник

Применение и практический смысл

Непосредственное превращение электричества в тепловую энергию нельзя назвать экономически выгодным. Однако, с точки зрения удобства и доступности современного человечества к источникам электроэнергии различные нагревательные приборы продолжают массово применяться как в быту, так и на производстве.

Перечислим некоторые из них:

• электрочайники;
• утюги;
• фены;
• варочные плиты;
• паяльники;
• сварочные аппараты и многое другое.

На рисунке 3 изображены бытовые нагревательные приборы, которыми мы часто пользуемся.

Рис. 3. Бытовые нагревательные приборы

Использование тепловых мощностей в химической, металлургической и в других промышленных отраслях тесно связно с использованием электрической энергии.

Без знания физического закона Джоуля-Ленца было бы невозможно сконструировать безопасный нагревательный прибор. Для этого нужны расчёты, которые невозможно сделать без применения рассмотренных нами формул. На основе расчётов происходит выбор материалов с нужным удельным сопротивлением, влияющим на нагревательную способность устройств.

Закон Джоуля-Ленца без преувеличения можно назвать гениальным. Это один из тех законов, которые повлияли на развитие электротехники.

Почему греется проводник

Как же объясняется нагрев проводника? Почему он именно греется, а не остаётся нейтральным или охлаждается? Нагрев происходит из-за того, что свободные электроны, перемещающиеся в проводнике под действием электрического поля, бомбардируют атомы молекул металла, тем самым передавая им собственную энергию, которая переходит в тепловую. Если изъясняться совсем просто: преодолевая материал проводника, электрический ток как бы “трётся”, соударяется электронами о молекулы проводника. Ну а , как известно, любое трение сопровождается нагревом. Следовательно, проводник будет нагреваться пока по нему бежит электрический ток.

Из формулы также следует –  чем выше удельное сопротивление проводника и чем выше сила тока протекающего по нему, тем выше будет нагрев . Например, если последовательно соединить проводник-медь (удельное сопротивление  0,018 Ом·мм²/м) и проводник-алюминий (0,027 Ом·мм²/м), то при протекании через цепь электрического тока алюминий будет нагреваться сильнее чем медь из-за более высокого сопротивления. Поэтому, кстати, не рекомендуется в быту делать скрутки медных и алюминиевых проводов друг с другом – будет неравномерный нагрев в месте скрутки. В итоге –  подгорание с последующим пропаданием контакта.

Опыты Ленца

Перенесемся в 19 век-эпоху накопления знаний и подготовки к технологическому прыжку 20 века. Эпоха, когда по всему миру различные учёные и просто изобретатели-самоучки чуть ли не ежедневно открывают что-то новое, зачастую тратя огромное количество времени на исследования и, при этом, не представляя конечный результат.

Один из таких людей, русский учёный Эмилий Христианович Ленц, увлекался электричеством, на тогдашнем примитивном уровне, пытаясь рассчитывать  электрические цепи. В 1832 году  Эмилий Ленц “застрял” с расчётами, так как параметры его смоделированной цепи “источник энергии – проводник – потребитель энергии” сильно разнились от опыта к опыту. Зимой 1832-1833 года учёный обнаружил, что причиной нестабильности является кусочек платиновой проволоки, принесённый им с холода. Отогревая или охлаждая проводник, Ленц также заметил что  существует некая  зависимость между силой тока, электрическим сопротивлением  и температурой проводника.

При определённых параметрах электрической цепи проводник быстро оттаивал и даже слегка нагревался. Измерительных приборов в те времена практически никаких не существовало – невозможно было точно измерить ни силу тока, ни сопротивление. Но это был русский физик, и он проявил смекалку. Если это зависимость, то почему бы ей не быть обратимой?

Для того чтобы измерить количество тепла, выделяемого проводником, учёный сконструировал простейший “нагреватель” – стеклянная ёмкость, в которой находился  спиртосодержащий раствор и погружённый в него платиновый проводник-спираль. Подавая различные величины электрического тока на проволоку, Ленц замерял время, за которое раствор нагревался до определённой температуры. Источники электрического тока в те времена  были слишком слабы, чтобы разогреть раствор до серьёзной температуры, потому визуально определить количество испарившегося  раствора не представлялось возможным. Из-за этого процесс исследования очень затянулся – тысячи вариантов подбора параметров источника питания, проводника, долгие замеры и последующий анализ.

Опыты Ленца

Перенесемся в 19 век-эпоху накопления знаний и подготовки к технологическому прыжку 20 века. Эпоха, когда по всему миру различные учёные и просто изобретатели-самоучки чуть ли не ежедневно открывают что-то новое, зачастую тратя огромное количество времени на исследования и, при этом, не представляя конечный результат.

Один из таких людей, русский учёный Эмилий Христианович Ленц, увлекался электричеством, на тогдашнем примитивном уровне, пытаясь рассчитывать  электрические цепи. В 1832 году  Эмилий Ленц «застрял» с расчётами, так как параметры его смоделированной цепи «источник энергии — проводник — потребитель энергии» сильно разнились от опыта к опыту. Зимой 1832-1833 года учёный обнаружил, что причиной нестабильности является кусочек платиновой проволоки, принесённый им с холода. Отогревая или охлаждая проводник, Ленц также заметил что  существует некая  зависимость между силой тока, электрическим сопротивлением  и температурой проводника.

При определённых параметрах электрической цепи проводник быстро оттаивал и даже слегка нагревался. Измерительных приборов в те времена практически никаких не существовало — невозможно было точно измерить ни силу тока, ни сопротивление. Но это был русский физик, и он проявил смекалку. Если это зависимость, то почему бы ей не быть обратимой?

Для того чтобы измерить количество тепла, выделяемого проводником, учёный сконструировал простейший «нагреватель» — стеклянная ёмкость, в которой находился  спиртосодержащий раствор и погружённый в него платиновый проводник-спираль. Подавая различные величины электрического тока на проволоку, Ленц замерял время, за которое раствор нагревался до определённой температуры. Источники электрического тока в те времена  были слишком слабы, чтобы разогреть раствор до серьёзной температуры, потому визуально определить количество испарившегося  раствора не представлялось возможным. Из-за этого процесс исследования очень затянулся — тысячи вариантов подбора параметров источника питания, проводника, долгие замеры и последующий анализ.

Где может пригодиться этот закон Джоуля-Ленца?

В электротехнике есть понятие длительно допустимого тока протекающего по проводам. Это такой ток, который провод способен выдержать длительное время (то есть, бесконечно долго), без разрушения провода (и изоляции, если она есть, потому что провод может быть и без изоляции). Конечно, данные вы теперь можете взять из ПУЭ (Правила устройства электроустановок), но получали эти данные исключительно на основе закона Джоуля-Ленца.

В электротехнике так же используются плавкие предохранители. Их основное качество – надёжность срабатывания. Для этого используется проводник определенного сечения. Зная температуру плавления такого проводника можно вычислить количество теплоты, которое необходимо, чтобы проводник расплавился от протекания через него больших значений тока, а вычислив ток, можно вычислить и сопротивление, которым такой проводник должен обладать. В общем, как вы уже поняли, применяя закон Джоуля-Ленца можно рассчитать сечение или сопротивление (величины взаимозависимы) проводника для плавкого предохранителя.

А ещё, помните, мы говорили про . Там на примере лампочки я рассказывал парадокс, что более мощная лампа в последовательном соединении светит слабее. И наверняка помните почему: падение напряжения на сопротивлении тем сильнее, чем меньше сопротивление. А поскольку мощность — это , а напряжение очень сильно падает, то и выходит, что большое сопротивление выделит большое количество тепла, то есть, току придется больше потрудиться, чтобы преодолеть большое сопротивление. И количество тепла, которое выделит ток при этом можно посчитать с помощью закона Джоуля-Ленца. Если брать последовательное соединение сопротивлений, то использовать лучше выражение через квадрат тока, то есть, изначальный вид формулы:

А для параллельного соединения сопротивлений, поскольку ток в параллельных ветвях зависит от сопротивления, в то время, как напряжение на каждой параллельной ветви одинаковое, то формулу лучше всего представить через напряжение:

Примерами работы закона Джоуля-Ленца вы все пользуетесь в повседневной жизни – в первую очередь это всевозможные нагревательные приборы. Как правило, в них используется нихромовая проволока и толщина (поперечное сечение) и длина проводника подбираются с учётом того, чтобы длительное тепловое воздействие не приводило к стремительному разрушению проволоки. Точно таким же образом добиваются свечения вольфрамовой нити в лампе накаливания. По этому же закону определяют степень возможного нагрева практически любого электротехнического и электронного устройства.

В общем, несмотря на кажущуюся простоту, закон Джоуля-Ленца играет в нашей жизни очень огромную роль. Этот закон дал большой толчок для теоретических расчётов: выделение тепла токами , вычисление конкретной температуры дуги, проводника и любого другого электропроводного материала, потери электрической мощности в тепловом эквиваленте и т.д.

Вы можете спросить, а как перевести Джоули в Ватты и это довольно частый вопрос в интернете. Хотя вопрос несколько неверный, читая далее, вы поймёте почему. Ответ довольно прост: 1 дж = 0.000278 Ватт*час, в то время, как 1 Ватт*час = 3600 Джоулей. Напомню, что в Ваттах измеряется потребляемая мгновенная мощность, то есть непосредственно используемая пока включена цепь. А Джоуль определяет работу электрического тока, то есть мощность тока за промежуток времени. Помните, в законе Ома я приводил аллегорическую ситуацию. Ток – деньги, напряжение – магазин, сопротивление – чувство меры и денег, мощность – количество продуктов, которые вы сможете на себе унести (увезти) за один раз, а вот как далеко, как быстро и сколько раз вы сможете их увезти – это работа. То есть, сравнить работу и мощность никак не получается, но можно выразить в более понятных нам единицам: Ваттах и часах.

Думаю, что теперь вам не составит труда применить закон Джоуля-Ленца в практике и теории, если таковое потребуется и даже сделать перевод Джоулей в Ватты и наоборот. А благодаря пониманию, что закон Джоуля-Ленца это произведение электрической мощности на время, вы сможете более легко его запомнить и даже, если вдруг забыли основную формулу, то помня всего лишь закон Ома можно снова получить закон Джоуля-Ленца. А я на этом с вами прощаюсь.

Знаменитый русский физик Ленц и английский физик Джоуль, проводя опыты по изучению тепловых действий электрического тока, независимо друг от друга вывели закон Джоуля-Ленца. Данный закон отражает взаимосвязь количества теплоты, выделяемого в проводнике, и электрического тока, проходящего по этому проводнику в течение определенного периода времени.

Два лучших способа снизить потребление электрокотла

Как выбрать внешний термостат для электрокотла и экономить на отоплении до 30% каждый месяц

Программируемый комнатный термостат управляет работой котла ориентируясь на измерения температуры воздуха в помещении, в котором установлен, а не на температуру теплоносителя

Однако главной и наиболее важной в целях экономии задачей является режим программирования настроек работы на ближайшие сутки и неделю. Например, на рабочее время, когда хозяева отсутствуют дома, можно установить температуру 15°C

А на время сна – 18 или 19°C. Такие параметры не повлияют на комфорт, однако позволят существенно уменьшить итоговый расход электроэнергии.

Вторым незаменимым элементом при отоплении электрокотлом явяется электрический счетчик, дифферинцирующий потребление электроэнергии по двум, а лучше по трем временным зонам. Например, для Московской области действуют такие дифферинцированные по временным зонам тарифы:

• пиковая зона (с 7:00 до 10:00 и с 17:00 до 21:00) – 5.06 руб за 1 кВт.ч;
• полупиковая зона (с 10:00 до 17:00 и с 21:00 до 23:00)– 3.89 руб за 1 кВт.ч;
• ночная зона (с 23:00 до 7:00) – 1.68 руб за 1 кВт.ч.

На практике затраты на покупку, оформление и установку прибора учета, дифферинцирующего потребление, окупаются за несколько месяцев, поскольку снижают расходы в денежном выражении на 15-25%.

Вывод законов Ома и Джоуля-Ленца из классических электрон­ных представлений

Какова природа носителей тока в металлах? В 1901 г. Рикке проделал опыты: через 3 цилиндра, установленных друг на друга в течение 3-х лет пропускал постоянный ток. Был пропущен заряд, равный 3,5·10 6 Кл. Взвешивание показало неизменный вес цилинд­ров. Исследование торцов цилиндров не показало следов переноса вещества. Из этого был сделан вывод, что носители заряда не ионы, а открытые Томпсоном в 1897 г. электроны.

Чтобы отождествить носители заряда с электронами, нужно было определить знак и величину удельного заряда носителей.

Если в металле имеются легко перемещающиеся заряженные частицы, то при торможении металлического проводника эти час­тицы должны некоторое время продолжать двигаться по инерции, в результате чего в проводнике возникнет импульс тока и будет пе­ренесен некоторый заряд.

Мандельштам и Папалекси в 1913 г. проделали такой опыт – они приводили в быстрое крутильное колебание катушку с прово­дом вокруг ее оси. К концам катушки подключили телефон, в кото­ром был слышен звук, обусловленный импульсами тока. Был полу­чен качественный результат – зарегистрирован импульс тока.

Толмен и Стюарт в 1916 г. получили количественный ре­зультат. Катушка с проводом длиной 500 м приводилась во враще­ние со скоростью v=300 м/с. Катушка резко тормозилась и с по­мощью баллистического гальванометра измеряли заряд, протекав­ший в цепи во время торможения. Вычисленное значение отношения заряда к массе e/m полу­чалось очень близким для электронов. Таким образом было доказано, что носителем тока являются электроны. Исходя из представлений о свободных электронах была создана классическая теория электро­проводности металлов в предположении, что:

— электроны в металле ведут себя подобно молекулам иде­ального газа;

— движение электронов подчиняется законам классической механики;

— взаимодействие электронов сводится к соударениям с ио­нами кристалли-ческой решетки;

— силами взаимодействия между электронами можно пре­небречь и они между собой не сталкиваются;

— электроны в отсутствие электрического поля движутся хаотически.

Вычислим плотность тока j в проводнике, возникающего под действием поля напряженностью Е.

По определению плотность тока j = n e — это заряд, переносимый через единицу площади S = 1м 2 за единицу времени t=1 с; n – концентрация электронов, е – заряд элек­трона, — средняя скорость упорядоченного движения электро­нов.

На каждый электрон действует сила F = eE = ma, поэтому электрон приобретает ускорение и к концу свободного про­бега он достигнет скорости, а средняя скорость =v_max/2.

Если — средняя скорость теплового хаотичного движе­ния электронов, а средняя длина свободного пробега электронов , то среднее время между соударениями = . Подставляя в формулу для получим:

.

Подставляя в формулу для j, получим

,

т.е. плотность тока прямо пропорциональна Е, а это и есть выраже­ние закона Ома в дифференциальной форме. Если положить, что

то j = γ E.

Удельная проводимость γ

T, поэтому проводимость снижа­ется с ростом температуры, а удельное сопротивление по­вышается с ростом температуры. К концу свободного пробега электрон приоб­ретает кинетическую энергию

Предполагается, что вся энергия при соударении передается узлу кристаллической решетки и переходит в тепло. За 1 с электрон ис­пытывает / cоударений, а значит выделяет во столько же раз больше тепла. Если в единице объема n электронов, то в еди­нице объема за единицу времени выделится количество тепла

.

Таким образом, — выражение закона Джоуля-Ленца в дифференциальной форме.

При протекании по проводнику электрический ток оказывает на него тепловое действие, во время которого выделяется определенное значение количества теплоты. Для его расчета применяется закон Джоуля-Ленца, который получил широкое применение при проектировании и изготовлении всех устройств, работающих от электричества.