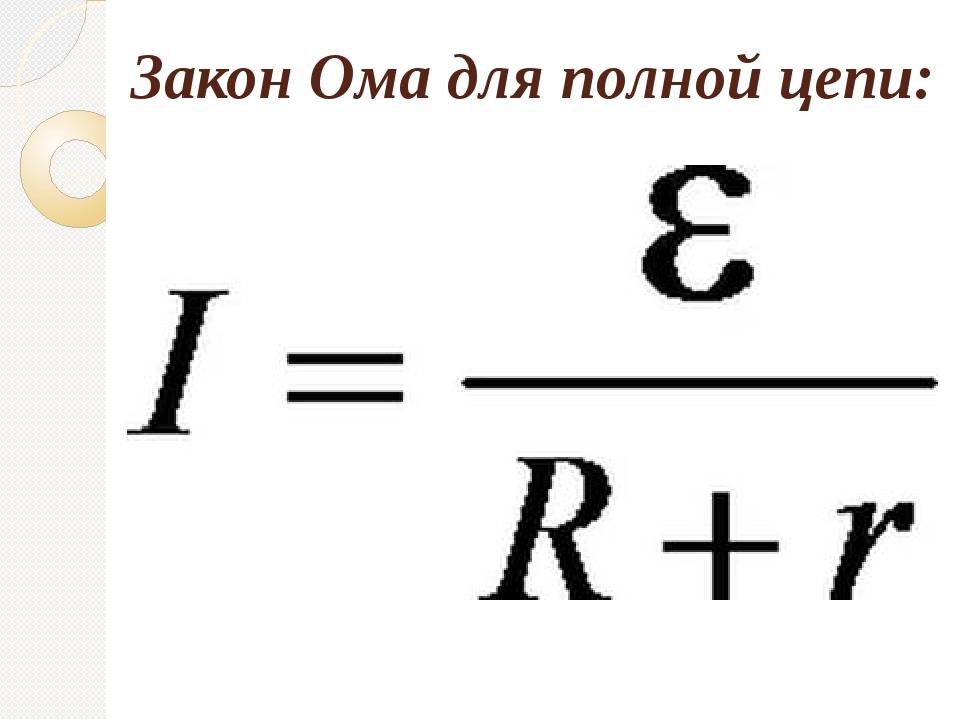Путь Георга Ома к открытию закона для полной цепи
Странно, но имя Георга Ома сегодня известно более, нежели Майкла Фарадея, подарившего человечеству первый электродвигатель (если говорить точнее, истинный изобретатель пожелал остаться неизвестным, направив письмо, опубликованное позже в научном журнале). Без простого закона не возникли бы отрасли науки, техника выродилась в труд лопатой. Нет радио, телевидения и персональных компьютеров.
Изначально Георг Ом работал учеником слесаря, но отец хотел дать детям образование. Деньги на книги отряжались безотносительно к материальному благополучию. Георг Ом быстро усваивал науку, становясь талантливым математиком. Муж науки проявился как талантливый спортсмен и отменный плясун, не имевший равных на студенческих вечеринках.
Не успев закончить образование, отец закона для полной цепи пошёл учителем младших классов. Работал одновременно воспитателем. Быть учителем в швейцарском городе Готтштадте Георгу Ому нравилось: живописная природа и неплохой заработок, но истинный триумф ждал первооткрывателя закона для полной цепи сквозь невзгоды в будущем. В 1809 году проза жизни снова на пороге: к местному священнику возвращается сын – математик по образованию. Георгу предлагают оставить должность преподавателя.

Георг Ом
Более десяти лет Ом перебивается от одного места работы к другому, не находя удовлетворительного места для преподавания. Пока волею судьбы не оказывается приглашённым в иезуитскую школу Кельна. Преподавательская нагрузка невелика, зато в заведении присутствует обширное хранилище приборов, по большей части устаревших или сломанных. Любопытно, что Георг Ом не спешит бежать с прошением о материальной помощи к ректорам. Вместо этого, припомнив старые навыки слесаря, берётся мастерить собственными руками. С интересом в письмах отцу рассказывает о новых конструкциях, обычных и гидростатических, доводит до совершенства отцовский способ шлифовки янтаря для создания электрических источников.
Одновременно Георг Ом уделяет много времени конструированию прибора, называемого электрометром (измерение заряда на основании опытов Шарля Кулона). На сцене уже прогремели слухи о гальванометрах Швейггера, и Ом понимает, что в стройности науки далеко до совершенства. В 1821 году пишет отцу, что предчувствует некое открытие и внимательно следит за событиями в этой отрасли.
Изначально Ом брал вольтов элемент из меди и цинка, заправленный соляной кислотой, а крутильными весами измерял усилие, необходимое, чтобы привести стрелку к магнитному меридиану Земли, пока на компас действовал проводник с током. Провод Георг Ом ориентировал по меридиану, исключая погрешность. Вольтов столб разряжался сравнительно быстро, угол отклонения стрелки постепенно менялся. Ом видел, что источник в обычном качестве для экспериментальной установки не годится.
Образцы проволоки первоначально опускались в чашу с ртутью (имеющей сравнительно низкую проводимость) и тщательно зачищались учёным для лучшего контакта. Жидкая среда препятствовала окислению материала и одновременно ограничивала рост тока до разумных пределов. 5 образцов медной проволоки разной длины поочерёдно участвовали в эксперименте. Обозначив образцы латинскими буквами a, b, c, d, e новоиспечённый учёный Георг Ом находит свой первый закон в логарифмической форме:

Первый закон Ома
Где за х принимает длину проволоки в футах, U характеризует магнитное поле. Результаты не удовлетворяют учёного и через время он вносит в зависимость две константы:
U = m ln (1 + x/a) – первоначальная формулировка закона Ома для полной цепи.
Закон Ома для цепи
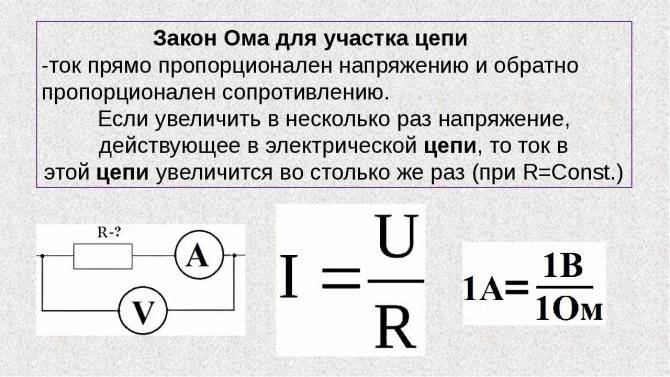
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Закон Ома для участка цепи.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
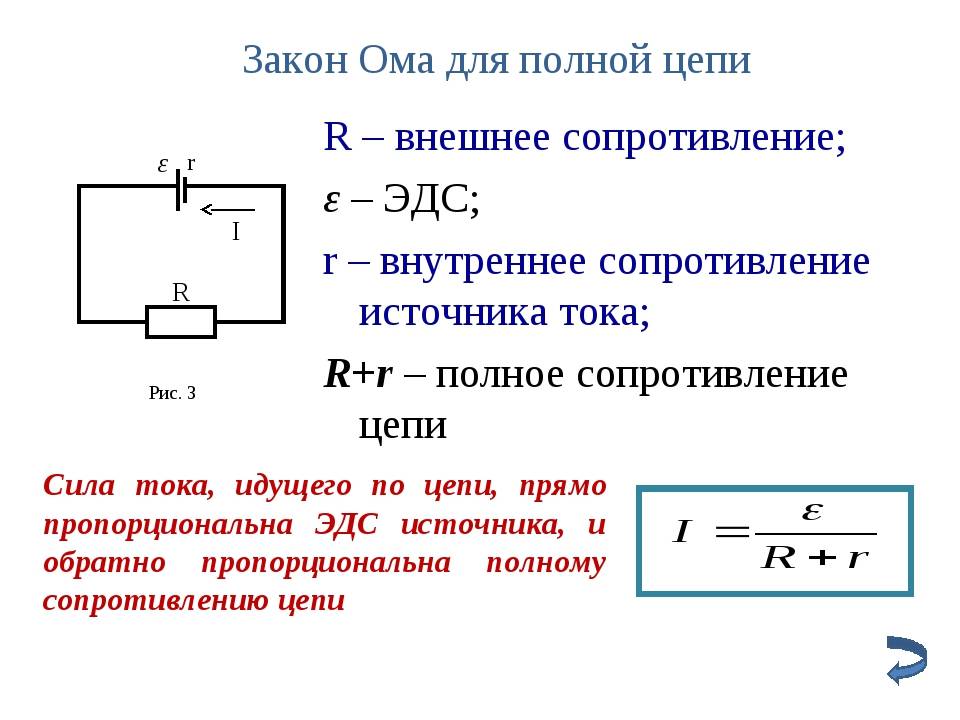
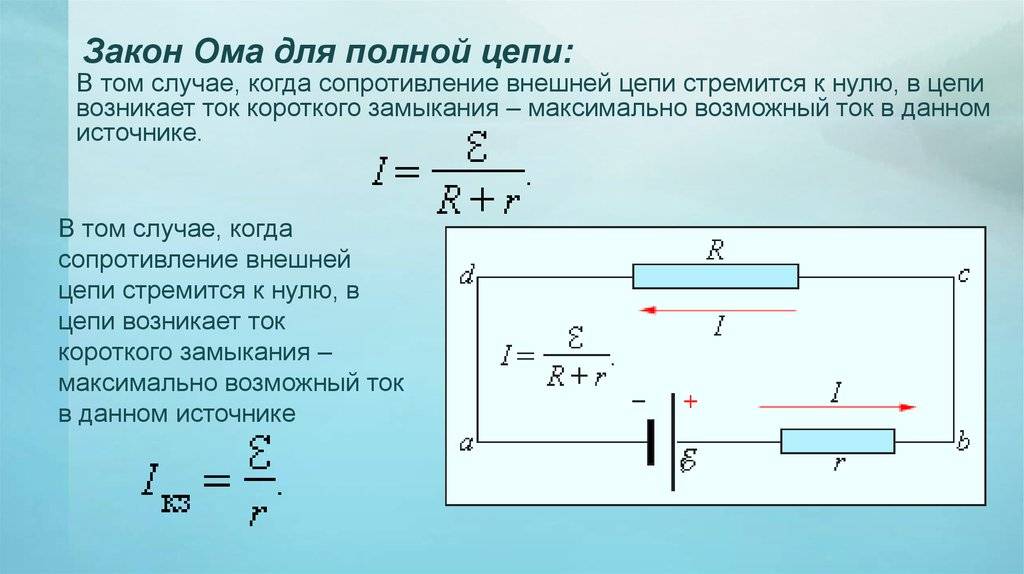
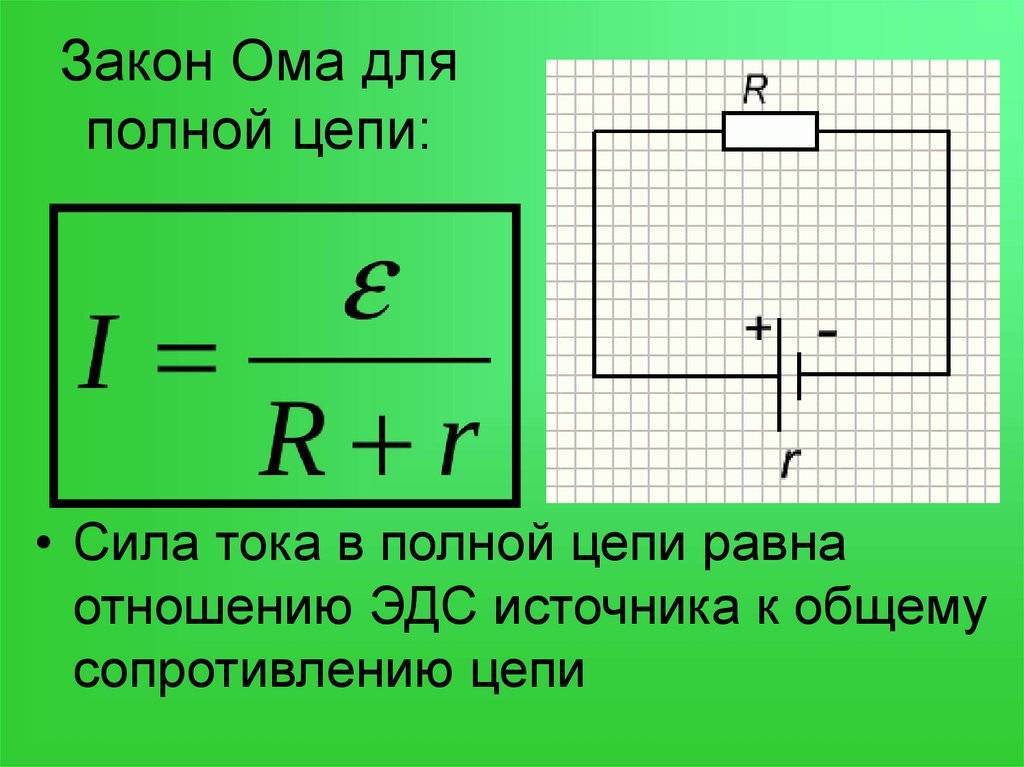
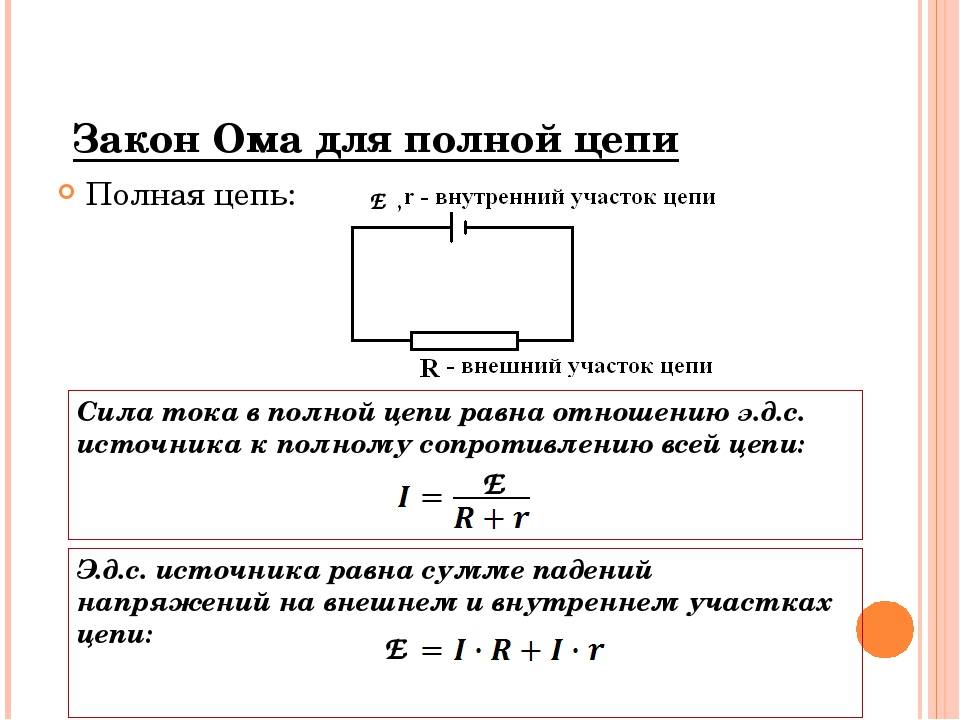
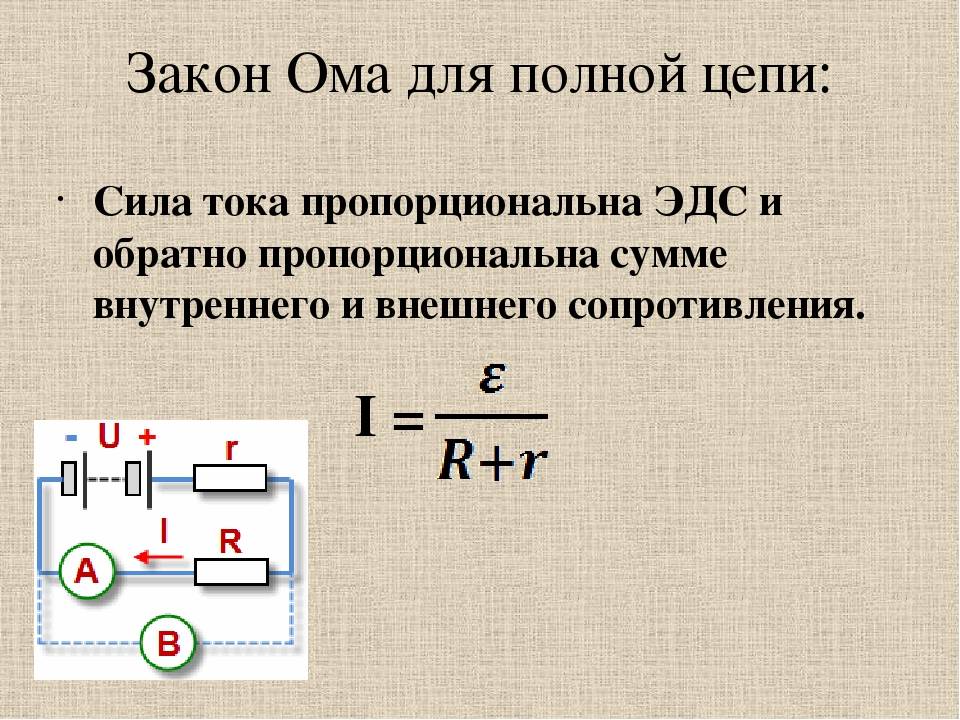
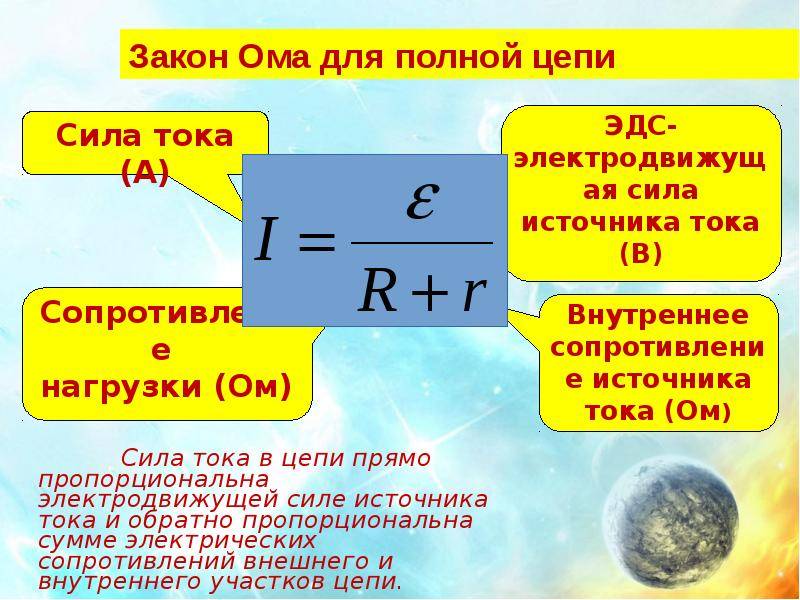
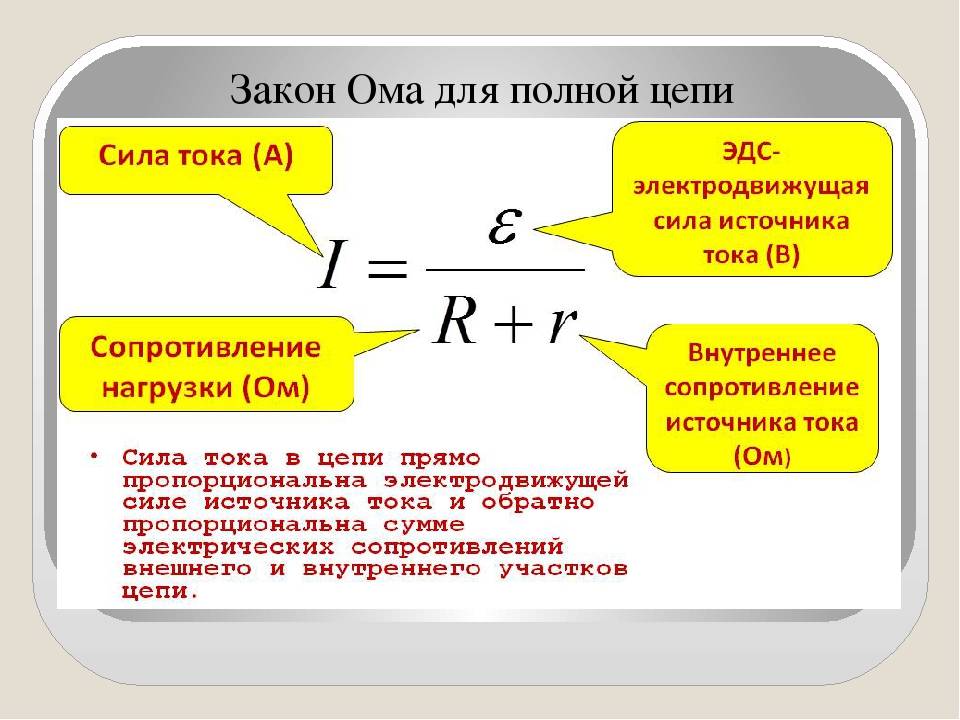
Для полной цепи
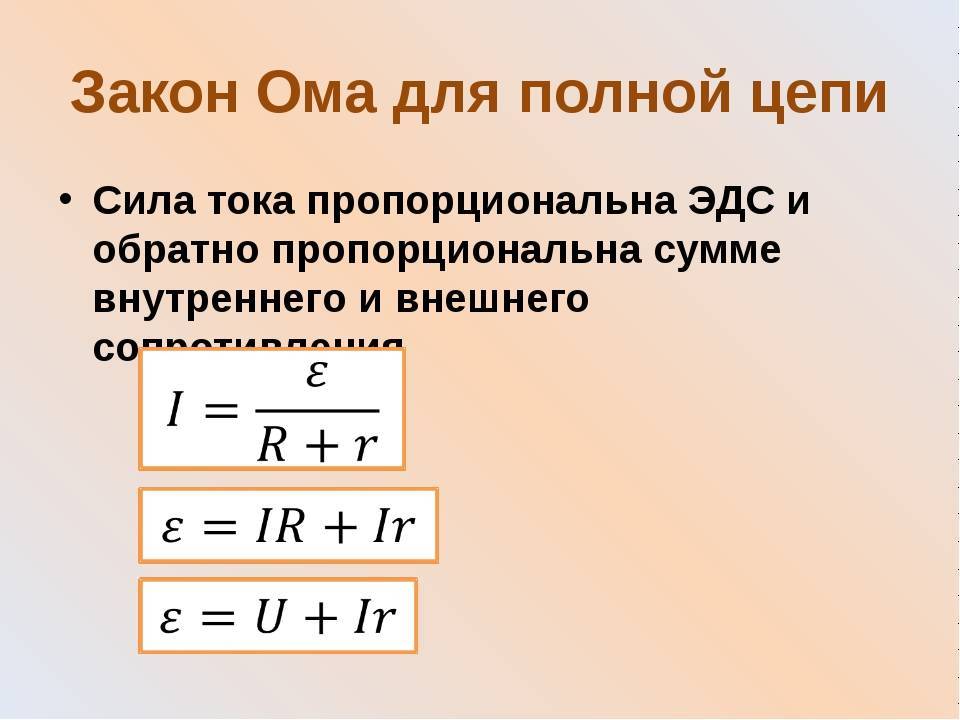
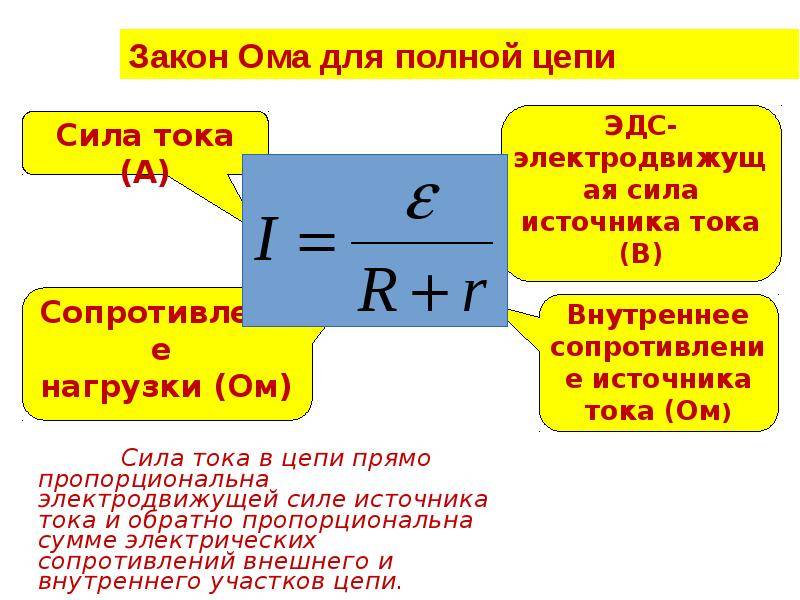
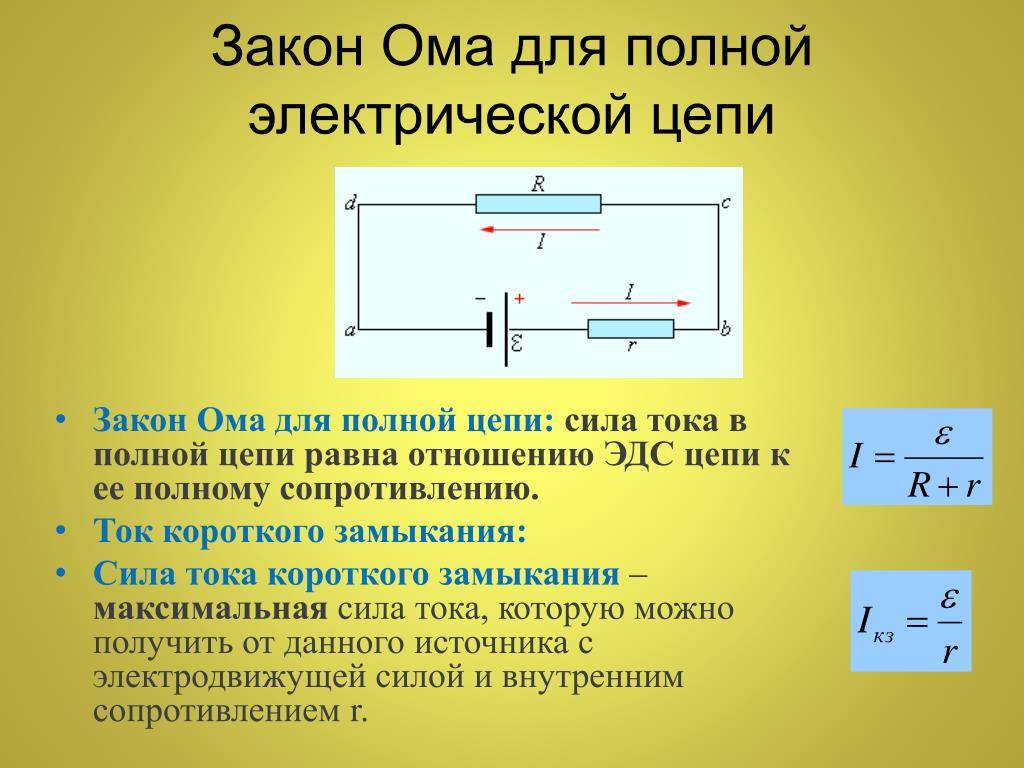
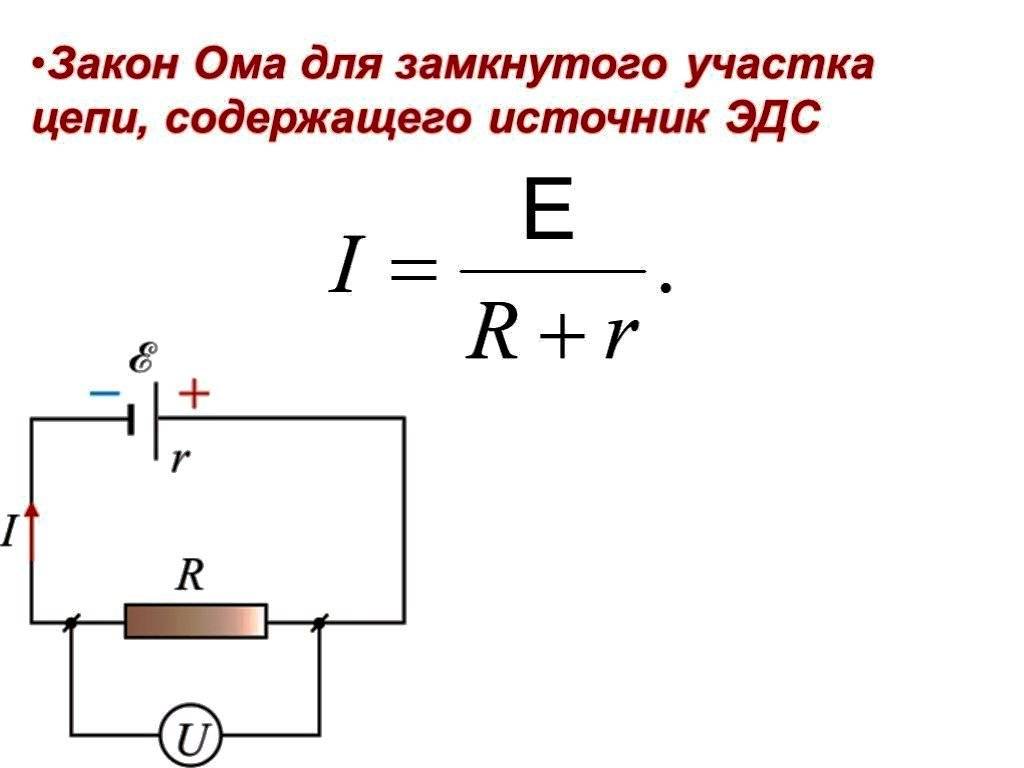
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Электрический ток
Мы выяснили, что подвижные носители зарядов в проводнике перемещаются под действием внешнего электрического поля, пока не выровняются потенциалы всех точек проводника. Однако если в двух точках проводника каким-то образом искусственно поддерживать различные потенциалы, то это поле будет обеспечивать непрерывное движение зарядов: положительных — от точек с большим потенциалом к точкам с меньшим потенциалом, а отрицательных — наоборот. Когда эта разность потенциалов не меняется со временем, то в проводнике устанавливается постоянный электрический ток.
Вспомним из курса физики некоторые сведения об электрическом токе.
Упорядоченное движение свободных зарядов в проводнике называется электрическим током проводимости, или электрическим током. Основными условиями существования электрического тока являются:
- наличие свободных заряженных частиц;
- наличие источника тока, создает электрическое поле, действие которого приводит упорядоченное движение свободных заряженных частиц;
- замкнутость электрической цепи, которая обеспечивает циркуляцию свободных заряженных частиц.
В зависимости от величины удельного сопротивления, который вещества оказывают постоянному току, они делятся на проводники, полупроводники, диэлектрики.
В зависимости от среды различают особенности прохождения электрического тока, в частности в металлах, жидкостях и газах, где носителями тока могут быть свободные электроны, положительные и отрицательные ионы.
Направление движения электронов
Полная электрическая цепь содержит источник тока и электроприборы, а также устройство для замыкания (размыкания) электрической цепи. За направление тока в цепи условно выбирают направление от положительного полюса источника тока к отрицательному (реальное движение носителей тока — электронов — происходит в обратном направлении).
Основными физическими величинами, характеризующими электрический ток, являются следующие:
Сила тока I — физическая величина, характеризующая скорость перераспределения электрического заряда в проводнике и определяется отношением заряда q, проходящий через любой сечение проводника за время t, к величине этого интервала времени, I=q/t. Единица силы тока — ампер, 1А =1Кл/сек.
Электрическое сопротивление R — это физическая величина, характеризующая свойство проводника противодействовать прохождению электрического тока. Единица электрического сопротивления — ом, 1 Ом.
Сопротивление проводника зависит от его физических параметров — длины l, площади поперечного сечения S и от удельного сопротивления вещества p, из которой он изготовлен: R = р*l/S.
И как мы знаем, образования тока в проводнике обуславлено наличием разности потенциалов ϕ 1 – ϕ 2 , которую еще называют напряжением.
Напряжение U — это физическая величина, определяемая работой электрического поля по перемещению единичного положительного заряда между двумя точками поля, U = A/q. Единица напряжения — вольт, 1 В.
Закон Ома для цепи
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Закон Ома для участка цепи.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит: Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Кулон и электрический заряд
Одна из основных единиц электрических измерений, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, – это кулон – единица измерения электрического заряда, пропорциональная количеству электронов в несбалансированном состоянии. Один кулон заряда соответствует 6 250 000 000 000 000 000 электронов. Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.
Как указывалось ранее, напряжение – это мера потенциальной энергии на единицу заряда, доступная для стимулирования протекания тока из одной точки в другую. Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.
Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.
Переменный ток
Мы уже рассмотрели закон Ома для всей цепи для постоянного тока. Как же изменится формула при переменном токе? Прежде чем мы это узнаем, давайте охарактеризуем само понятие. Переменный ток – это движение электрически заряженных частиц, направление и значение которых изменяется с течением времени. В отличие от постоянного он сопровождается дополнительными факторами, порождающими новый вид сопротивления (реактивного). Свойственно оно конденсаторам и катушкам индуктивности.

Закон Ома для полной цепи для переменного тока имеет вид:
I = U / Z,
где Z – комплексное сопротивление, состоящее из активных и реактивных.
ФИЗИКА
§ 2.9. Закон Ома для электрической цепи переменного тока
Рассмотрим теперь более общий случай электрической цепи, в которой последовательно соединены проводник с активным сопротивлением R и малой индуктивностью, катушка с большой индуктивностью L и малым активным сопротивлением и конденсатор емкостью С (рис. 2.20).
Рис. 2.20
Чему равна амплитуда силы тока в такой цепи (колебательном контуре), если на ее концах поддерживается напряжение u(t) = U sin ωt?
Мы видели, что при включении по отдельности в цепь проводника с активным сопротивлением R, конденсатора емкостью С или катушки с индуктивностью L амплитуда силы тока определяется соответственно формулами (2.6.2), (2.7.3) и (2.8.4). Амплитуды же напряжений на резисторе, катушке индуктивности и конденсаторе связаны с амплитудой силы тока так:
В цепях постоянного тока напряжение на концах цепи равно сумме напряжений на отдельных последовательно соединенных участках цепи. Однако, если измерить результирующее напряжение на контуре и напряжения на отдельных элементах цепи переменного тока, окажется, что напряжение на контуре (действующее значение) не равно сумме напряжений на отдельных элементах.
Почему это так? Дело в том, что гармонические колебания напряжения на различных участках цепи сдвинуты по фазе друг относительно друга.
Действительно, квазистационарный ток в любой момент времени одинаков во всех участках цепи. Это значит, что одинаковы амплитуды и фазы токов, протекающих по участкам с емкостным, индуктивным и активным сопротивлением. Однако только на участке с активным сопротивлением колебания напряжения и силы тока совпадают по фазе. На конденсаторе колебания напряжения отстают по фазе от колебаний силы тока на π/2 (см. § 2.7), а на катушке индуктивности колебания напряжения опережают колебания силы тока на π/2 (см. § 2.8).
Векторная диаграмма электрической цепи
Для вывода закона Ома в случае электрической цепи переменного тока, изображенной на рисунке 2.20, нужно уметь складывать мгновенные колебания напряжений, сдвинутых по фазе друг относительно друга. Проще всего выполнять сложение нескольких гармонических колебаний с помощью векторных диаграмм, о которых было рассказано в § 1.11. Векторная диаграмма электрических колебаний в цепи позволит нам определить амплитуду силы тока в зависимости от амплитуды напряжения и сдвиг фаз между силой тока и напряжением.
Так как сила тока одинакова во всех участках цепи, то построение векторной диаграммы удобно начать с вектора силы тока m. Этот вектор изобразим в виде вертикальной стрелки (рис. 2.21). Напряжение на резисторе совпадает по фазе с силой тока. Поэтому вектор mR должен совпадать по направлению с вектором m. Его модуль равен UmR = ImR.
Рис. 2.21
Колебания напряжения на катушке индуктивности опережают колебания силы тока на π/2 и соответствующий вектор и mL должен быть повернут относительно вектора m на π/2. Его модуль равен UmL = IωL. Если считать, что положительному сдвигу фаз соответствует поворот вектора против часовой стрелки, то вектор mL следует повернуть налево на π/2. (Можно было бы, конечно, поступить и наоборот.)
Вектор напряжения на конденсаторе mC отстает по фазе от вектора m на π/2 и поэтому повернут на этот угол относительно вектора m направо. Его модуль равен .
Для нахождения вектора суммарного напряжения m нужно сложить три вектора: mR, mL и mC. Вначале удобнее сложить два вектора mL и mC (рис. 2.22).
Рис. 2.22
Модуль этой суммы равен , если . Именно такой случай изображен на рисунке. После этого, сложив вектор mL + mC с вектором mR, получим вектор m, характеризующий колебания напряжения в сети.
По теореме Пифагора (из треугольника АОВ):
или
Из равенства (2.9.2) можно найти амплитуду силы тока в цепи:
Это и есть закон Ома для электрической цепи переменного тока, изображенной на рисунке 2.20.
Благодаря сдвигу фаз между напряжениями на различных участках цепи полное сопротивление Z цепи (см. рис. 2.20) выражается так:
От амплитуд силы тока и напряжения можно перейти к действующим значениям этих величин. Они связаны друг с другом точно так же, как и амплитуды в формуле (2.9.3):
Мгновенное значение силы тока меняется со временем гармонически:
где φc, — разность фаз между силой тока и напряжением в сети. Она зависит от частоты со и параметров цепи R, L, С.
Сдвиг фаз между током и напряжением
Сдвиг фаз φc, между колебаниями силы тока и напряжения равен по модулю углу φ между векторами m и m (см. рис. 2.22). Как следует из этого рисунка,
Согласно рисунку 2.22, сила тока отстает от напряжения по фазе при условии . Поэтому сдвиг фаз φc = -φ и
В частных случаях цепей с активным, емкостным и индуктивным сопротивлениями из этой формулы получаются правильные значения сдвига фаз.
Ограничения закона Ома:
- Имейте в виду, что закон Ома не может применяться к односторонним сетям – эти сети содержат односторонние элементы, включая диоды, транзисторы и т. Д., Что означает, что эти элементы не имеют одинакового отношения напряжения к току для обоих направлений тока.
- Оптимистические исследования показывают, что закон Ома не применяется к нелинейным элементам – это элементы, у которых ток не прямо пропорционален приложенному напряжению, что означает, что значение сопротивления этих элементов изменяется для разных значений напряжения и расчет тока по мощности. Примеры нелинейных элементов: тиристор, электрическая дуга и т. Д.
Электрические цепи и их разновидности
Электрическая цепь представляет собой комплекс устройств и отдельных объектов, которые связываются заданным способом. Они обеспечивают путь для прохождения электротока. Для характеристики отношения заряда, протекающего в рамках каждого отдельного проводника за некоторое время, к продолжительности этого времени используется определенная физическая величина. И это сила тока в электрической цепи.
В состав такой цепи включены источник энергии, энергопотребители, т.е. нагрузка и провода. Они делятся на две разновидности:
- Неразветвленные – ток, движущийся от генератора к энергопотребителю, не меняется по своему значению. Например, это освещение, включающее в свой состав только одну лампочку.
- Разветвленные – цепи, имеющие некоторые ответвления. Ток, двигаясь от источника, разделяется и идет на нагрузку по нескольким ветвям. При этом его значение меняется.
Примером может служить освещение, включающее многорожковую люстру.
Ветвь являет собой один или несколько компонентов, соединенных последовательно. Движение тока идет от узла с высоким напряжением к узлу с минимальным его значением. При этом входящий ток на узле совпадает с выходящим.
Цепи могут быть нелинейными и линейными. Если в первых существует один и более элементов, где есть зависимость значений от тока и напряжения, то у вторых характеристики элементов не имеют такой зависимости. Кроме того, в цепях, характеризующихся постоянным током, его направление не меняется, а при условии переменного тока происходит его изменение с учетом параметра времени .
Разбираемся что такое ток и сопротивление
Начнем с понятия электрического тока. Если говорить коротко, электрический ток применительно к металлам — это направленное движение электронов — отрицательно заряженных частиц. Их обычно представляют в виде небольших кружочков. В спокойном состоянии они передвигаются хаотически, постоянно меняя свое направление. При определенных условиях — возникновении разницы потенциалов — эти частицы начинают определенное движение в какую-то сторону. Вот это движение и есть электрический ток.
Чтобы было понятнее, можно сравнить электроны с водой, разлитой на какой-то плоскости. Пока плоскость неподвижна, вода не движется. Но, как только появился наклон (возникла разница потенциалов), вода пришла в движение. С электронами примерно так же.

Примерно так можно себе представить электрический ток
Теперь надо понять, что такое сопротивление и почему с силой тока у них обратная связь: чем выше сопротивление, тем меньше ток. Как известно, электроны движутся по проводнику. Обычно это металлические провода, так как металлы обладают хорошей способностью проводить электрический ток. Мы знаем, что металл имеет плотную кристаллическую решетку: много частиц, которые расположены близко и связаны между собой. Электроны, пробираясь между атомами металла, на них наталкиваются, что затрудняет их движение. Это помогает проиллюстрировать сопротивление, которое оказывает проводник. Вот теперь становится понятным, почему, чем выше сопротивление, тем меньше сила тока — чем больше частиц, тем электронам сложнее преодолевать путь, делают они это медленнее. С этим, вроде, разобрались.
Если у вас есть желание проверить эту зависимость опытным путем, найдите переменный резистор, соедините последовательно резистор — амперметр — источник тока (батарейка). Еще желательно в цепь вставить выключатель — обычный тумблер.

Цепь для проверки зависимости силы тока от сопротивления
Крутя ручку резистора вы изменяете сопротивление. При этом показания на амперметре, который измеряет силу тока, тоже меняются. Причем чем больше сопротивление, тем меньше отклоняется стрелка — меньше ток. Чем сопротивление меньше — тем сильнее отклоняется стрелка — ток больше.
Зависимость тока от сопротивления почти линейная, то есть на графике отражается почти прямой линией. Почему почти — об этом надо говорить отдельно, но это другая история.