В цепи переменного тока с индуктивностью колебания напряжения 1

Сопротивление в цепи при переменном напряжении

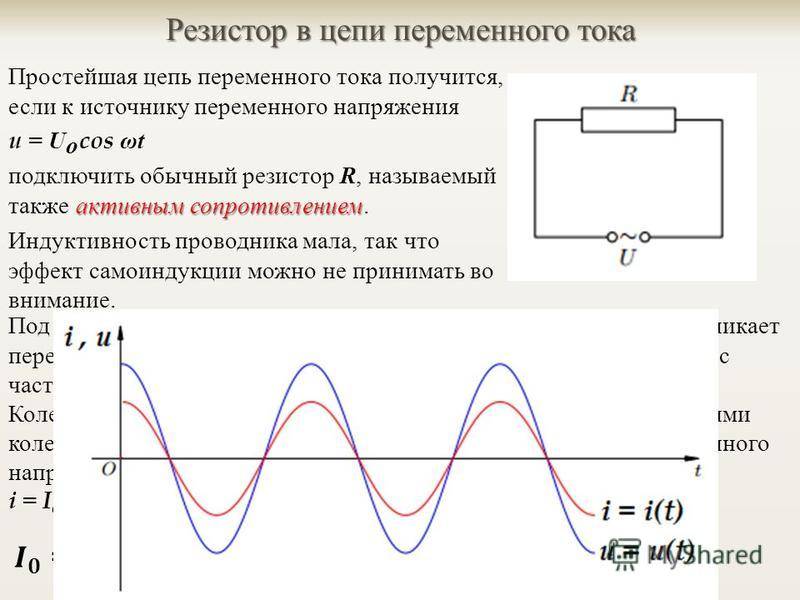
Цепи переменного напряжения с сопротивлением является самыми простыми и наиболее часто встречающимися, поэтому начнём с них.

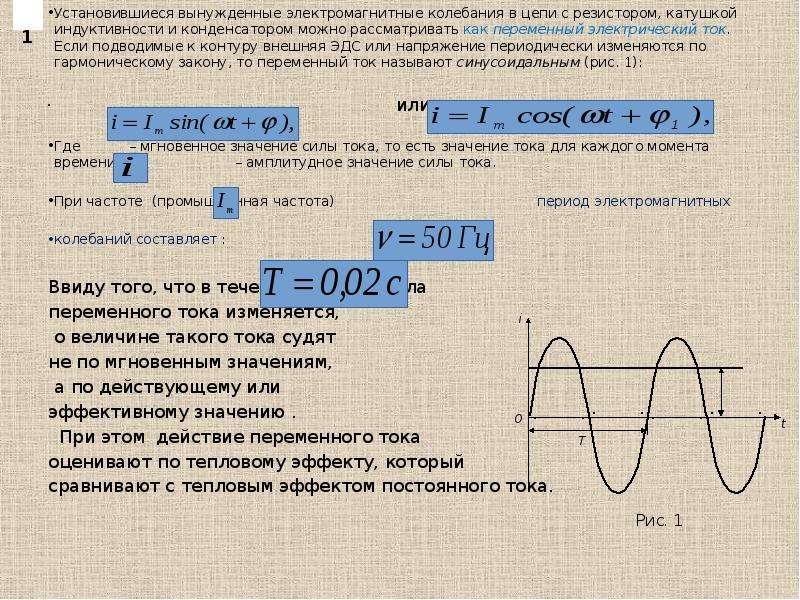
Переменное синусоидальное напряжение и ток в сопротивлении.

Допустим, что на сопротивление R подали переменное напряжение u, тогда, согласно с законом Ома, через данное сопротивление потечёт электрический ток i

где U_m – амплитудное значение переменного напряжения,

I_m – амплитудное значение переменного тока,

ω – угловая частота,

t – время,

φ – начальная фаза

Таким образом, действующее I и среднее значение I_cp переменного тока будут определяться следующими выражениями

Так как, напряжение и ток, в цепи с сопротивлением имеют одинаковую начальную фазу, то есть, происходит совпадение фаз и достижение амплитудных значений напряжения U_m и тока I_m происходит одновременно.

Выражение «совпадение фаз» связанно с понятием фазового сдвига ψ, которое определяет разность начальных фаз двух синусоид одинаковой частоты. Следовательно, фазовый сдвиг между напряжением и током при активном сопротивлении будет равен нулю

где φ_u – начальная фаза напряжения,

φ_i – начальная фаза тока.

Для оценки энергетических характеристик ввели понятие мощности, в цепях переменного напряжения существует несколько мощностных характеристик. Одной из них является мгновенная мощность Р_m, определяемая, как произведение мгновенных значений напряжения и тока

где U_m – амплитудное значение переменного напряжения,

I_m – амплитудное значение переменного тока,

U – действующее значение переменного напряжения,

I – действующее значение переменного тока.

Таким образом, мгновенная мощность Р_m изменяется с удвоенной частотой по сравнению с частотой напряжения и тока и колеблется в пределах от 0 до 2UI.

Еще одной энергетической характеристикой является среднее значение мощности за период Р или активная мощность, которая определяется следующим выражением

где Р_m – мгновенная мощность,

U – действующее значение переменного напряжения,

I – действующее значение переменного тока.

Конденсатор в цепи переменного тока

Рассмотрим процессы, протекающие в электрической цепи переменного тока с конденсатором. Если подключить конденсатор к источнику постоянного тока, то в цепи возникнет кратковременный импульс тока, который зарядит конденсатор до напряжения источника, а затем ток прекратится. Если заряженный конденсатор отключить от источника постоянного тока и соединить его обкладки с выводами лампы накаливания, то конденсатор будет разряжаться, при этом наблюдается кратковременная вспышка лампы.

При включении конденсатора в цепь переменного тока процесс его зарядки длится четверть периода. После достижения амплитудного значения напряжение между обкладками конденсатора уменьшается и конденсатор в течение четверти периода разряжается. В следующую четверть периода конденсатор вновь заряжается, но полярность напряжения на его обкладках изменяется на противоположную и т.д. Процессы зарядки и разрядки конденсатора чередуются с периодом, равным периоду колебаний приложенного переменного напряжения.

Как и в цепи постоянного тока, через диэлектрик, разделяющий обкладки конденсатора, электрические заряды не проходят. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора по проводам, соединенным с его выводами, течет переменный ток. Лампа накаливания, включенная последовательно с конденсатором в цепь переменного тока (рис. 6), кажется горящей непрерывно, так как человеческий глаз при высокой частоте колебаний силы тока не замечает периодического ослабления свечения нити лампы.

Рис. 6

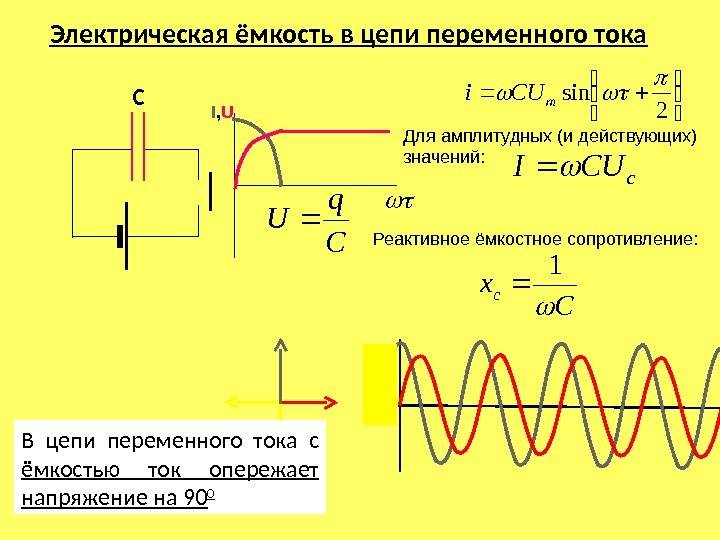
Установим связь между амплитудой колебаний напряжения на обкладках конденсатора и амплитудой колебаний силы тока. При изменениях напряжения на обкладках конденсатора по гармоническому закону

\(~u = U_m \cdot \cos \omega t\) ,

заряд на его обкладках изменяется по закону:

\(~q = C \cdot u = U_m \cdot C \cdot \cos \omega t\) .

Электрический ток в цепи возникает в результате изменения заряда конденсатора: i = q’. Поэтому колебания силы тока в цепи происходят по закону:

\(~i = -U_m \cdot \omega \cdot C \cdot \sin \omega t = U_m \cdot \omega \cdot C \cdot \cos (\omega t + \frac{\pi}{2})\) .

Следовательно, колебания напряжения на обкладках конденсатора в цепи переменного тока отстают по фазе от колебаний силы тока на π/2 или колебания силы тока опережают по фазе колебания напряжения на π/2 (рис. 7). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того как напряжение достигает максимума, сила тока становится равной нулю и т.д.

Рис. 7

Произведение \(U_m \cdot \omega \cdot C\) является амплитудой колебаний силы тока:

\(~I_m = U_m \cdot \omega \cdot C\) .

Отношение амплитуды колебаний напряжения на конденсаторе к амплитуде колебаний силы тока называют емкостным сопротивлением конденсатора (обозначается Х_C):

\(~X_C = \frac{U_m}{I_m} = \frac{1}{\omega \cdot C}\) .

Связь между амплитудным значением силы тока и амплитудным значением напряжения по форме совпадает с выражением закона Ома для участка цепи постоянного тока, в котором вместо электрического сопротивления фигурирует емкостное сопротивление конденсатора:

\(~I_m = \frac{U_m}{X_C}\) .

Емкостное сопротивление конденсатора, как и индуктивное сопротивление катушки, не является постоянной величиной. Оно обратно пропорционально частоте переменного тока. Поэтому амплитуда колебаний силы тока в цепи конденсатора при постоянной амплитуде колебаний напряжения на конденсаторе возрастает прямо пропорционально частоте.

Закон Ома для участка цепи с конденсатором

Для неизменного сигнала конденсатор представляет непреодолимое препятствие. Переменный сигнал проходит через него с некоторым усилием. Называют его емкостным сопротивлением.

Оно зависит от электроемкости конденсатора, частоты сигнала и обратно пропорционально произведению:

Обозначения:

• RC – емкостное сопротивление;
• ω – круговая частота;
• C – емкость конденсатора.

Зависимость величин для участка цепи с конденсатором записывают так:

Конденсатор – реактивная нагрузка. Колебания напряжения, скорости изменения заряда не синхронны. Изменение U отстает от колебаний I на четверть периода:

Сдвиг фаз составляет 90°. Индуктивные, емкостные нагрузки сдвигают фазу в противоположных направлениях.

Характеристики и свойства

К параметрам конденсатора, которые используют для создания и ремонта электронных устройств, относят:

1. Ёмкость — С. Определяет количество заряда, которое удерживает прибор. На корпусе указывается значение номинальной ёмкости. Для создания требуемых значений элементы включают в цепь параллельно или последовательно. Эксплуатационные величины не совпадают с расчетными.
2. Резонансная частота — fр. Если частота тока больше резонансной, то проявляются индуктивные свойства элемента. Это затрудняет работу. Чтобы обеспечить расчетную мощность в цепи, конденсатор разумно использовать на частотах меньше резонансных значений.
3. Номинальное напряжение — Uн. Для предупреждения пробоя элемента рабочее напряжение устанавливают меньше номинального. Параметр указывается на корпусе конденсатора.
4. Полярность. При неверном подключении произойдет пробой и выход из строя.
5. Электрическое сопротивление изоляции — Rd. Определяет ток утечки прибора. В устройствах детали располагаются близко друг к другу. При высоком токе утечки возможны паразитные связи в цепях. Это приводит к неисправностям. Ток утечки ухудшает емкостные свойства элемента.
6. Температурный коэффициент — TKE. Значение определяет, как ёмкость прибора меняется при колебаниях температуры среды. Параметр используют, когда разрабатывают устройства для эксплуатации в тяжелых климатических условиях.
7. Паразитный пьезоэффект. Некоторые типы конденсаторов при деформации создают шумы в устройствах.

Особенности переменного напряжения, тока

Генераторы, вырабатывающие электроэнергию, сконструированы так, что напряжение, скорость изменения заряда в наших линиях электропередач меняются по гармоничному закону:

Обозначения:

• u, i – мгновенные значения (в произвольный момент времени);
• Um, Im – амплитудные значения (максимальные);
• Um – амплитуда напряжения;
• Im – амплитуда тока;
• t – время;
• величина ω – циклическая частота.

Величина ω связана с линейной частотой ν выражением:

• π = 3,14 – математическая константа;
• ν = 50 Гц (для электрических сетей в нашей стране).

Произведение ωt называют фазой:

Измеряют в радианах (рад), φ0 – начальная фаза, зачастую равна нулю. Использование в формулах функции cos не изменяет смысла физических выражений.

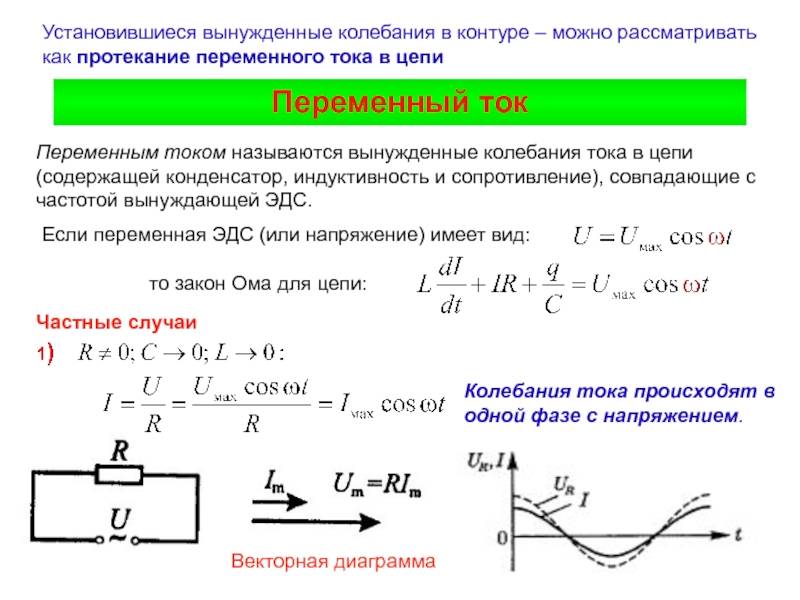
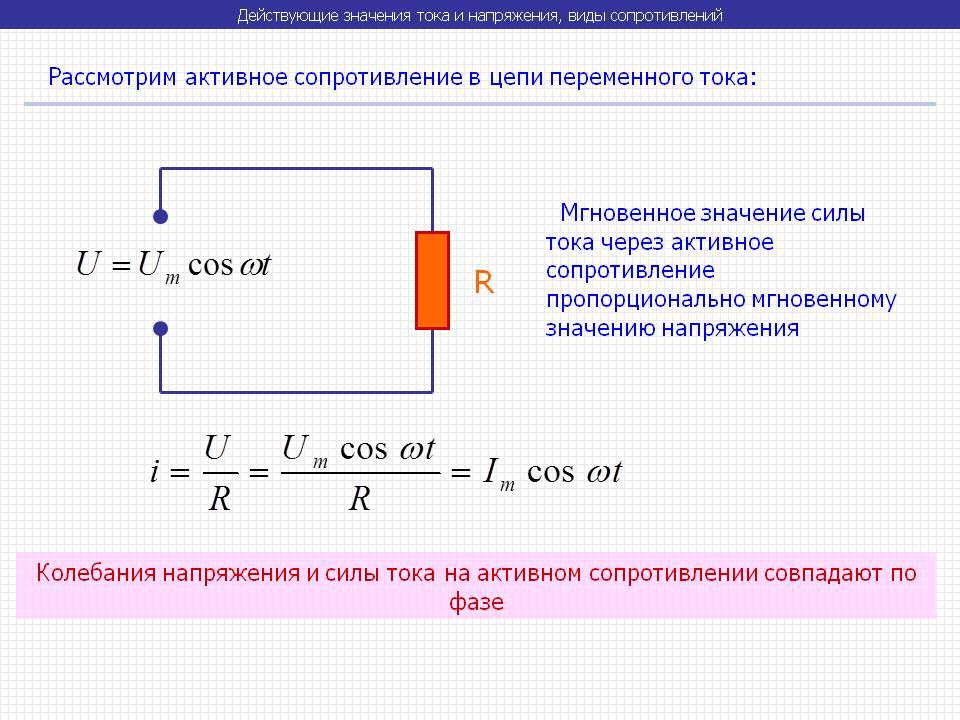
Если напряжение, изменяющееся по гармоничному закону, приложить к обычному резистору (в его роли может быть лампа накаливания, тепловой нагреватель), то через него начнут двигаться частицы, характер движения которых изменяется по такому же закону.

Изменение величин будет синхронным, фазы – одинаковыми. Такое сопротивление называют активным.

Метод векторных диаграмм

Мы уже пользуемся векторными диаграммами, по которым наблюдаем соотношения токов и напряжения в цепях переменного тока. Векторная диаграмма это стоячее изображение вращающихся векторов.

В предыдущих рассуждениях, было сказано, что линейно развернутая диаграмма переменного процесса, (в простом случае синусоидального), точно показывает  изменение мгновенного значения переменной величины, то есть происходит все именно так как показывает синусоида и каждая ее точка и есть переменная величина в данный момент. Но оказывается нам интересно не это, нам нужно знать какое значение тока и напряжения и мощности действует в цепи в течение времени, то есть действует длительное время, пока цепь работает.

Анализ синусоид нескольких величин, одновременно действующих в разных фазах, позволяет рассчитать все свойства и режимы работы цепи переменного тока, но гораздо проще это сделать, если отвлечься от синусоид и просто построить соотношение векторов, которые, собственно, и образуют эти синусоиды. Вся информация синусоид заложена в их радиус – векторах. Мы останавливаем эти векторы на рисунке, понимая, что они вращающиеся, но факт их вращения учитываем угловой частотой в расчетных формулах векторной диаграммы.

Итак, векторная диаграмма заменяет линейно развернутую синусоидальную диаграмму, потому, что любая информация, заложенная в синусоиду, есть и в соответствующем ей радиус-векторе.

Если нам приходится рассматривать несколько действующих одновременно синусоидальных процессов, то они изображаются векторной диаграммой, где длина каждого вектора, соответствует действующему значению синусоидальной величины, направление вектора соответствует начальной фазе, синусоидальной величины.

Результирующие значения одновременно действующих напряжений рассчитывается как векторная сумма, где угол между векторами определяется сдвигом фаз между ними.

Расчет цепей переменного тока сводится к расчету треугольников, которые состоят из соответствующих векторов.

Например, можно определить суммарное напряжение, частичные напряжения, и сдвиг фаз между ними.

На основании векторных диаграмм можно построить подобные векторным диаграммам треугольники сопротивлений и треугольники мощностей, решением которых можно определить соотношения сопротивлений, и мощности которые действуют в цепях переменного тока.

Векторная диаграмма напряжений представляет собой векторный треугольник напряжений

Последовательное соединение L R.

Любая катушка наматывается проволокой, а проволока обладает сопротивлением, которое приходится учитывать.

Получается, что реальная цепь, содержащая только L, просто невозможна. В некоторых случаях значением R пренебрегают, и получается, что вроде бы цепь с только L, на самом деле она конечно L R.

Реально, кроме проволоки, в цепи всегда есть и какие – то другие элементы R, поэтому интерес представляют именно цепи L R,

Ток, при последовательном соединении, один и тот же через все сопротивления, а напряжения разные, но общее напряжение не равно просто сумме напряжений на каждом сопротивлении, оно равно векторной сумме, то есть вектор общего напряжения равен сумме векторов напряжений на каждом участке. Для расчетов напряжений надо построить векторную диаграмму.

Векторная диаграмма строится так.

Виды конденсаторов

Емкостные элементы классифицируют по типу диэлектрика, применяемого в конструкции.

Бумажные и металлобумажные конденсаторы

Элементы используются в цепях с постоянным или слабо пульсирующим напряжением. Простота конструкции оборачивается пониженной на 10-25% стабильностью характеристик и возросшей величиной потерь.

В бумажных конденсаторах обкладки из алюминиевой фольги разделяет бумага. Сборки скручивают и помещают в корпус в форме цилиндра или прямоугольного параллелепипеда.

Приборы работают при температурах -60…+125°C, с номинальным напряжением у низковольтных приборов до 1600 В, высоковольтных — выше 1600 В и ёмкостью до десятков мкФ.

В металлобумажных приборах вместо фольги на диэлектрическую бумагу наносят тонкий слой металла. Это помогает изготовить элементы меньших размеров. При незначительных пробоях возможно самовосстановление диэлектрика. Металлобумажные элементы уступают бумажным по сопротивлению изоляции.

Электролитические конденсаторы

Конструкция изделий напоминает бумажные. Но при изготовлении электролитических элементов бумагу пропитывают оксидами металлов.

В изделиях с электролитом без бумаги оксид наносится на металлический электрод. У оксидов металлов односторонняя проводимость, что делает прибор полярным.

В некоторых моделях электролитических элементов обкладки изготавливают с канавками, которые увеличивают площадь поверхности электрода. Зазоры в пространстве между пластинами устраняют с помощью заливания электролитом. Это улучшает емкостные свойства изделия.

Большая ёмкость электролитических приборов — сотни мкФ, используется в фильтрах, чтобы сглаживать пульсации напряжения.

Алюминиевые электролитические

В приборах этого типа анодная обкладка делается из алюминиевой фольги. Поверхность покрывают оксидом металла — диэлектриком. Катодная обкладка — твердый или жидкий электролит, который подбирается так, чтобы при работе восстанавливался слой оксида на фольге. Самовосстановление диэлектрика продлевает время работы элемента.

Конденсаторы такой конструкции требуют соблюдения полярности. При обратном включении разорвет корпус.

Приборы, внутри которых располагаются встречно-последовательные полярные сборки, используют в 2 направлениях. Ёмкость алюминиевых электролитических элементов достигает нескольких тысяч мкФ.

Танталовые электролитические

Анодный электрод таких приборов изготовляют из пористой структуры, получаемой при нагреве до +2000°C порошка тантала. Материал внешне напоминает губку. Пористость увеличивает площадь поверхности.

С помощью электрохимического окисления на анод наносят слой пентаоксида тантала толщиной до 100 нанометров. Твердый диэлектрик делают из диоксида марганца. Готовую конструкцию прессуют в компаунд — специальную смолу.

Танталовые изделия используют на частотах тока свыше 100 кГц. Ёмкость создается до сотен мкФ, при рабочем напряжении до 75 В.

Полимерные

В конденсаторах используются электролит из твердых полимеров, что дает ряд преимуществ:

• увеличивается срок эксплуатации до 50 тыс. часов;
• сохраняются параметры при нагреве;
• расширяется диапазон допустимых пульсаций тока;
• сопротивление обкладок и выводов не шунтирует ёмкость.

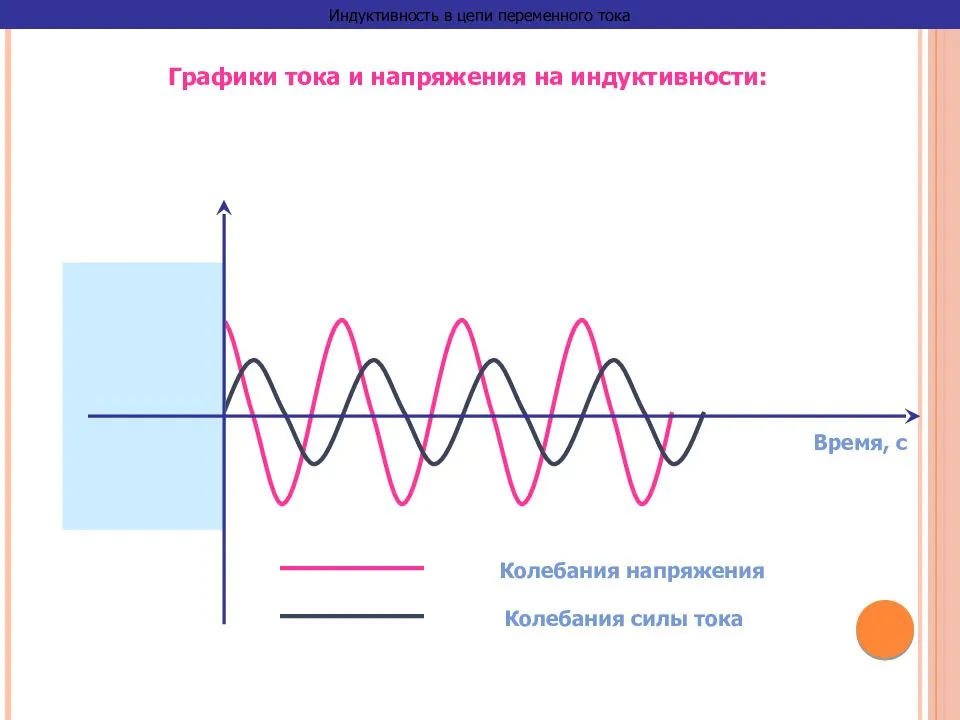
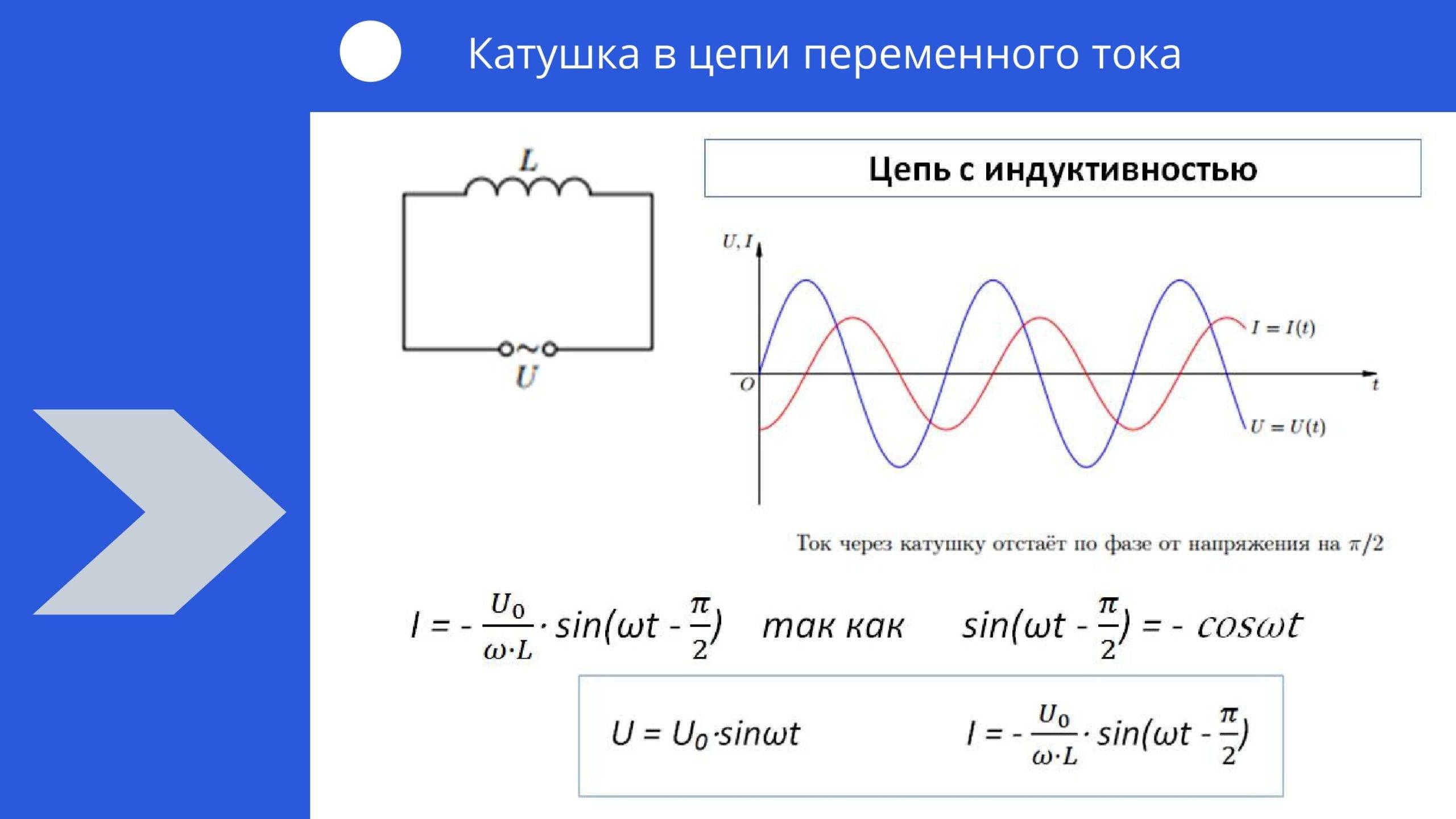
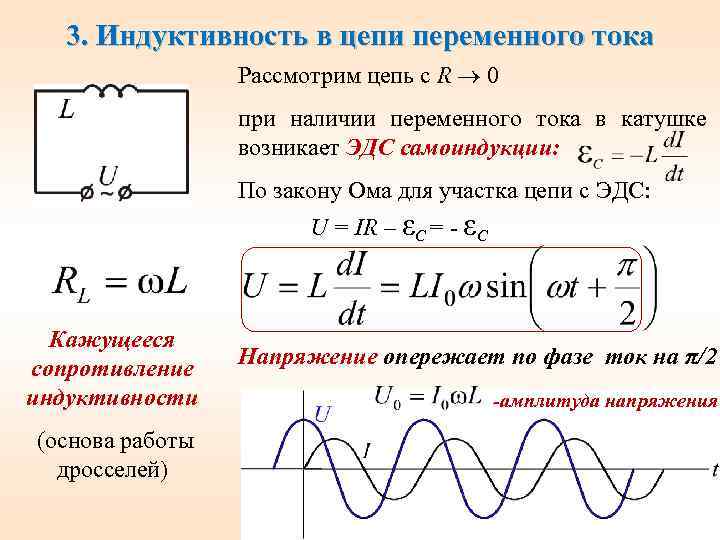
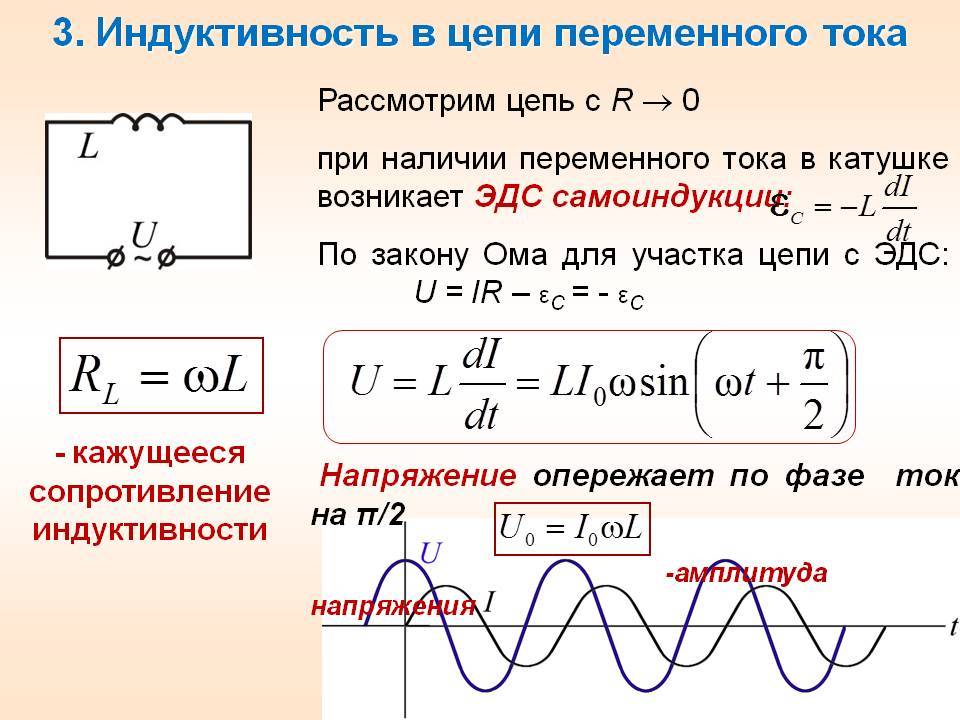
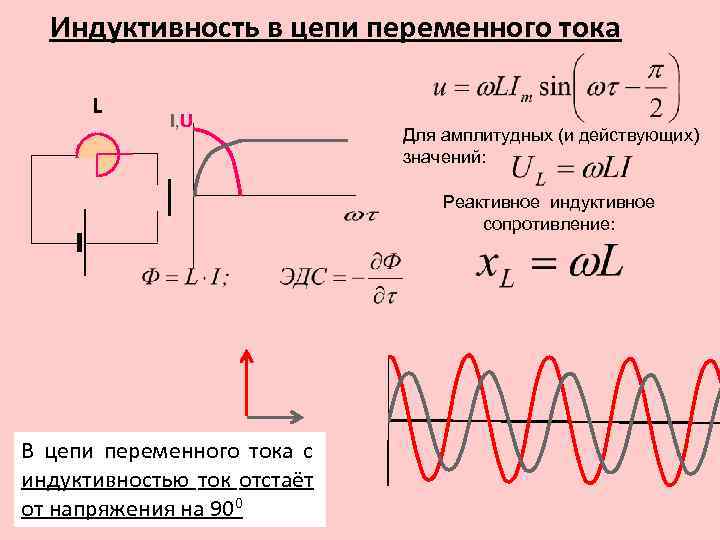
Индуктивное сопротивление в цепи переменного тока

X_L = ωL     

Чтобы сделать сосредоточенную индуктивность, кусок проволоки сматывают в катушку

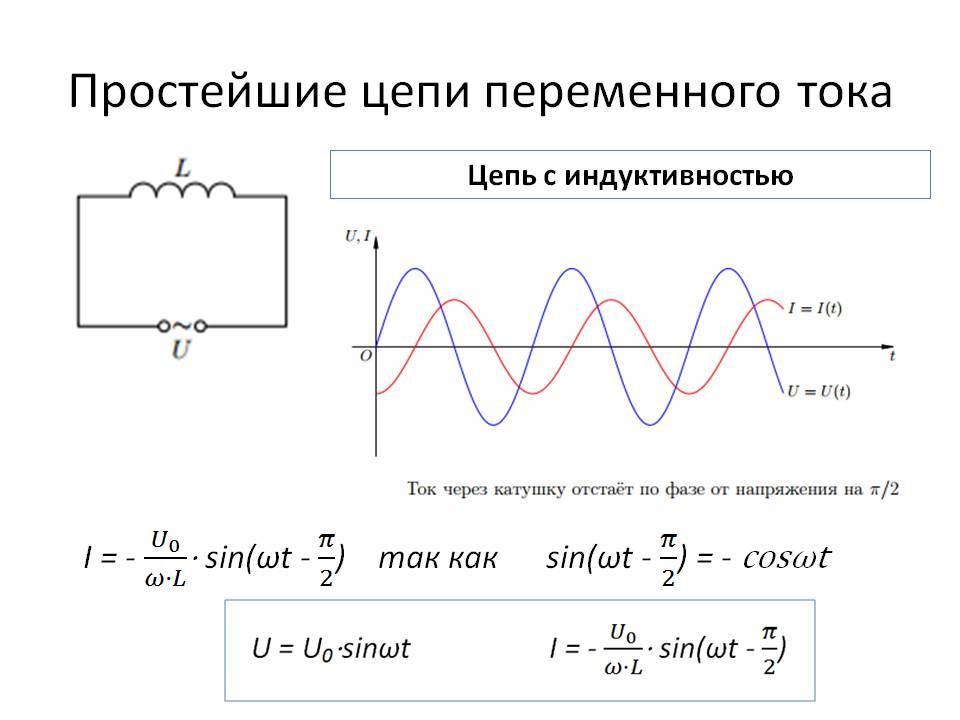
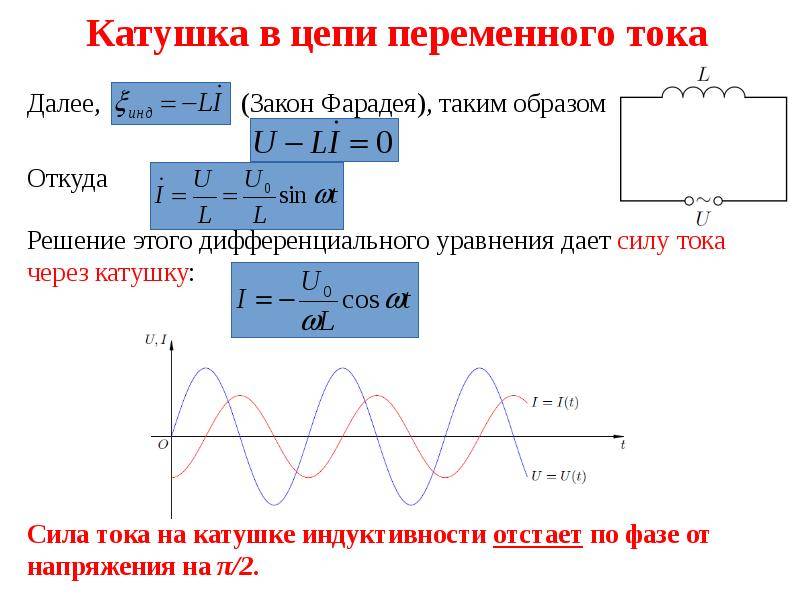
Если к цепи с индуктивностью подключить переменное синусоидальное напряжение, то в ней должен протекать переменный синусоидальный ток.

Что же происходит в цепи с индуктивностью при протекании переменного тока.

Оказывается, ток и напряжение действуют не одновременно,

то есть, сдвинуты по фазе

На активном сопротивлении R, появление напряжения, и сразу – в тот же момент,  оно вызывает появление тока, и они действуют в одной фазе.

На индуктивности так не получается.

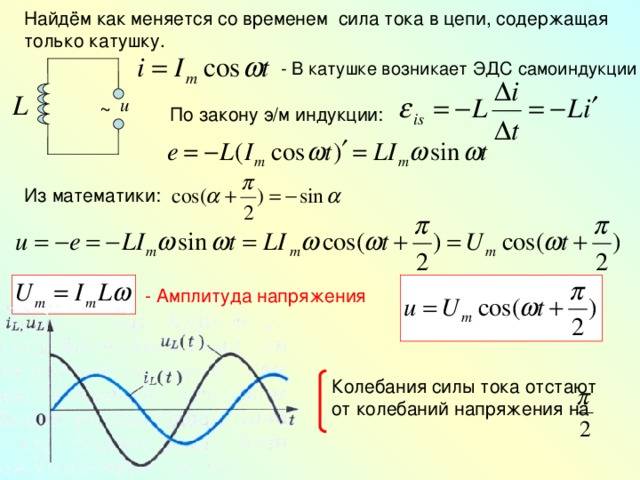
Если напряжение от источника начинает нарастать, то ток за ним не успевает.

Почему? В индуктивности изменение тока, приводит к появлению ЭДС самоиндукции, а эта ЭДС направлена на встречу изменения тока. Напряжение растет, и ток хочет расти, но ЭДС самоиндукции препятствует нарастанию тока. Это примерно также, как сила инерции мешает разогнать тележку, когда мы сдвигаем ее с места.

Ток преодолевает сопротивление направленной навстречу ему ЭДС самоиндукции, и начинает нарастать, но это происходит, когда напряжение уже достигло максимального значения. Ток, наконец, достигает максимального значения, но напряжение в этот момент уже снизилось до нуля. Так и повторяется – ток все время отстает от напряжения на 90то есть на π/2. Значит, фаза тока отрицательна и составляет  – π/2 

Откуда берется эта ЭДС самоиндукции, и почему она не мешает в цепи с сопротивлением  R. Это связано с тем, что катушка индуктивности, в отличие от сопротивления R, создает сильное магнитное поле, благодаря большому количеству витков. Магнитное поле не может мгновенно изменяться, оно и рождает внутри провода ЭДС, которая препятствует изменению тока.

Более подробно об ЭДС самоиндукции смотри в статье  Начальные представления об электромагнетизме

Красная синусоида напряжения пресекает ноль каждый раз раньше зеленой синусоиды тока на π/2 

Вывод: В цепи с индуктивностью напряжение впереди тока на 90°.

Любое сопротивление ограничивает ток, но бывает активное сопротивление, бывает реактивное..

R – активное сопротивление – на нем выделяется тепло

X – реактивное сопротивление на нем  не выделятся тепло

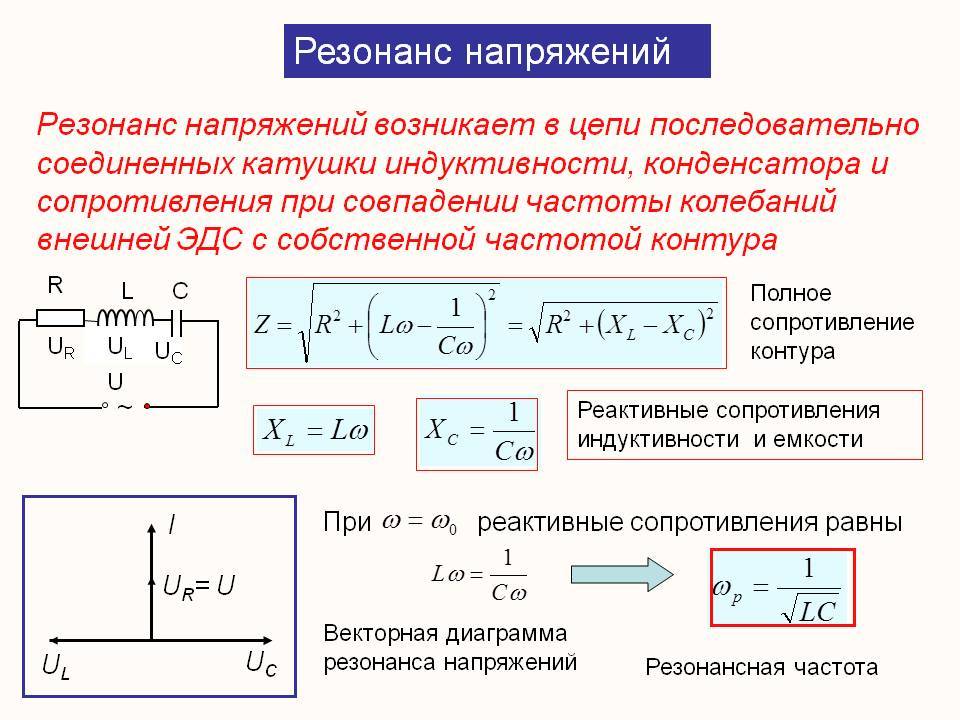
Резонанс напряжений

Давайте возьмем другие параметры катушки и конденсатора и посмотрим, что у нас происходит на самих радиоэлементах. Нам ведь надо досконально все выяснить ;-). Беру катушку индуктивности с индуктивностью в 22 микрогенри:

и конденсатор в 1000 пФ

Из них собираю последовательный колебательный контур. Итак, чтобы поймать резонанс, я не буду в схему добавлять резистор. Поступлю более хитрее.

Так как мой генератор частоты китайский и маломощный, то при резонансе у нас в цепи остается только активное сопротивление потерь R. В сумме получается все равно маленькое значение сопротивления, поэтому ток при резонансе достигает максимальных значений. В результате этого, на внутреннем сопротивлении генератора частоты падает приличное напряжение и выдаваемая амплитуда частоты генератора  падает. Я буду ловить минимальное значение этой амплитуды. Следовательно это и будет резонанс колебательного контура. Перегружать генератор — это не есть хорошо, но что не сделаешь ради науки!

Ну что же, приступим ;-). Давайте сначала посчитаем  резонансную частоту по формуле Томсона. Для этого я открываю онлайн калькулятор на просторах интернета и быстренько высчитываю эту частоту. У меня получилось 1,073 Мегагерц.

Ловлю резонанс на генераторе частоты по его минимальным значениям амплитуды. Получилось как-то вот так:

Размах амплитуды 4 Вольта

Хотя на генераторе частоты  размах  более 17 Вольт! Вот так вот сильно просело напряжение. И как видите, резонансная частота получилась чуток другая, чем расчетная: 1,109 Мегагерц.

Теперь небольшой прикол 😉

Вот этот сигнал мы подаем на наш последовательный колебательный контур:

Как видите, мой генератор не в силах выдать большую силу тока в колебательный контур на резонансной частоте, поэтому сигнал получился даже чуть искаженным на пиках.

Ну а теперь самое интересное. Давайте замеряем падение напряжения на конденсаторе и катушке на резонансной частоте. То есть это будет выглядеть вот так:

Смотрим напряжение на конденсаторе:

Размах амплитуды 20 Вольт (5х4)! Откуда? Ведь подавали мы на колебательный контур синус с частотой в 2 Вольта!

Ладно, может с осциллографом что-то произошло?. Давайте замеряем напряжение на катушке:

Народ! Халява!!! Подали 2 Вольта с генератора, а получили 20 Вольт и на катушке и на конденсаторе! Выигрыш энергии в 10 раз! Успевай только снимать энергию с конденсатора или с катушки!

Ну ладно раз такое дело… беру лампочку от мопеда на 12 Вольт и цепляю ее к конденсатору или катушке. Лампочке ведь вроде как по-барабану на какой частоте работать и какой ток кушать. Выставляю амплитуду, чтобы на катушке или конденсаторе было где то Вольт 20 так как среднеквадратичное напряжение будет где-то Вольт 14,  и цепляю поочередно к ним лампочку:

Как видите — полный ноль. Лампочка гореть не собирается, так что побрейтесь фанаты халявной энергии). Вы ведь не забыли, что мощность определяется произведением силы тока на напряжение? Напряжения вроде как-бы хватает, а вот силы тока — увы! Поэтому, последовательный колебательный контур носит также название узкополосного (резонансного) усилителя напряжения, а не мощности!

Объяснение резонанса напряжения

При резонансе напряжение на катушке и на конденсаторе оказались намного больше, чем то, которое мы подавали на колебательный контур. В данном случае у нас получилось в 10 раз больше. Почему же напряжение на катушке при резонансе равняется напряжению на конденсаторе. Это легко объясняется. Так как в последовательном колебательном контуре катушка и кондер идут друг за другом, следовательно, в цепи протекает одна и та же сила тока.

При резонансе реактивное сопротивление катушки равняется реактивному сопротивлению конденсатора. Получаем по правилу шунта, что на катушке у нас падает напряжение U_L = IX_L , а на конденсаторе U_C = IX_C . А так как при резонансе у нас X_L = X_C , то получаем что U_L = U_C , ток ведь в цепи один и тот же ;-). Поэтому резонанс в последовательном колебательном контуре называют также резонансом напряжений, так как напряжение на катушке на резонансной частоте равняется напряжению на конденсаторе.

Эффективные значения

Среднее арифметическое значение напряжения, скорости изменения заряда за период равно нулю, поэтому его нельзя использовать для характеристики колебательного процесса. Квадраты этих величин, их средние значения всегда положительны.

Квадрат среднего значения силы тока равен половине квадрата амплитудного значения:

Is – среднее значение. Его называют еще эффективным (другое название – действующим):

Квадрат силы тока пропорционален количеству энергии, образующейся в проводнике: Q ~ Is2.

Эффективное значение величины переменного тока равно величине постоянного, при котором за время t = T образуется такое же количество теплоты. Для действующего значения напряжения формула аналогична:

Именно эффективные значения показывают измерительные приборы.

Происхождение индуктивного сопротивления

Вокруг проводника с движущимися заряженными существует магнитное поле. Оно слабое, но магнитная стрелка на него реагирует.

Если проводник намотать на катушку, то магнитное поле станет значительно более сильным. Оно приводит к появлению в катушке еще одного вида тока. Его возникновение в проводнике под действием магнитного поля называют электромагнитной индукцией. Обмотку называют катушкой индуктивности, а движение зарядов – индукционным током.

Одно из проявлений электромагнитной индукции – самоиндукция: возникновение дополнительной ЭДС в моменты резких изменений силы тока.

Это не колебания, возбуждаемые генератором, а изменения в момент включения, выключения, короткого замыкания. Для явления справедлива формула:

Обозначения:

• Esi – ЭДС самоиндукции;
• ΔI – изменение силы тока;
• Δt – промежуток времени;
• L – индуктивность катушки, коэффициент самоиндукции.

Величина L – характеристика магнитных свойств катушки, измеряют ее в генри (Гн).

Индуктивность катушки равна 1 Гн, если при изменении в ней значения I на 1 А за 1 секунду возникает ЭДС самоиндукции 1 В.

Принцип работы конденсатора

Подключение прибора к постоянному источнику приводит к тому, что в начальный момент происходит аккумуляция в обкладках из-за электростатической индукции, а сопротивление в этот момент приравнивается нулю. Электрическая индукция провоцирует поле к притяжению разноимённых зарядов на разные обкладки, расположенные друг напротив друга.

Вам это будет интересно Периодичность замены электросчетчика

Такое свойство получило название ёмкость, которая характерна для всех типов материалов, в том числе и диэлектриков, однако в случае с проводниками она существенно больше. Именно поэтому обкладки изготавливаются из проводника. Увеличение ёмкости способствует накоплению большего количества зарядок на обкладках.

Важно! Когда аккумулируются заряды, происходят ослабление поля и наращивание двухполюсника. Принцип работы

Принцип работы

Происходит это из-за уменьшения места в обкладках, воздействия одноимённых зарядов друг на друга. Одновременно с этим напряжение приравнивается к источнику тока. Прекращение электричества в цепи происходит после того, когда обкладки полностью заполнятся электричеством. Из-за этого пропадает индукция и остаётся только поле, удерживающее и не пропускающее заряды.

Диэлектрик между обкладками

Электротоку будет некуда деться, а на двухполюснике напряжение приравнивается к ЭДС. Когда ЭДС повышается, поле сильнее воздействует на диэлектрик из-за отсутствия места в обкладках. Если внутреннее конденсаторное напряжение будет выше предельных значений, тогда пробьёт диэлектрик.

Конденсатор преобразуется в проводник, и происходит освобождение зарядов, из-за чего электроток начинает идти. Чтобы применять двухполюсник при высоком напряжении повышают размер диэлектрика и наращивают расстояние, имеющееся между обкладками на фоне снижения ёмкости. Диэлектрик располагается между обкладками и не даёт проходить постоянному, выполняя в отношении него барьерную функцию.

Электрическая индукция

Обратите внимание! Именно постоянное напряжение способно формировать электростатическую индукцию, но только в случае замыкания в момент зарядки конденсатора. Благодаря этому механизму сохраняется энергия до момента подсоединения к нему потребителю

Конденсатор в цепи постоянного тока

Чтобы понять, как работает накопитель в цепи постоянного тока, надо добавить в схему лампочку, которая станет загораться только при зарядке, в процессе которой от электротока остаётся напряжение, как бы догоняющее его из-за плавного нарастания. Заряды электричества затрачивают какое-то время для перемещения к обкладкам, именно это и есть время зарядки, продолжительность которого определяется частотой и ёмкостью напряжения. Когда зарядка завершается, лампочка тухнет, и постоянный электроток перестаёт проходить через пассивный электронный компонент.

Конденсатор в цепи переменного тока

Если у источника изменить полярность, то это приведёт к разрядке конденсатора в цепи переменного тока и его повторной зарядке. Формируется постоянная электростатическая индукция при переменном. Всегда при изменении электричеством своего направления запускается механизм зарядки и разрядки, из-за чего он и пропускает переменный. Увеличение частоты приводит к снижению ёмкостного сопротивления двухполюсника.

Вам это будет интересно Световые датчики для освещения

Конденсатор в постоянной цепи

Цепи RLC

Цепи, которые содержат R, L и C, могут иметь разные варианты соединений. Цепи могут быть последовательными, разветвленными, и имеющие последовательные соединения в ветвях. Рассмотрим простые варианты. RLC последовательно.

В некоторых случаях цепи RL (моторы, трансформаторы и т. п.) имеют слишком маленький Cos φ. То есть в них слишком сильно влияние индуктивной составляющей. В такие цепи специально включают компенсационные конденсаторы, которые уменьшают фазовый сдвиг, Это разгружает источники электроэнергии от избыточной реактивной нагрузки, и обеспечивает значительную экономию электроэнергии.

Мощность в цепи с емкостью

Произведение тока и напряжения для емкости дает синусоиду, которая состоит из положительных и отрицательных полуволн, значит, средняя за период мощность равна 0.

Физический смысл состоит в том, что емкость за пол периода получает энергию, а затем пол периода возвращает ее в источник. Энергия накапливается в электрическом поле емкости, а затем возвращается в источник.  Частота синусоиды мощности вдвое больше частоты тока и напряжения.

Таким образом, на емкости не получается выделение тепла и никакой полезной мощности получить нельзя. Поэтому мощность, которая получается на емкости, называется реактивной и обозначается буквой – Qc.