Тонкий провод
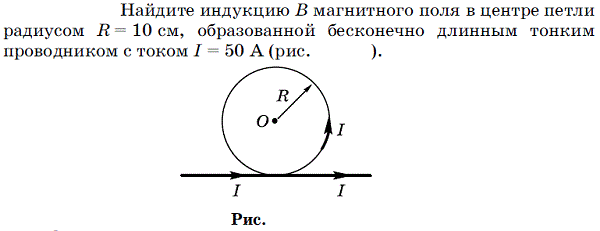
Тонкий провод изогнут в виде правильного шестиугольника. Сторона шестиугольника а-10 см. Определить магнитную индукцию В в центре шестиугольника, если по проводу течет ток / 25 А.
| Прокладка жгута с. |
Тонкие провода, покрытые эмалью, в шелковой оболочке ( ЛЭШО, ЛЭШД) освобождают от изоляции следующим образом. С конца провода снимают шелковую оболочку, а покрытые эмалью тонкие жилы провода нагревают в течение 4 – – 6 сек. В результате эмаль растрескивается и осыпается с каждой проволочки. Остатки эмали удаляют шлифовальной шкуркой.
| Схема получения полиуретанового лака.| Зависимость времени облуживания эмальпроводов от температуры. |
Тонкие провода ( диаметром до 0 15мм) могут припаиваться с помощью паяльника без зачистки изоляции и предварительного покрытия конца провода оловом.
Тонкие провода ( диаметром до 0 15 мм) можно припаивать паяльником, не зачищая изоляцию и не покрывая предварительно конец оловом. Полиуретановые эмалированные провода более нагревостойки, чем провода, эмалированные поливинилацеталевыми лаками, но уступают в этом отношении проводам с полиэфирной изоляцией. По сопротивлению изоляции в условиях повышенной влажности они превосходят провода, эмалированные лаком винифлекс.
| Зависимость времени облужи.| Зависимость термопластичности эмалевых пленок от. |
Тонкие провода ( диаметром до 0 15 мм) можно припаять паяльником, не зачищая изоляцию и не покрывая предварительно конец провода оловом. Это свойство проводов с полиуретано-вои изоляцией выгодно используют в монтаже электронной электро – и радиотехнической аппаратуры, когда приходится присоединять большое число тонких проводов к различным токо-проводящим частям схем. По сопротивлению изоляции в условиях повышенной влажности они превосходят эмальпровода на полиамидноре-зольном лаке и лаке винифлекс.
Такие тонкие провода быстро перегорали и разрушались.
Прямолинейный бесконечно длинный тонкий провод с током i 200 А подвешен на высоте h 4 5 м над плоской поверхностью идеально намагниченного тела.
Прямолинейный бесконечно длинный тонкий провод с током i 100 А протянут внутри прямого двугранного угла параллельно его сторонам, образованным веществом, магнитная проницаемость которого ц оо. Как изменится сила взаимодействия, если вещество является идеальным диамагнетиком.
Прямолинейные весьма длинные тонкие провода, образуя обмотку, уложены вплотную на поверхности немагнитного ротора радиусом R. Ток проводов распределен по закону i – I, cos а, где а – угловая координата точек поверхности ротора.
Прямолинейный бесконечно длинный тонкий провод изогнут и образует в точке А прямой угол.
Виток тонкого провода, имеющий форму квадрата, обладает индуктивностью L.
| Различные способы разделки концов провода у катушки ( А, С и Е. Устройство ответвлений от секций катушки ( А, В и D. |
Био–Савара–Лапласа
3.4.1. Индукция магнитного поля отрезка
прямолинейного проводника с током
Для
всех бесконечно малых элементов dl отрезка векторы dl
и r лежат в плоскости листа. Поэтому векторы dB,
созданные в выбранной нами точке различными элементами проводника направлены
одинаково – перпендикулярно плоскости листа. Следовательно, сложение векторов dB
можно заменить сложением их модулей dB.
Из рисунка видно, что r = b/sina (b – расстояние от проводника до инте-ресующей нас точки), и
.
Тогда индукция, созданная
элементом проводника dl, равна
.
Индукция магнитного поля, созданного
всем проводником, может быть найдена как интеграл от dB в пределах от
a1 до + a2:
Иногда удобнее воспользоваться другим
выражением:
(обратите внимание на рисунок, показывающий углы q1 и q2). Обратите также внимание на то, что
если точка расположена так, как показано на следующем рисунке, то q2 меняет знак и формула для расчёта магнитного поля
прямолинейного отрезка записывается следующим образом:
Обратите также внимание на то, что
если точка расположена так, как показано на следующем рисунке, то q2 меняет знак и формула для расчёта магнитного поля
прямолинейного отрезка записывается следующим образом:
.
прямолинейного
проводника с током
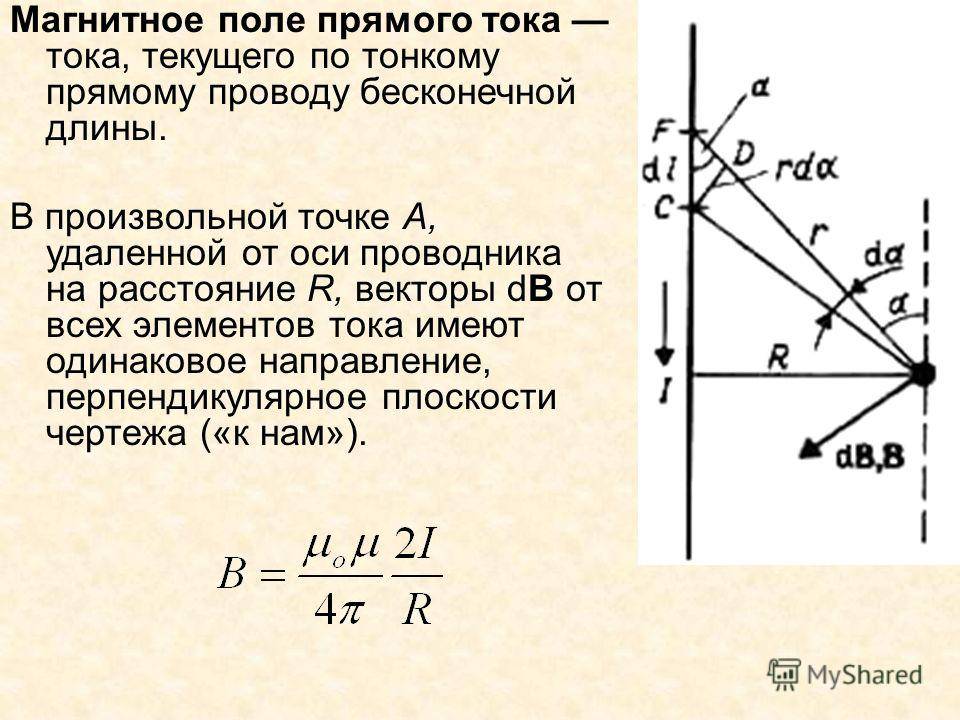
Если длина прямого проводника бесконечно
велика, то a1 = 0, а a2 = p.
В этом случае индукция магнитного
поля, созданного проводником, будет равна
.
Таким образом,
индукция магнитного поля, созданного бесконечно длинным проводником прямо
пропорциональна току в проводнике и обратно пропорциональна расстоянию от
проводника до интересующей нас точки.
Дополнительно рассмотрим
магнитное поле, созданное бесконечным проводником, который изогнут под прямым
углом.
Ограничимся получением
расчётной формулы для точки А, расположенной на продолжении одной из
половин проводника.
Участок DB в точке А
не создаёт магнитного поля, так как для него a1 и a2 равны 0.
Для участка ВС a1 = 90, a2 =
-180. Поэтому индукция, созданная этим участком, равна
.
Таким образом, индукция
магнитного поля в точке А равна половине индукции, созданной прямым
бесконечно длинным проводником с таким же током.
3.4.3. Индукция магнитного поля в центре квадрата
Рассмотрим квадрат со стороной а, в котором течёт ток I.
Все стороны
квадрата создают в его центре одинаковое магнитное поле. Поэтому если индукция,
созданная одной стороной, равна В, то магнитная индукция, созданная
всеми сторонами, равна 4В.
В рассматриваемом случае a1 = 45, а a2 =
135 (см. рисунок).
Индукция магнитного поля,
созданного одной стороной, равна:
.
Соответственно индукция магнитного
поля, созданного всеми сторонами, равна
.
В показанном на рисунке случае
индукция магнитного поля направлена перпендикулярно плоскости квадрата на нас.
3.4.4. Расчёт магнитного поля замкнутого кругового
тока
(витка
с током).
Пусть радиус витка равен R, а
ток в нём – I.
Вначале рассмотрим расчёт поля в
центре витка.
Каждый элемент тока будет создавать
индукцию, направленную вдоль оси витка. Поэтому, как и в предыдущем случае, сложение
dB алгебраическое и
,
(в каждой точке a = 90)
.
Поле на
оси витка на расстоянии b от центра витка рассчитывается несколько
сложнее. В этом случае векторы dB не параллельны друг
другу.
При суммировании составляющие
векторов dB, перпендикулярные оси, уничтожаются, а параллельные
оси – складываются.
Из рисунка видно, что
;
.
Проинтегрировав это выражение по всему
контуру, получаем
.