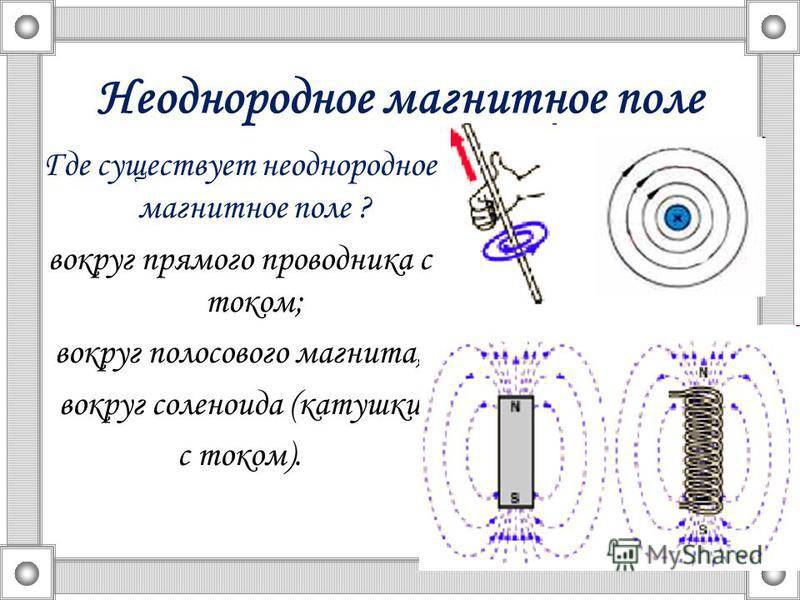
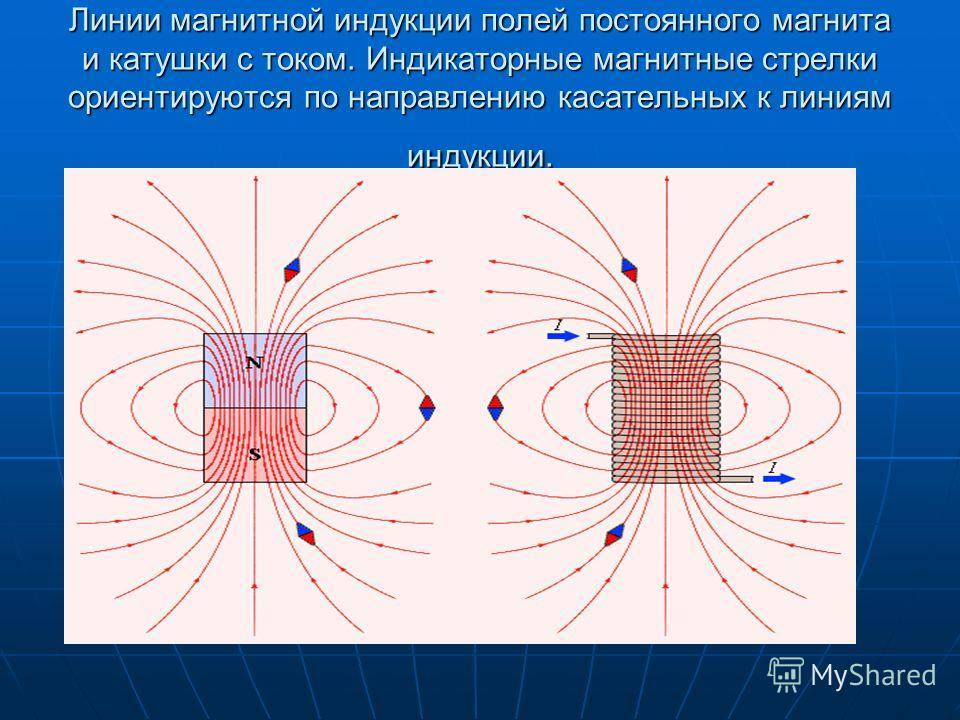
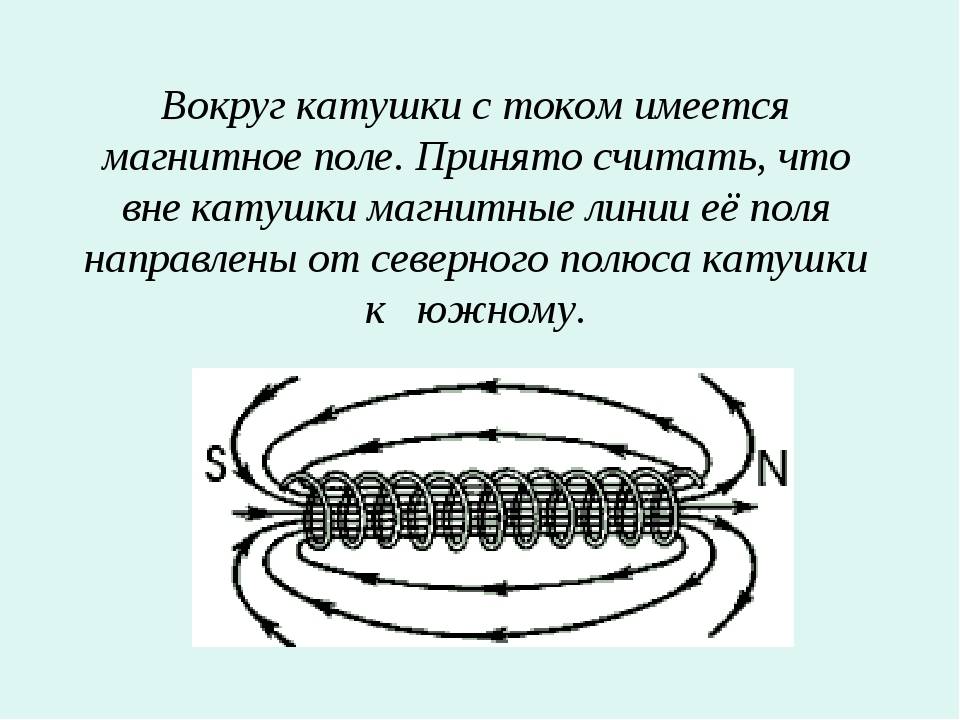
Катушка индуктивности в цепи переменного тока.
Рассмотрим цепь, в которой на катушку индуктивности подается переменный ток:

И теперь посмотрим на зависимости тока и ЭДС самоиндукции от времени, а затем уже разберемся, почему они выглядят именно так:
Как мы уже выяснили ЭДС самоиндукции у нас прямо пропорциональна и противоположна по знаку скорости изменения тока:
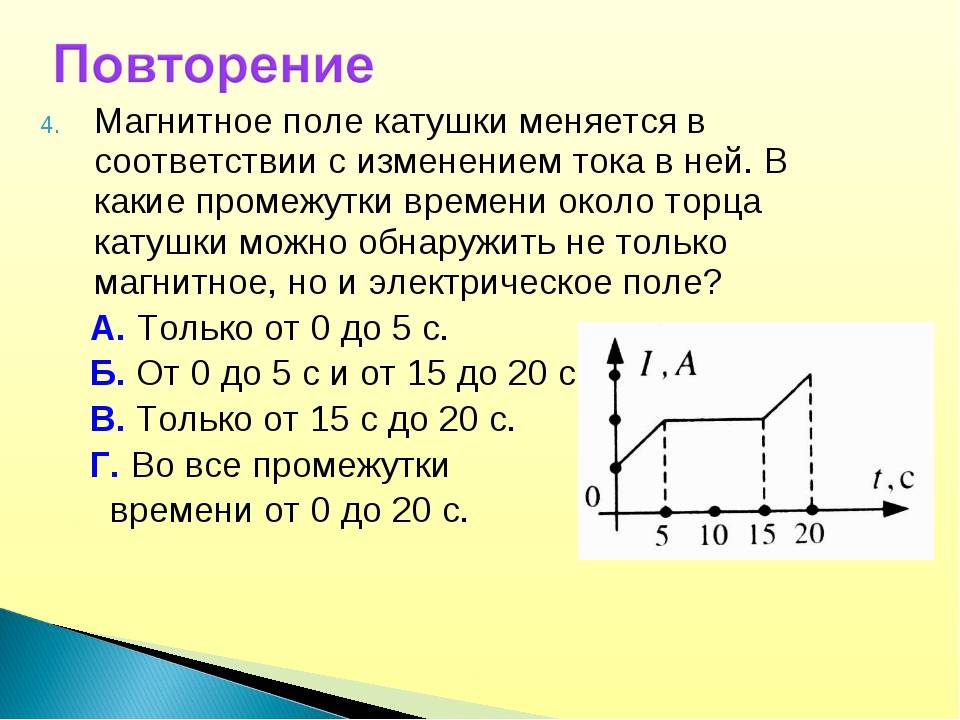
\varepsilon_L = -L\medspace\frac{dI}{dt}Собственно, график нам и демонстрирует эту зависимость. Смотрите сами – между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течение какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения. Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения.
Аналогично между точками 2 и 3 – ток уменьшается – скорость изменения тока отрицательная и увеличивается – ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика – там все процессы протекают по такому же принципу.
Кроме того, на графике можно заметить очень важный момент – при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2: \varepsilon < 0, i > 0, участок 3-4: \varepsilon > 0, i < 0). Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены “навстречу” току источника).
А на участках 2-3 и 4-5 все наоборот – ток убывает, а ЭДС препятствует убыванию тока (поскольку индукционные токи будут направлены в ту же сторону, что и ток источника и будут частично компенсировать уменьшение тока).
И в итоге мы приходим к очень интересному факту – катушка индуктивности оказывает сопротивление переменному току, протекающему по цепи. А значит она имеет сопротивление, которое называется индуктивным или реактивным, и вычисляется следующим образом:
X_L = w\medspace L
Где w – угловая частота: w = 2 \pi f. f – это частота переменного тока. Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. А если ток постоянный (f = 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.
Давайте вернемся к нашим графикам, которые мы построили для случая использования катушки индуктивности в цепи переменного тока. Мы определили ЭДС самоиндукции катушки, но каким же будет напряжение u? Здесь все просто, по 2-му закону Кирхгофа:
u + \varepsilon_L = 0
А следовательно:
u = - \varepsilon_L
Построим на одном графике зависимости тока и напряжения в цепи от времени:
Как видите ток и напряжение сдвинуты по фазе (ссылка) друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности:
Вот и с включением катушки в цепь переменного тока мы разобрались На этом, пожалуй, закончим сегодняшнюю статью, она получилась уже довольно объемной, поэтому разговор о катушках индуктивности мы продолжим в следующий раз.
«Электромагнитная индукция»
Электромагнитная индукция — это явление, которое заключается в возникновении электрического тока в замкнутом проводнике в результате изменения магнитного поля, в котором он находится. Это явление открыл английский физик М. Фарадей в 1831 г. Суть его можно пояснить несколькими простыми опытами.
Описанный в опытах Фарадея принцип получения переменного тока используется в индукционных генераторах, вырабатывающих электрическую энергию на тепловых или гидроэлектростанциях. Сопротивление вращению ротора генератора, возникающее при взаимодействии индукционного тока с магнитным полем, преодолевается за счет работы паровой или гидротурбины, вращающей ротор. Такие генераторы преобразуют механическую энергию в энергию электрического тока.
Вихревые токи, или токи Фуко
Если массивный проводник поместить в переменное магнитное поле, то в этом проводнике благодаря явлению электромагнитной индукции возникают вихревые индукционные токи, называемые токами Фуко.
Вихревые токи возникают также при движении массивного проводника в постоянном, но неоднородном в пространстве магнитном поле. Токи Фуко имеют такое направление, что действующая на них в магнитном поле сила тормозит движение проводника. Маятник в виде сплошной металлической пластинки из немагнитного материала, совершающий колебания между полюсами электромагнита, резко останавливается при включении магнитного поля.
Во многих случаях нагревание, вызываемое токами Фуко, оказывается вредным, и с ним приходится бороться. Сердечники трансформаторов, роторы электродвигателей набирают из отдельных железных пластин, разделенных слоями изолятора, препятствующего развитию больших индукционных токов, а сами пластины изготовляют из сплавов, имеющих высокое удельное сопротивление.
Электромагнитное поле
Электрическое поле, созданное неподвижными зарядами, является статическим и действует на заряды. Постоянный ток вызывает появление постоянного во времени магнитного поля, действующего на движущиеся заряды и токи. Электрическое и магнитное поля существуют в этом случае независимо друг от друга.
Явление электромагнитной индукции демонстрирует взаимодействие этих полей, наблюдаемое в веществах, в которых есть свободные заряды, т. е. в проводниках. Переменное магнитное поле создает переменное электрическое поле, которое, действуя на свободные заряды, создает электрический ток. Этот ток, будучи переменным, в свою очередь порождает переменное магнитное поле, создающее электрическое поле в том же проводнике, и т. д.
Совокупность переменного электрического и переменного магнитного полей, порождающих друг друга, называется электромагнитным полем. Оно может существовать и в среде, где нет свободных зарядов, и распространяется в пространстве в виде электромагнитной волны.
Классическая электродинамика — одно из высших достижений человеческого разума. Она оказала огромное влияние на последующее развитие человеческой цивилизации, предсказав существование электромагнитных волн. Это привело в дальнейшем к созданию радио, телевидения, телекоммуникационных систем, спутниковых средств навигации, а также компьютеров, промышленных и бытовых роботов и прочих атрибутов современной жизни.
Краеугольным камнем теории Максвелла явилось утверждение, что источником магнитного поля может служить одно только переменное электрическое поле, подобно тому, как источником электрического поля, создающим в проводнике индукционный ток, служит переменное магнитное поле. Наличие проводника при этом не обязательно — электрическое поле возникает и в пустом пространстве. Линии переменного электрического поля, аналогично линиям магнитного поля, замкнуты. Электрическое и магнитное поля электромагнитной волны равноправны.
Электромагнитная индукция в схемах и таблицах
(Явление электромагнитной индукции, опыты Фарадея, правило Ленца, закон электромагнитной индукции, вихревое электрическое поле, самоиндукция, индуктивность, энергия магнитного поля тока)
Дополнительные материалы по теме:
Конспект урока по физике в 11 классе «Электромагнитная индукция».
Следующая тема: «».
Электромагнитная индукция в движущемся проводнике
Эксперименты показывают, что ЭДС индукции возникает в любом отрезке проводника, движущемся в магнитном поле и пересекающем линии магнитной индукции. ЭДС индукции в таком «микрогенераторе» можно рассчитать с помощью схемы, представленной на Рис.1. По параллельным металлическим «рельсам», замкнутым с одной стороны проводящей перемычкой AB, в однородном поле с магнитной индукцией B с постоянной скоростью v скользит проводящий «мостик» CD длиной l . За время dt магнитный поток, пронизывающий контур ABCD, возрастает на величину dФ = Bvl·dt, откуда
Согласно основному закону электромагнитной индукции ЭДС, индуктируемая в контуре, определяется соотношением
Так как все элементы контура, кроме «мостика», неподвижны относительно магнитного поля, то (2) — это и есть ЭДС, возникающая в движущемся проводнике.
Эта же ЭДС возникает и в незамкнутом проводящем отрезке, движущемся в магнитном поле (Рис. 2). Считается, что при перемещении проводящего отрезка в магнитном поле силой, «разделяющей» заряды q в проводнике и создающей на концах такого «микрогенератора» индукционную ЭДС, является магнитная составляющая силы Лоренца:
Если скорость движения проводника постоянна, то и ЭДС индукции остается постоянной. В момент остановки заряды в проводнике под действием кулоновских сил «схлопываются» и микрогенератор практически мгновенно разряжается.
ЭДС в таком индукционном микрогенераторе возникает вследствие того, что проводник пересекает линии магнитного поля с некоторой скоростью v. Назовем (для краткости) такой способ генерации ЭДС электромагнитной индукции «способом пересечения». Процесс электромагнитной индукции «с пересечением» можно схематически представить так:
пересечение → возникновение силы Лоренца → перемещение зарядов → образование ЭДС
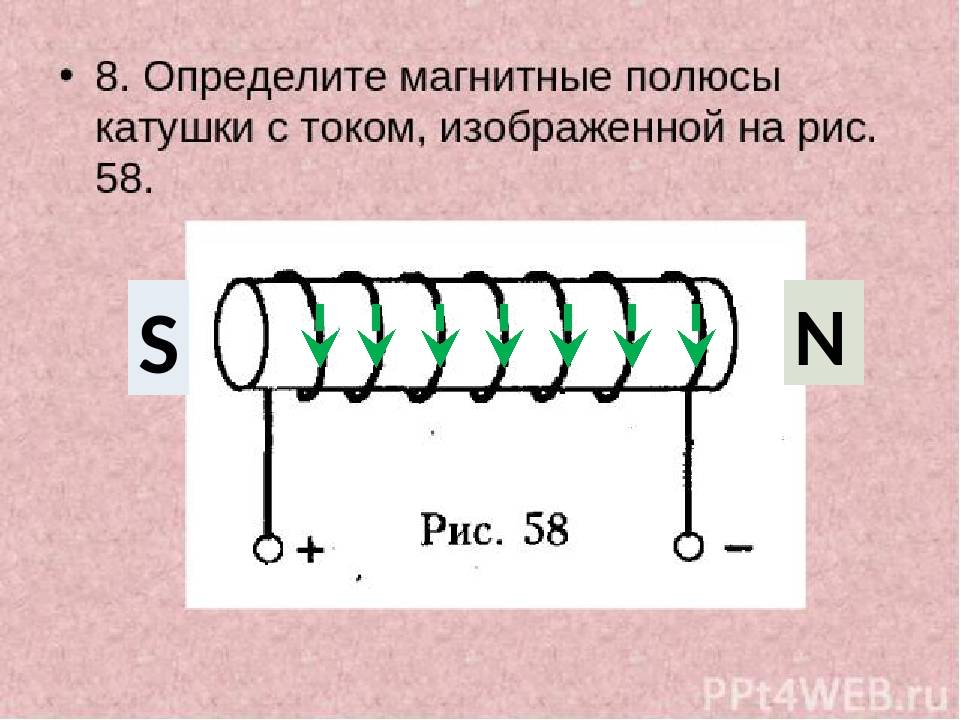
Как определить направление электрического тока в катушке
Вопрос по физике:
Укажите направление электрического тока в катушке( c объяснением)

Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Магнитный поток
Магнитным потоком через площадь \( S \) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции \( B \) , площади поверхности \( S \) , пронизываемой данным потоком, и косинуса угла \( \alpha \) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – \( \Phi \) , единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла \( \alpha \) магнитный поток может быть положительным ( \( \alpha \) \( \alpha \) > 90°). Если \( \alpha \) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Магнитопроводы для катушек
Важным параметром, характеризующим качество катушек, является добротность, численно равная отношению ее индуктивного сопротивления переменному току данной частоты к сопротивлению постоянному току. Чтобы увеличить добротность, пользуются разными конструктивными приемами, но наибольший эффект дает введение в катушку магнитопровода (сердечника) из специального магнитного материала. При внесении магнитопровода в катушку силовые линии магнитного поля концентрируются в магнитопроводе, так как его сопротивление магнитному потоку значительно меньше, чем воздуха.

Маркировка катушек.
В результате магнитный поток, а следовательно, и индуктивность катушки увеличиваются в несколько раз, что позволяет уменьшить число витков, а значит, и сопротивление катушки постоянному току. Кроме того, используя магнитолроводы, удается значительно уменьшить размеры катушек и очень простым способом (перемещением магнитопровода) осуществить регулировку их индуктивности. Поскольку катушки с магнитопроводами обычно работают в цепях переменного тока (исключение — катушки электромагнитных реле и некоторые другие), применять оплошные магнитопроводы из обычных магнитных материалов нельзя.
Будет интересно Дроссели в электрике: что это и где используются?
Под действием переменного магнитного поля в сплошном магнитопроводе, который можно рассматривать как множество короткозамкнутых витков, возникают так называемые вихревые токи, которые нагревают магнитапровол, бесполезно потребляя часть энергии магнитного поля. Чтобы уменьшить эти потери, магнитопроводы катушек, работающих в диапазоне звуковых частот, набирают из отдельных тонких изолированных пластин, изготовленных из специальных электромеханических сталей или пермаллоя. В области радиочастот стальные магнитопроводы, даже набранные из очень тонких пластин, неприменимы, так как потери на вихревые тоКи в них недопустимо велики. Магнитопроводы для катушек, предназначенных для работы на радиочастотах, изготовляют из специальных материалов: маг-нитодиэлектриков и ферритов.
В магнитодиэлектриках мельчайшие частички вещества, содержащего в своем составе железо, равномерно распределены в массе какого-либо диэлектрика (бакелита, стирола, амино-пласта). Наиболее широко применяют магнитопроводы из альсифера (сплав алюминия, кремния и железа) и карбонильного железа.
Общие сведения
Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.
Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.
Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.
Среди основных свойств индуктивности выделяются:
- Величина параметра никогда не может быть меньше нуля.
- Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.
Противостояние Тесла и Эйнштейна
Долгое время теория эфира имела превалирующее значение в физике. Однако ни разу ни один ученый не смог придумать математическую модель, описывающую поведение этой среды. Тесло умер слишком рано и не успел доказать или опровергнуть свою теорию, задумка с индукционной катушкой так же не была доведена до конца.
После на научном горизонте зажегся огонь другого гения. Альберт Эйнштейн получил Нобелевскую премию за изучение преломления световых лучей, а не за теорию относительности. Но именно вторая отлично описывала все, уже имеющиеся теории. Математическая модель, предложенная гением объясняла сам принцип распространения электромагнитных волн, тогда как философские рассуждения об эфире не имели широкого научного подтверждения.
Так идея гения физики канула в небытие, а принцип работы индуктивной катушки до сих пор не изучен до конца.
Катушка индуктивности в цепи переменного тока
- Подробности
- Просмотров: 574
«Физика – 11 класс»
Индуктивность в цепи влияет на силу переменного тока.
Есть цепь из катушки с большой индуктивностью и электрической лампы накаливания.
При подключении с помощью переключателя цепи к источнику постоянного напряжения или к источнику переменного напряжения постоянное напряжение и действующее значение переменного напряжения будут равны.
Однако лампа светится ярче при постоянном напряжении.
Значит действующее значение силы переменного тока в цепи меньше силы постоянного тока.
Это объясняется явлением самоиндукции.
При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно.
Возникающее при этом вихревое электрическое поле тормозит движение электронов.
По прошествии некоторого времени сила тока достигает наибольшего (установившегося) значения, соответствующего данному постоянному напряжению.
Если напряжение быстро меняется, то сила тока не будет успевать достигнуть тех значений, которые она приобрела бы с течением времени при постоянном напряжении.
Максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения.
Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна быть равна нулю.
Иначе сила тока, согласно закону Ома, была бы бесконечно большой.
Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля i, порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля к, создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.
Из равенства i = –к следует, что удельная работа вихревого поля (т. е. ЭДС самоиндукции) равна по модулю и противоположна по знаку удельной работе кулоновского поля.
Так как удельная работа кулоновского поля равна напряжению на концах катушки, можно записать:
ei = —u
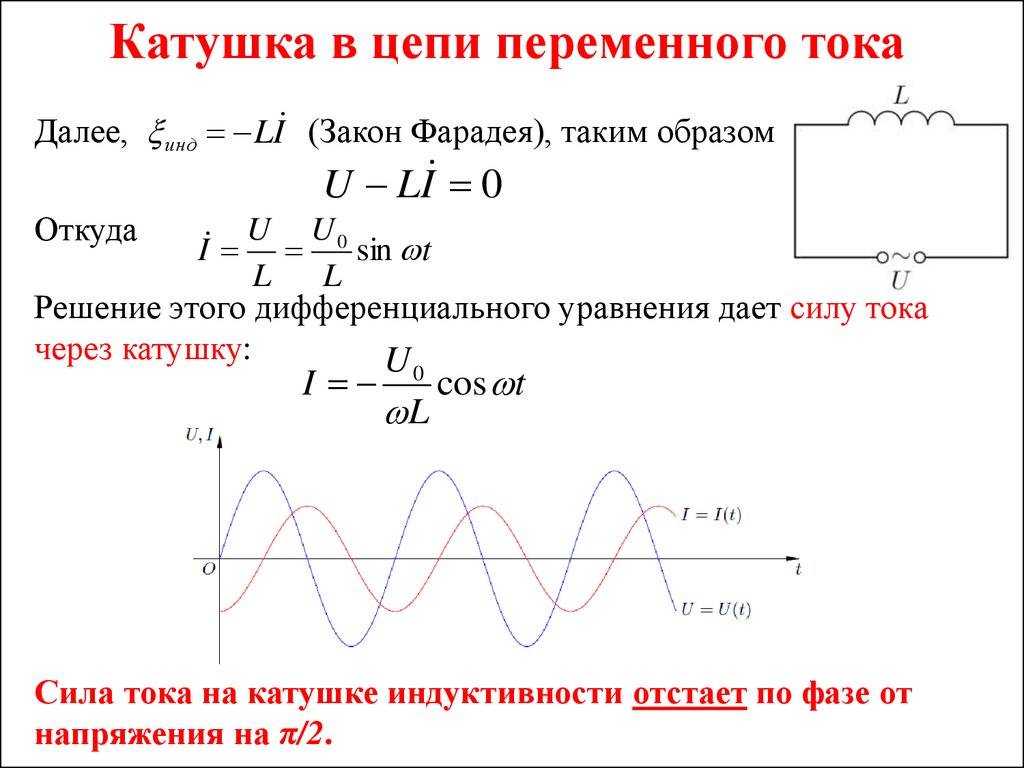
При изменении силы тока по гармоническому закону
i = Im sin ωt
ЭДС самоиндукции равна:
еi = —Li’ = —LωIm cos ωt
Так как u = —ei напряжение на концах катушки оказывается равным

гдеUm = LωIm — амплитуда напряжения.
Колебания напряжения на катушке опережают по фазе колебания силы тока на , или, что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на .
Амплитуда силы тока в катушке равна:
Если ввести обозначение
ωL = ХL
и действующие значения силы тока и напряжения, то получим:
Величину XL, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.
Действующее значение силы тока связано с действующим значением напряжения и индуктивным сопротивлением соотношением, подобным закону Ома для цепи постоянного тока.
Индуктивное сопротивление зависит от частоты ω.
Постоянный ток вообще «не замечает» индуктивности катушки.
При ω = 0 индуктивное сопротивление равно нулю (XL = 0).
Чем быстрее меняется напряжение, тем больше ЭДС самоиндукции и тем меньше амплитуда силы тока.
Итак,
Катушка индуктивности оказывает сопротивление переменному току.
Это сопротивление, называемое индуктивным, равно произведению циклической частоты на индуктивность.
Колебания силы тока в цепи с индуктивностью отстают по фазе от колебаний напряжения на .
Следующая страница «Резонанс в электрической цепи»
Назад в раздел «Физика – 11 класс, учебник Мякишев, Буховцев, Чаругин»
Электромагнитные колебания. Физика, учебник для 11 класса – Класс!ная физика
Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях —
Аналогия между механическими и электромагнитными колебаниями —
Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний —
Переменный электрический ток —
Активное сопротивление. Действующие значения силы тока и напряжения —
Конденсатор в цепи переменного тока —
Катушка индуктивности в цепи переменного тока —
Резонанс в электрической цепи —
Генератор на транзисторе. Автоколебания —
Краткие итоги главы
Как сделать катушку Теслы
На самом деле было несколько некорректно расписывать, как сделать такой прибор дома самостоятельно, так как он может быть очень опасен как для людей, так и для домашней техники. Достаточно просто знать, что это возможно и на YouTube полно роликов о том, как приобщиться к этому явлению.
Добавлю только, что для создания миниатюрной катушки достаточно обзавестись несколькими вещами, которые можно найти в гараже более-менее запасливого ”самоделкина”.

Сделанная в домашних условиях катушка Теслы может даже зажигать лампочки рядом с ней.
По сути вам понадобится только источник питания, небольшой конденсатор, маленькая катушка проводника для первичной обмотки, пара сотен метров тонкой медной эмалированной проволоки для вторичной обмотки, диэлектрическая труба для ее намотки и все.
Если вы решили сделать что-то подобное, то в каждом ролике более точно расскажут, что нужно для эксперимента. Но помните, что без специальной подготовки это может быть смертельно опасно.
Катушка индуктивности в цепи постоянного тока.
И, в первую очередь, разберемся, что происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? Однозначно нет. Ведь постоянный ток можно “включать/выключать”, и как раз в моменты переключения и происходят все ключевые процессы. Давайте рассмотрим цепь:
Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь. Что же произойдет в тот момент когда мы замкнем выключатель?
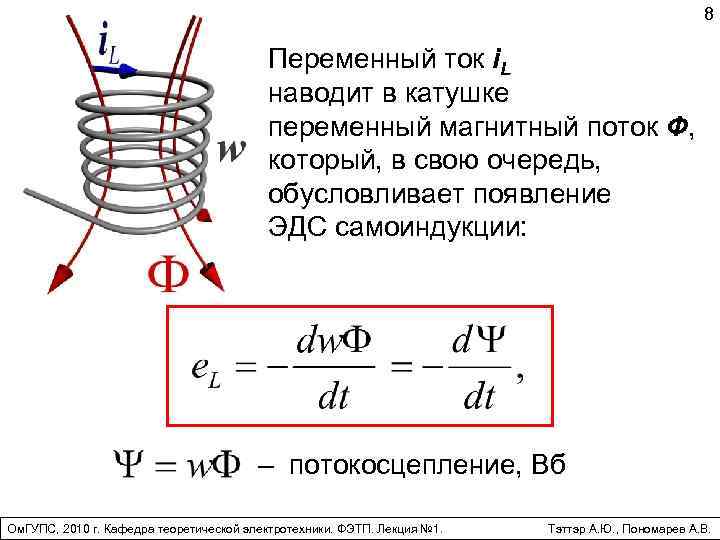
Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:
\varepsilon_s = -\frac{d\Phi}{dt}Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку I_L будет равен 0. В этот момент времени ЭДС самоиндукции максимальна.
А далее произойдет следующее – поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот, будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:
На первом графике мы видим входное напряжение цепи – изначально цепь разомкнута, но при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать.
Напряжение на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый).
Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:
После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции, в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).
Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является как раз индуктивность катушки:
\varepsilon_s = -L\medspace\frac{dI}{dt}На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим к цепям переменного тока.
Важный (!) нюанс заключается в том, что напряжение на катушке при описанных переходных процессах может достигнуть весьма значительных величин. Это, в свою очередь, легко может привести к выходу из строя тех или иных компонентов, входящих в состав цепи. Например, при управлении индуктивной нагрузкой при помощи ключа на транзисторе явление возникновения ЭДС самоиндукции с впечатляющей вероятностью приведет к выходу транзистора из строя. Для защиты от этого параллельно индуктивной нагрузке ставят защитный диод, но сегодня речь не об этом, поэтому для данного аспекта я опубликую отдельный материал с рассмотрением основных нюансов.
Реактивное сопротивление катушки индуктивности
Поскольку в первую половину периода энергия электрического тока запасается в магнитном поле катушки, а во вторую — возвращается в цепь, то в среднем работа электрического тока равна по модулю работе ЭДС самоиндукции, но имеет противоположный знак:
$$e_i =-u$$
Однако амплитудные значения напряжения и тока на катушке индуктивности достигаются неодновременно.
Мгновенное значение тока:
$$i =I_msin \omega t$$
Мгновенное значение напряжения:
$$u =L\omega I_m cos \omega t$$
Учитывая, что максимальная амплитуда напряжения $U_m$ равна $ L\omega I_m $, и приводя к синусу, получаем:
$$u =U_m sin(\omega t+{\pi \over 2})$$
Таким образом, колебания силы тока в катушке индуктивности отстают от колебаний напряжения на четверть периода
В этом важное отличие реактивного сопротивления от активного, где отставания между током и напряжения нет
 Рис. 2. Графики тока и напряжения для индуктивности.
Рис. 2. Графики тока и напряжения для индуктивности.
Амплитуда силы тока в катушке равна:
$$I_m={U_m\over \omega L}$$
Сравним эту формулу с законом Ома, который используется для определения силы тока в цепи:
$$I={U\over R}$$
Можно видеть, что эти формулы аналогичны, и величина $ \omega L$ играет роль сопротивления. То есть реактивное сопротивление катушки индуктивности (индуктивное сопротивление) равно:
$$X_L= \omega L$$
Отметим, что реактивное сопротивление катушки прямо пропорционально циклической частоте переменного тока. Чем она больше, тем больше сопротивление.
Поскольку любой проводник обладает некоторой индуктивностью, то на очень высоких частотах даже эта малая индуктивность обычных проводников достаточно сильно влияет на сигнал. Поэтому приходится применять специальные меры для ее компенсации. Например, применять вместо проводов волноводы — пустотелые металлические конструкции:
 Рис. 3. Волноводы.
Рис. 3. Волноводы.
Что мы узнали?
Катушка индуктивности в цепи переменного тока обладает реактивным сопротивлением, пропорциональным частоте. Первую половину периода она запасает энергию электрического тока в виде магнитного поля, а вторую половину периода возвращает эту энергию электрическому току. При этом колебания силы тока в катушке индуктивности отстают от колебаний напряжения на четверть периода.
/10
Вопрос 1 из 10
Виды и типы
Различают низкочастотные, высокочастотные модели. В отдельную категорию выделяют винтовые, спиральные катушки. Также существуют модификации, которые используются в радиотехнике. Они подходят для защиты конденсатора либо резонансных контуров.

Для трансформаторов годятся катушки с усилителем каскадом. В последнюю категорию выделены вариометры, основное отличие — высокая частота колебательных контуров. Дроссели могут быть одинарными либо сдвоенными. От этого зависит показатель индуктивности и питания системы.
Низкочастотные
Для включения в электрическую цепь, применяется низкочастотная катушка индуктивности. Она предназначена для подавления переменного тока. В формуле учитывается циклическая частота и показатели индуктивности. За основу в устройствах берётся сердечник, который изготавливается из стали. Он может быть с фильтрами либо без них.
Чтобы влиять на частоту, происходит игра с сопротивлением. В цепи постоянного тока напряжение должно быть неизменным. С целью понижения частоты применяются фильтры. Основная проблема — это малая ёмкость. Чтобы детально ознакомиться с дросселем, стоит подробнее узнать о резонансной частоте, которая выделяется на контуре рабочего сигнала.
Когда в цепях повышается напряжение, на каркас оказывается нагрузка. В цепи постоянного тока задействуются непрозрачные проволочные резисторы. Также для этих целей подходят однослойные катушки типа «универсал». Их особенность — использование ферритовых стержней.
Низкочастотная катушка
Высокочастотные
Устройства изготавливаются с различными типами обмотки. Речь идет о наборе преимуществ, которые спасают в той или иной ситуации. Сфера применения элементов широка, учитывается значительная частота модуляции. Таким образом удается бороться с повышенным сопротивлением металлов. У катушек имеется сердечник.
Основная задача — это модуляция частоты генератора. Она происходит за счёт усиления сигнала, и за процессом можно проследить при подключении осциллографа. Многие высокочастотные катушки не отличаются стабильной работой, поскольку применяется керамический каркас. У него малый срок годности, плюс они восприимчивы к повышенной влажности.
Интересно! Современные товары изготавливаются из алюминия и являются компактными.
Электрикам известны контурные, безконтурные модификации высокой частоты. В зависимости от намотки учитывается стабильность электрических параметров. У моделей высокой частоты могут применяться магниты и провода. Речь идет о порошковых материалах, сделанных из диэлектриков.
Процесс изготовления связан с методом холодного прессования. Индуктивные датчики отличаются по защищенности. На предприятиях элементы могут погружать в раствор либо продевать в трубку. Это делается с целью избежания коротких замыканий. Мировые производители решают проблему путем использование вторичного витка.
Высокочастотная катушка
У моделей значительное сопротивление и есть проблема с концентрацией электролита. Таким образом изменяются свойства катушки индуктивности. Проводимость раствора падает и повышается частота электромагнитного поля.


![Взаимная связь электрических и магнитных полей [1973 григорьев в.и., мякишев г.я. - силы в природе]](https://ledsshop.ru/wp-content/uploads/9/d/7/9d72109f0449b64c41aec745f054d452.jpeg)