Ток резистора сопротивление которого 8 ом равен 2 4

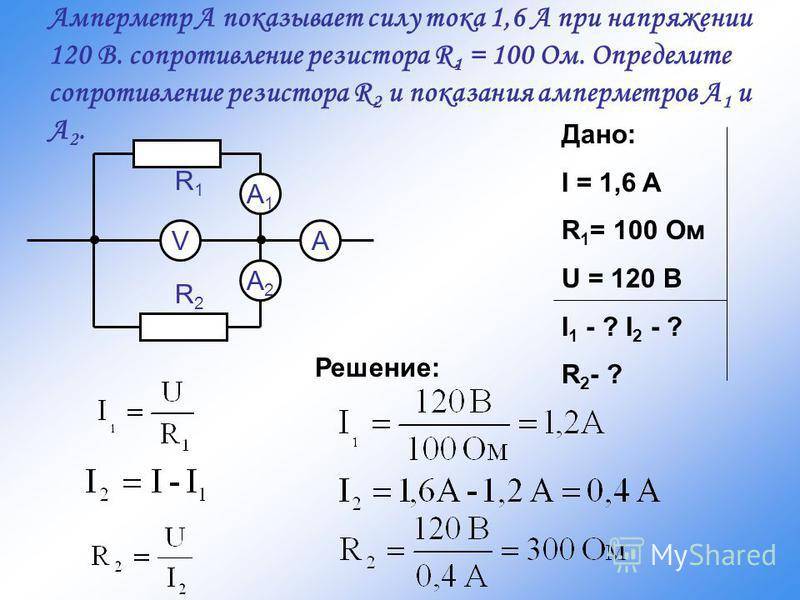
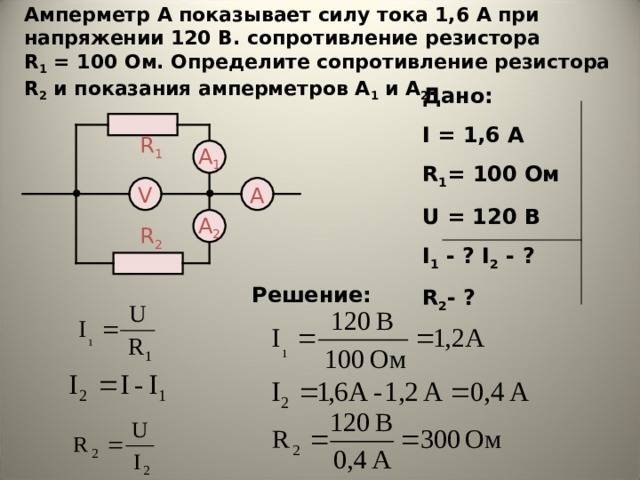
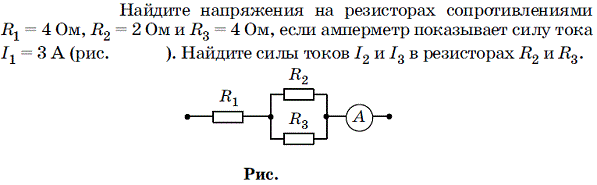
Расчет параллельного соединения резисторов

Общее сопротивление

Для лучшего понимания процессов следует подробно рассмотреть представленную ниже схему. В контрольных точках (разрывах цепей) условно показаны измерительные приборы. Аналогичным образом подключают мультиметр для уточнения результатов теоретических вычислений. Чтобы не усложнять объяснение, использован «идеальный» источник постоянного тока. Его сопротивление в расчетах не учитывается. Аналогичным образом игнорированы емкостные (индуктивные) реактивные составляющие, которые способны создать незначительные нелинейные искажения.

Электрическая схема с пояснительными формулами

В рассматриваемом примере ток (I) идет по замкнутому контуру от положительного к отрицательному электроду АКБ. На входе параллельного участка (точка «а») он разделяется на I1 (I2), проходящие через разные ветки с электрическими сопротивлениями R1 (R2), соответственно. В точке «б» происходит объединение токов.

Если присоединить клеммы мультиметра к положительной клемме аккумулятора и входной точке, а после повторить измерение на выходе, будут определены одинаковые значения. Однако в отдельных ветвях токи будут отличаться, если применены разные сопротивления (R1≠R2). Сложение показаний подтвердит равенство суммы полученным ранее результатам измерений на входе (выходе). Промежуточный вывод, подтвержденный экспериментально:

Iобщ = I1 + I2.

Далее можно проверить разницу потенциалов на клеммах источника питания (Uип), в контрольных точках (Uаб) и на отдельных резисторах (UR1 и UR2). Несложно убедиться в том, что Uип = Uаб = UR1 = UR2. Для отдельных ветвей будут действительны пропорции:

• UR1 = I1 * R1;
• UR2 = I2 * R2.

Однако с учетом результатов измерений можно приравнять обе стороны выражений:

UR1 = UR2 = I1 * R1 = I2 * R2.

Простым преобразованием получают соотношение:

I1/I2 = R2/R1.

На основе этой формулы надо сделать следующий важный вывод: токи обратно пропорциональны электрическим сопротивлениям в соответствующих ветвях параллельной цепи.

Пример с исходными данными:

• батарейка Uип = 6V;
• сопротивление параллельных резисторов: R1 = 50 Ом, R2 = 150 Ом.

Расчет:

• найти ток в первой ветке можно по формуле: I1 = Uип / R1 = 6/50 = 0,12А = 120 мА;
• аналогичным образом вычисляют: I2 = Uип / R2 = 6/150 = 0,04А = 40 мА;
• суммарное значение: Iобщ = I1 + I2 = 120 + 40 = 160 мА;
• соблюдается отмеченный выше принцип пропорциональности: I1/I2 = R2/R1 = 50/150 = 40/120 ≈ 0,333.

Следует отметить разную силу тока в отдельных ветках. Для наглядности можно вспомнить пример с аналогом из водопроводных труб. В разветвленном участке по протоку с крупным диаметром пройдет больше жидкости, по сравнению с другим за контрольный временной интервал. Аналогичным образом действует электрическое сопротивление. При увеличении номинала пассивного элемента создаются дополнительные препятствия прохождению тока.

Для расчета сложных схем используют технологию эквивалентных сопротивлений. Этим термином обозначают расчетную величину (Rэкв), которая равна сумме измеряемых параметров отдельных компонентов на определенном участке цепи. Проще всего сделать вычисления, если соединить резисторы (номиналы из примера) последовательно:

Rэкв = R1 + R2 = 50 + 150 = 200 Ом.

Ниже подробно рассмотрен вариант с параллельной схемой:

• по закону Ома для всей цепи действительно выражение: Iобщ = Uип/ Rэкв;
• в отдельных ветках: I1 = U1/ R1 (I2 = U2/ R2);
• по закону Кирхгофа для каждого провода: I = I1+ I2;
• преобразование перечисленных соотношений позволяет сделать промежуточный вывод: Uип/ Rэкв = U1/ R1 + U2/ R2;
• с учетом равенства напряжений: Uип = U1 = U2, можно переделать предыдущую формулу следующим образом: Uип/ Rэкв = Uип / R1 + Uип / R2 = Uип (1/R1 + 1/R2);
• делением на общий множитель Uип получают итоговое выражение: 1/Rэкв = 1/R1 + 1/R2.

Последняя позиция позволяет сделать несколько важных заключений:

• общая проводимость (величина, обратная электрическому сопротивлению) равна сумме проводимостей параллельных участков цепи;
• эквивалентное сопротивление можно вычислить делением единицы на проводимость;
• Rэкв при параллельном соединении всегда меньше самого меньшего из пассивных компонентов цепи.

Физические формулы и примеры вычислений

Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:

• параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
• последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.

У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.

Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:

• R1 = 1 Ом;
• R2 = 2 Ом;
• R3 = 3 Ом;
• R4 = 6 Ом;
• R5 = 9 Ом;
• R6 = 18 Ом;
• R7 = 2Ом;
• R8 = 2Ом;
• R9 = 8 Ом;
• R10 = 4 Ом.

Напряжение, поданное на схему:

U = 24 В.

Требуется рассчитать токи на всех резистивных элементах.

Исходная цепь

Для расчётов применяется закон Ома:

I = U/R, подставляя вместо R эквивалентное сопротивление.

Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте. Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения

Делают расчёты для каждого такого звена, после – всей цепи целиком

Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.

На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:

• АВ – участок, имеющий две параллельных ветви;
• ВС – отрезок, вмещающий в себя последовательное сопряжение;
• CD – отрезок схемы с расположением трёх параллельных цепочек.

Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.

Последовательно соединённые резисторы R2 и R3

Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.

Смешанное включение на участке CD

Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:

• Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
• Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
• Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.

Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.

Результат первого свёртывания

Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:

• Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
• Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
• 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.

В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.

Результат последующего свёртывания

Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:

Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.

Далее, используя закон Ома, находят ток в последнем последовательном участке:

I = U/ Rэкв. = 24/56,83 = 0,42 А.

Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:

• UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
• UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
• UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.

Следующим шагом станет определение токов на параллельных отрезках AB и CD

• I1 = UAB/R1 = 0,35/1 = 0,35 А;
• I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
• I3 = UCD/R6 = 0,17/18 = 0,009 А;
• I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
• I7 = UCD/R10 = 0,17/4 = 0,04 А.

Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.

U9 = R9*I6 = 8*0,02 = 0,16 В.

Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.

U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.

После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:

• I4 = U7,8/R7 = 1/2 = 0,5 A;
• I5 = U7,8/R8 = 1/2 = 0,5 A.

Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.

От чего зависит сопротивление резистора

Температура и последовательность включения – два главных фактора, которые определяют сопротивление в цепи. Но помимо этих показателей есть и допуски. Как же измерять? В большинстве электрических или электронных цепей большой 20% -ный допуск на один и тот же резистор, как правило, не является проблемой, но если для высокоточных цепей, таких как фильтры, генераторы или усилители и т. д., требуются резисторы с малым допуском, то необходимо использовать резистор с правильным допуском. Так как резистор с допуском 20% обычно не может использоваться для замены типа допуска 2% или даже 1%.

Цветовой код пяти- и шестиполосного резистора чаще всего ассоциируется с высокопрецизионными типами пленок 1% и 2%, в то время как универсальные садовые разновидности 5% и 10% общего назначения обычно используют четырехполосный цветовой код резистора. Резисторы имеют различные допуски, но наиболее распространенными являются E12 и E24 .

Е12 серия поставляется в двенадцати значений сопротивления за десятилетие (А десятилетие , представляющее кратные 10, то есть 10, 100, 1000 и т.д.), в то время как Е24 серия приходит в двадцать четыре значений за десятилетие и E96 серии девяносто шесть значений за десятилетие. Серия E192 с очень высокой точностью теперь доступна с допусками до ± 0,1%, что дает массивные 192 значения отдельных резисторов за десятилетие.

Как зависит от температуры

Чем выше температура, тем выше сопротивление. Это связано с быстрой скоростью движения атомов внутри твердого тела. Обратное явление – сверхпроводимость при низких температурах. Опять же, не забываем про погрешность.

От других параметров

Если резистор подключен в сложную цепь с множеством преобразующих, защитных, трансформирующих, компрессирующих устройств, то он будет иметь другое, отличное от стандартного, сопротивление, так как часть напряжения все равно будет проходить через него в нескомпрессированном виде, что не позволит ему отработать как следует. Чтобы более точно узнать удельный ток и сопротивление, показатель, полученный в расчетах, нужно уменьшить или увеличить на заданную величину.

Единица измерения сопротивления резистора

В Международной системе единиц (СИ) сопротивление измеряется в омах – единице измерения, названной так в честь физика Георга Ома, который также открыл знаменитый закон для электрической цепи. Международное обозначение выглядит так: Ω. Физический смысл этой единицы заключается в следующем:

Сопротивление проводника равно 1 Ом при силе тока, равной 1 А, и напряжении на концах проводников, равном 1 В.

Оно может быть измерено с помощью прибора, называющегося омметр.

Существует большое разнообразие резисторов с широкой линейкой стандартных величин сопротивления. Рассмотрим соотношение этих номиналов и различные приставки, использующиеся для их обозначения.

Приставка кило- (килоом):

1 КОм равен 1000 Ом

Приставка мега- (мегаом):

1 МОм соответствует 1000 КОм или 1 000 000 Ом

Часто показатели резисторов наносятся непосредственно на их корпус. Это очень удобно. Рассмотрим обозначение их номиналов более подробно.

Номинал резистора — это то же самое, что его сопротивление. Раньше резисторы были достаточно крупными, поэтому все значения прописывались целиком на их корпусах с использованием обычных букв. Помимо сопротивления на резисторе могли указать ещё и класс точности или мощность рассеивания.

Сопротивление – основная характеристика резистора. О том, что оно из себя представляет и как рассчитывается, было рассказано выше, поэтому сейчас подробнее остановимся на особенностях их обозначений.

Для простановки значения, не привышающего 1КОм после цифры, обозначающей величину сопротивления, ставится R (или величина указывается совсем без буквы). На резисторах, выпускавшихся давно, можно встретить слово Ом. Позже принятая маркировка изменилась, теперь она используется в формате:

целая величина — R — дробный остаток

Примеры обозначений:

300 = 300 Ом
200 R = 200 Ом

Современные обозначения выглядят так:

4R02 = 4,02 Ом
2R2 = 2,2 Ом

Если значение меньше 1 ома, то ноль в начале обозначения опускают:

0R5 = R5 = 0,5 Ом

Если сопротивление больше тысячи ом, то применяются специальные приставки (мега-, кило-) для упрощения написания. Очень большие значения этой величины почти не встречаются, поэтому необходимость в префиксах Тера- и Гига- возникает крайне редко. Примеры обозначений:

K200 = 200 Ом
2К0 = 2 КОм = 2000 Ом
M200 = 0,2 МОм = 200 KОм = 100 000 Ом
3М0 = 3 МОм = 3 000 КОм = 3 000 000 Ом

Дополнительно можно рассмотреть следующую характеристику — удельное сопротивление.

Бывает, что возникает необходимость также рассчитать удельное сопротивление. Оно измеряется величиной Ом*м.

Для однородного проводника вычисляемое удельное сопротивление находится так:

R = (ρ*l) / S, где

l — длина отрезка проводника (м),

S — площадь сечения проводникового элемента (м2)

Подробнее о буквенной маркировке резисторов читайте здесь.

4 вариант

1. Переведите в амперы силу тока, равную 700 мА и 0,25 кА.

1) 7 А и 250 А
2) 0,7 А и 25 А
3) 7 А и 25 А
4) 0,7 А и 250 А

2. Какой амперметр измерит силу тока в верхней (на схеме) лампе?

1) №1
2) №2
3) Любой из них
4) Ни один из этих приборов

3. При прохождении по участку цепи заряда 100 Кл электриче­ский ток произвел работу, равную 12 кДж. Каково напряже­ние на этом участке цепи?

1) 120 В
2) 12 В
3) 1,2 В
4) 0,12 В

4. На каком приборе измеряет напряжение вольтметр, включен­ный так, как показано на схеме?

1) На звонке
2) На лампе
3) На реостате

5. В чем главная причина того, что проводники оказывают со­противление электрическому току?

1) Постоянное хаотическое движение электронов
2) Столкновение упорядоченно движущихся электронов с ио­нами кристаллической решетки
3) Взаимодействие электронов с ионами решетки

6. Пользуясь законом Ома, получите формулу для расчета сопро­тивления проводника.

1) R = U/I
2) I = q/t
3) P = A/t

7. При какой силе тока напряжение на концах проводника со­противлением 125 Ом будет равно 1,5 кВ?

1) 1,2 А
2) 12 А
3) ≈ 83 А
4) ≈ 8,3 А

8. Сила тока в реостате 0,8 А, его сопротивление 100 Ом. Определите напряжение на его клеммах.

1) 125 В
2) 12,5 В
3) 80 В
4) 800 В

9. От каких физических величин зависит сопротивление прово­дника?

1) От его длины (l)
2) От площади его поперечного сечения (S)
3) От удельного сопротивления (ρ)
4) От всех этих трех величин

10. Какое вещество — с малым или большим удельным сопротив­лением — может служить хорошим проводником электриче­ства?

1) С малым
2) С большим
3) Однозначного ответа нет

11. Железный провод длиной 6 м и площадью поперечного сече­ния 0,3 мм2 включен в цепь. Какое сопротивление он оказыва­ет электрическому току?

1) 36 Ом
2) 18 Ом
3) 2 Ом
4) 20 Ом

12. У реостата, показанного на рисунке, когда он был включен в цепь, передвинули ползунок вправо. Как изменилась при этом сила тока?

1) Уменьшилась
2) Увеличилась
3) Не изменилась

13. Сила тока в лампе №1 равна 5 А. Какова сила тока в такой же лампе №2 и какую силу тока покажет амперметр?

1) 2,5 А; 5 А
2) 5 А ; 10 A
3) 2,5 А; 7,5 А
4) 5 А; 7,5 А

14. В цепи с последовательным соединением потребителей тока (двух ламп и резистора, обладающих одинаковыми сопротив­лениями) сила тока равна 0,4 А, напряжение на резисторе 20 В. Определите общее сопротивление цепи и напряжение на по­люсах источника тока.

1) 150 Ом; 40 В
2) 50 Ом; 60 В
3) 150 Ом; 20 В
4) 150 Ом; 60 В

15. В каких единицах должны быть выражены величины при рас­чете работы электрического тока по формуле А = IUt?

1) В амперах, вольтах и секундах
2) В амперах, вольтах, минутах
3) В вольтах, омах, часах
4) В кулонах, вольтах, секундах

16. Если известна мощность электрического тока, то как найти силу тока в цепи?

1) I = U/R
2) I = P/U
3) I = q/t
4) I = A/(Ut)

17. Электролампа, сопротивление нити накала которой 20 Ом, включена в сеть с напряжением 220 В. Какова мощность тока? Какую работу он произведет за 5 мин свечения лампы?

1) 4,4 кВт; 1320 кДж
2) 4,4 кВт; 22 кДж
3) 2,42 кВт; 22 кДж
4) 2,42 кВт; 726 кДж

18. Какая из формул выражает закон Джоуля — Ленца?

1) Q = cm(t₂ — t₁)
2) F = k(l₂ — l₁)
3) Q = I2Rt

19. Как и во сколько раз надо изменить силу тока в цепи, чтобы при уменьшении ее сопротивления в 4 раза выделение тепло­ты в ней осталось прежним?

1) Уменьшить в 2 раза
2) Увеличить в 4 раза
3) Уменьшить в 4 раза
4) Увеличить в 2 раза

20. Проводник обладает сопротивлением 80 Ом. Какое количество теплоты выделится в нем за 10 с при силе тока 0,3 А?

1) 7,2 Дж
2) 72 Дж
3) 720 Дж

Ответы на тест по физике Законы электрического тока1 вариант
1-2
2-1
3-4
4-2
5-3
6-1
7-4
8-2
9-2
10-3
11-4
12-2
13-3
14-1
15-3
16-2
17-4
18-3
19-1
20-32 вариант
1-2
2-4
3-4
4-2
5-1
6-3
7-2
8-2
9-1
10-3
11-4
12-1
13-4
14-2
15-3
16-3
17-1
18-4
19-2
20-23 вариант
1-3
2-3
3-2
4-1
5-3
6-4
7-1
8-4
9-3
10-2
11-3
12-1
13-4
14-1
15-3
16-2
17-1
18-2
19-3
20-24 вариант
1-4
2-4
3-1
4-2
5-3
6-1
7-2
8-3
9-4
10-1
11-3
12-2
13-2
14-4
15-1
16-2
17-4
18-3
19-4
20-2

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Пример  №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление  R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

• Таким образом, протекающий общий ток в цепи  можно определить как:
• I = I1 + I2
• Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
• Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
• Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
• Таким образом, общий ток будет равен:
• I = 0,545 мА + 0,255 мА = 0,8 мА
• Это также можно проверить, используя закон Ома:
• I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
• где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
• И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Пускорегулирующие реостаты

Реостаты, имеющие ступенчатое сделаны из резисторов и переключающего устройства, состоящего, в свою очередь, из неподвижных контактов, одного скользящего контакта. Здесь же имеется привод.

Пускорегулирующие реостаты имеют полюсы якоря, который присоединяется к неподвижным контактам. Подвижный контакт замыкает и размыкает ступени сопротивления, а также и другие цепи, которые управляются данным реостатом. Привод в реостате может быть двигательным или ручным. Это что такое? Реостат такого типа широко распространен. Но недостатки у такой конструкции все же имеются. Это большое количество проводов для монтажа и деталей для крепежа. Особенно много их в реостатах возбуждения с большим числом ступеней.

Реостаты, наполненные маслом, состоят из переключающего устройства и пакетов резисторов, которые встроены в бак и погружены в масло. Пакеты состоят из элементов, выполненных из Они прикрепляются к крышке бака.

Устройство переключения имеет вид барабана и является осью с прикрепленными к ней частями цилиндрической поверхности, которые соединены, согласно схеме. Неподвижные контакты, которые соединены с элементами резистора, крепятся на неподвижную рейку. Когда ось барабана поворачивается приводом либо маховиком, эти части перемыкают неподвижные контакты, являясь контактами подвижными. Этим изменяется сопротивление в цепи.

Вышесказанное полностью проясняет вопрос, что такое реостат. Как видно, это очень важный элемент, который широко применяется в различных

§ 1 Реостат: принцип работы и устройство

Важным элементом управления сопротивлением электрической цепи является реостат. В нем используется проводник из известного материала с определенной длинной, позволяющей рассчитать его сопротивление. Принцип работы заключается в изменении сопротивления, а значит, появляется возможность регулировать силу тока и напряжение в электрических цепях. Рассмотрим устройство реостата.

На рисунке 1 представлен реостат, состоящий из керамической трубы (1), на которую намотан провод (2) и имеются два контакта (3а), также штанга, в конце которой расположен контакт (3б). По ней движется скользящий контакт (4), который называют «ползун».

При расположении «ползуна» посередине (рис. 2а) только половина проводника принимает участие в электрической цепи. При передвижении его дальше (рис. 2б) длина проводника возрастает, и сопротивление увеличивается, но сила тока уменьшается. Передвигаем «ползун» в противоположную сторону (рис. 2в), и сопротивление уменьшится, а сила тока в цепи возрастет.

Внутри реостат полый, так как при протекании тока происходит нагревание реостата, а полость способствует быстрому охлаждению.

§ 2 Обозначения реостата на схемах и его использование

Как известно, каждый элемент цепи обозначается символом. Обозначение реостата (рис. 3):

Красный прямоугольник — сопротивление, синий — контакт, подводящий провод, зеленый — скользящий контакт. Если ползунок передвинуть влево, сопротивление реостата уменьшается, а при движении вправо — увеличивается.

Используют еще одно обозначение реостата (рис. 4):

На схеме прямоугольник обозначает сопротивление, а стрелка — то, что его можно изменять.

В электрическую цепь реостат включают последовательно. Рассмотрим схему включения реостата (рис. 5):

Зажимы (1) и (2) подключаются к источнику тока. Второй контакт подсоединен к ползунку. Увеличивая сопротивление реостата, накал лампочки (3) начинает уменьшаться, а значит, ток в цепи тоже уменьшается. Если уменьшить сопротивление реостата лампочка будет гореть ярче.

Реостат — универсальный прибор. Его используют в бытовых приборах. Например, в телевизорах для регулирования громкости и при переключении каналов. Для безопасности используют реостаты с защитным кожухом (рис. 6).

Список использованной литературы:

1. Физика. 8 класс: Учебник для общеобразовательных учреждений /А.В. Перышкин. – М.: Дрофа, 2010.
2. Физика 7-9. Учебник. И.В. Кривченко.
3. Физика. Справочник. О.Ф. Кабардин. – М.: АСТ-ПРЕСС, 2010.

Электрические сети зациклены на передаче электроэнергии от источника к потребителю, которые являются основными элементами цепочки. Но кроме них в электрическую цепь вставляются и другие составляющие, к примеру, управляющие элементы, к которым относится реостат или любой другой прибор с таким же принципом действия. Устройство реостата – это проводник определенного сечения и длины, через которые можно узнать сопротивление проводника. Конечно, обговаривается и его материал. Изменяя сопротивление прибора, а, точнее, проводника, можно регулировать величину силы тока и напряжения в сети. Итак, реостат – это прибор, регулирующий напряжение и ток.

Задачи на Последовательное соединение проводников с решениями

Формулы, используемые на уроках «Задачи на Последовательное соединение проводников»

Задача № 1.
 Два проводника сопротивлением 2 Ом и 3 Ом соединены последовательно. Сила тока в цепи 1 А. Определить сопротивление цепи, напряжение на каждом проводнике и полное напряжение.

ОТВЕТ: 5 Ом;  2 В;  3 В;  5 В.

Задача № 2.
 Два проводника сопротивлением 20 Ом и 30 Ом соединены последовательно. Напряжение на концах первого проводника 12 В. Определить сопротивление цепи, силу тока в цепи, напряжение на втором проводнике и полное напряжение.

ОТВЕТ: 50 Ом;  18 В;  0,6 А;  30 В.

Задача № 3.
 Два резистора соединены последовательно. Сопротивление первого 12 Ом, полное сопротивление 30 Ом. Сила тока в цепи 2 А. Определить сопротивление второго резистора, напряжение на каждом проводнике и полное напряжение.

ОТВЕТ: 18 Ом;   24 В;   36 В;   60 В.

Задача № 4.
 В каких пределах можно менять сопротивление в цепи, если сопротивление реостата R имеет пределы 0…10 Ом? Сопротивление резистора R1 равно 20 Ом.

Указание к решению: Сопротивления R и R1 соединены последовательно., следовательно: R_min = 20 + 0 = 20 (Ом); R_max = 20 + 10 = 30 (Ом).Ответ: от 20 до 30 Ом.

Задача № 5.
Последовательно с нитью накала радиолампы сопротивлением 3,9 Ом включен резистор, сопротивление которого 2,41 Ом. Определите их общее сопротивление.

ОТВЕТ: 6,31 Ом.

Задача № 6.
 Общее сопротивление последовательно включенных двух ламп сопротивлением 15 Ом каждая и реостата равно 54 Ом. Определите сопротивление реостата.

ОТВЕТ: 24 Ом.

Задача № 7.
Два резистора сопротивлением 8 и 1 кОм соединены последовательно. Определите показание вольтметра, подключенного между точками А и С, если сила тока в цепи равна 3 мА. Что будет показывать вольтметр, подключенный между точками А и В, В и С?

ОТВЕТ: 27 В,   24 В;   3 В.

Задача № 8.
 В цепь включены последовательно три проводника сопротивлениями: R1 = 5 Ом, R2 = 6 Ом, R3 = 12 Ом. Какую силу тока показывает амперметр и каково напряжение между точками А и В, если показание вольтметра 1,2 В?

ОТВЕТ: 0,2 А;   4,6 В.

Задача № 9.
 Последовательно с электрической лампой включен реостат. Начертите схему цепи и определите сопротивление реостата и лампы, если напряжение на зажимах цепи 12 В. Вольтметр, подключенный к реостату, показывает 8 В. Сила тока в цепи 80 мА.

ОТВЕТ: 50 Ом.

Задача № 10.
 Вольтметр, подключенный к батарее (см. рис.), показывает напряжение 40 В. Определите напряжение на всех сопротивлениях в цепи.

ОТВЕТ: 12 В, 8 В, 16 В, 4 В.

Задача № 11.
Маленькая электрическая лампочка для елочной гирлянды рассчитана на ток в 0,3 А и имеет сопротивление 20 Ом. Сколько таких лампочек надо соединить последовательно, чтобы гирлянду можно было включить в сеть с напряжением 220 В?

ОТВЕТ: 37 лампочек.

Задача № 12.
 На рисунке изображена цепь с никелиновым проводом АВ длиной 10 м и сечением 1 мм2. Через провод пропущен электрический ток силой 2 А. Рассчитайте напряжение на участках АА₁, АА₂, АА₃, АВ и постройте график зависимости напряжения от длины проводника АВ, откладывая по горизонтальной оси длину проводника, а по вертикальной — напряжение на этой длине.

Задача № 13.
 В цепь последовательно включены два проводника из одного и того же материала сечениями S₁ = 1 мм2 и S₂ = 2 мм2, длины их равны. Определите напряжение на концах каждого проводника, если на концах цепи напряжение равно 120 В.

ОТВЕТ: 80 В;  40 В.

Задача № 14.
Начертите электрическую схему состоящую из источника тока, ключа, лампочки сопротивлением 3 Ом, резистора сопротивление 2 Ом, соединённых последовательно, амперметра и вольтметра, подключенного к резистору. Определите показания амперметра, если показания вольтметра 1,6 В? Что покажет вольтметр, если его подключить к лампочке?

ОТВЕТ: 0,8 А;  2,4 В.

Это конспект по теме «ЗАДАЧИ на Последовательное соединение проводников». Выберите дальнейшие действия:

• Перейти к теме: ЗАДАЧИ на Параллельное соединение проводников
• Посмотреть конспект по теме Соединение проводников
• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

Сопротивление при последовательном и параллельном соединении проводников

Рассмотрим участок цепи AB, представляющий собой последовательное соединение двух резисторов с сопротивлениями R₁ и R₂.

В соответствии с законом Ома полное сопротивление рассматриваемого участка U = IR, где U — общее напряжение на участке цепи АВ, равное сумме напряжений на каждом из резисторов: U = U₁ + U₂.

I — сила тока на участке цепи АВ. Она одинакова на всём участке и равна силе тока I₁ и I₂ в каждом из резисторов. Поэтому можно записать:IR = IR₁ + IR₂,
IR = I(R₁ + R₂).

Следовательно, R = R₁ + R₂.

Общее сопротивление цепи при последовательном соединении равно сумме сопротивлений отдельных проводников.

При последовательном соединении нескольких проводников общее сопротивление цепи равно сумме сопротивлений отдельных проводников: R = R₁ + R₂ + … Rn.

Способ последовательного подключения всё новых участков цепи реализован в работе реостата, о котором говорилось на предыдущих уроках. Передвигая ползунок реостата, мы увеличиваем или уменьшаем число витков проволоки, включённых последовательно в цепь. При этом сопротивление цепи соответственно увеличивается или уменьшается.

При последовательном соединении проводников их общая длина увеличивается. Поэтому сопротивление цепи становится больше сопротивления любого из проводников.

СОПРОТИВЛЕНИЕ ПРИ ПАРАЛЛЕЛЬНОМ СОЕДИНЕНИИ

Рассмотрим участок цепи CD, представляющий собой параллельное соединение двух резисторов с сопротивлениями R₁ и R₂.

В соответствии с законом Ома I = U/R, где R — общее сопротивление рассматриваемого участка цепи; U — общее напряжение на участке цепи CD, равное напряжениям U₁ и U₂ на каждом из резисторов; I — сила тока на участке цепи CD, она равна сумме токов в каждом из резисторов:  I = I₁ + I₂.

Поэтому можно записать:

где R₁ и R₂ — сопротивления первого и второго резисторов соответственно.

Учитывая, что U = U₁ = U₂, получаем

Следовательно,

Для рассмотренного случая двух резисторов, соединённых параллельно, общее сопротивление цепи можно вычислить по формуле

Таким образом, общее сопротивление цепи при параллельном соединении нескольких резисторов можно вычислить из формулы

Уменьшение общего сопротивления проводников при их параллельном соединении объясняется тем, что общая площадь поперечного сечения проводников на данном участке цепи увеличивается.

В используемых на практике электрических цепях часто встречается смешанное соединение проводников, включающее в себя как последовательные, так и параллельные участки. При расчёте таких цепей сначала вычисляют необходимые величины на каждом из участков цепи, а затем находят её общие параметры.

Вы смотрели Конспект по физике для 8 класса «Сопротивление при последовательном и параллельном соединении проводников».

Вернуться к Списку конспектов по физике (Оглавление).

Просмотров:
4 605