Расчет линейных цепей с переменным током

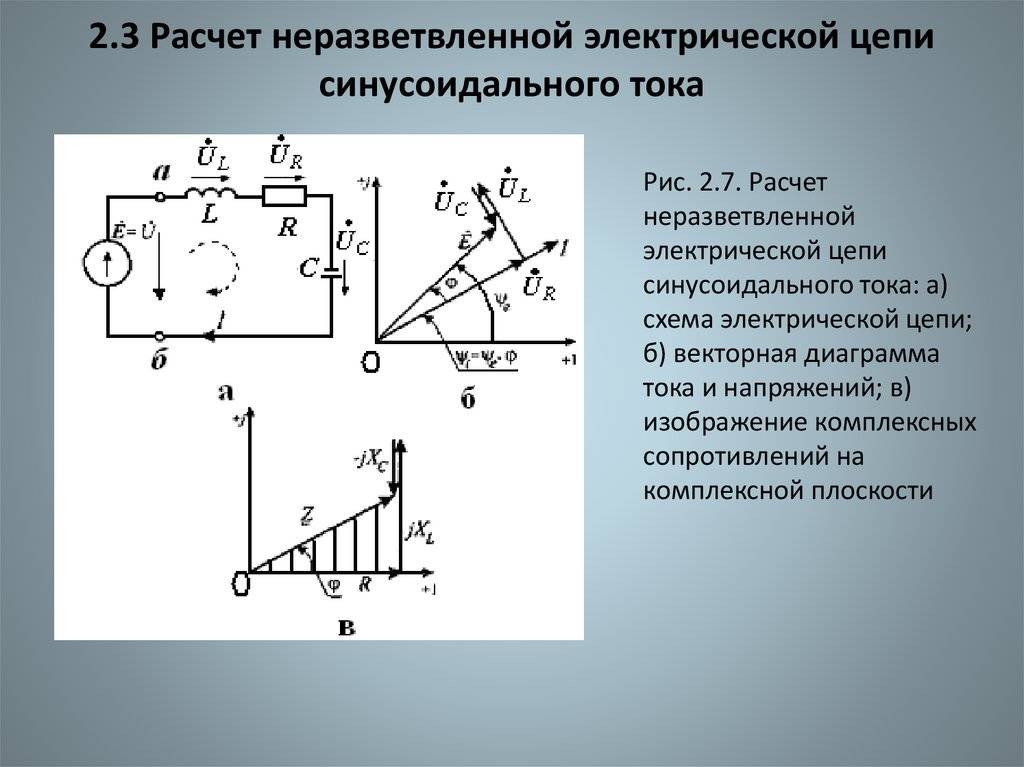
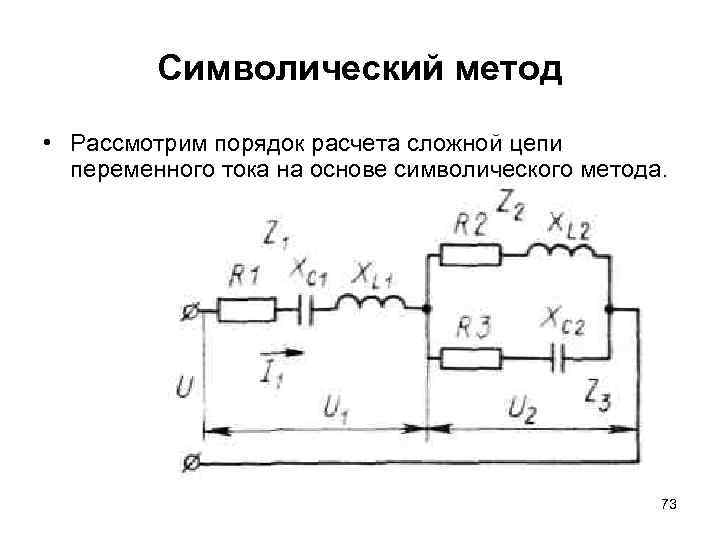
Мощность в цепи с емкостью

Произведение тока и напряжения для емкости дает синусоиду, которая состоит из положительных и отрицательных полуволн, значит, средняя за период мощность равна 0.

Физический смысл состоит в том, что емкость за пол периода получает энергию, а затем пол периода возвращает ее в источник. Энергия накапливается в электрическом поле емкости, а затем возвращается в источник.  Частота синусоиды мощности вдвое больше частоты тока и напряжения.

Таким образом, на емкости не получается выделение тепла и никакой полезной мощности получить нельзя. Поэтому мощность, которая получается на емкости, называется реактивной и обозначается буквой – Qc.

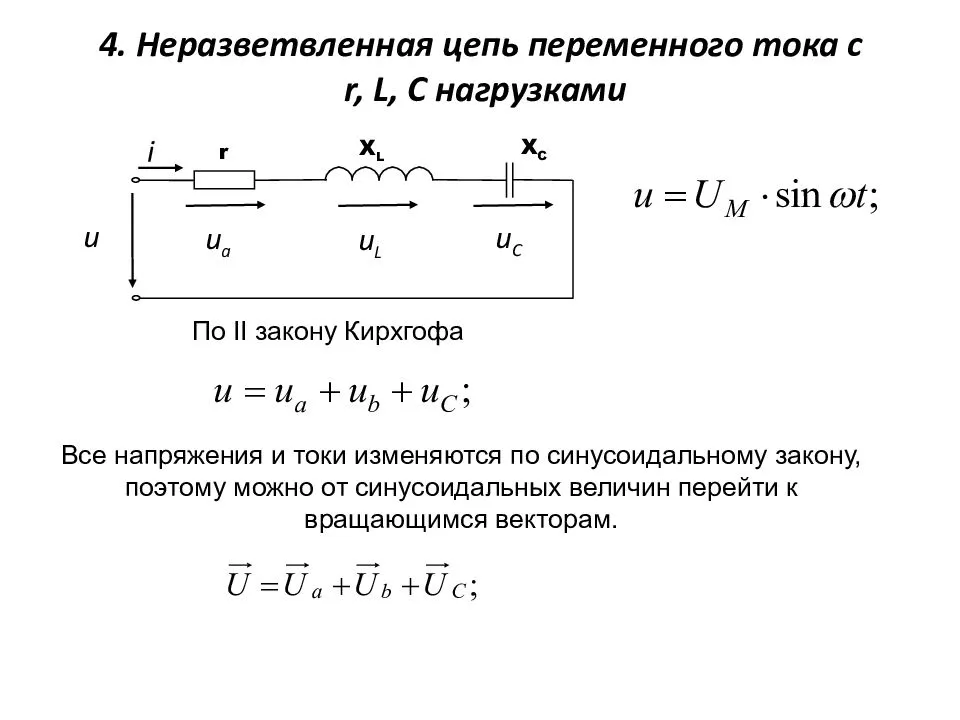
Цепи RLC

Цепи, которые содержат R, L и C, могут иметь разные варианты соединений. Цепи могут быть последовательными, разветвленными, и имеющие последовательные соединения в ветвях. Рассмотрим простые варианты. RLC последовательно.

В некоторых случаях цепи RL (моторы, трансформаторы и т. п.) имеют слишком маленький Cos φ. То есть в них слишком сильно влияние индуктивной составляющей. В такие цепи специально включают компенсационные конденсаторы, которые уменьшают фазовый сдвиг, Это разгружает источники электроэнергии от избыточной реактивной нагрузки, и обеспечивает значительную экономию электроэнергии.

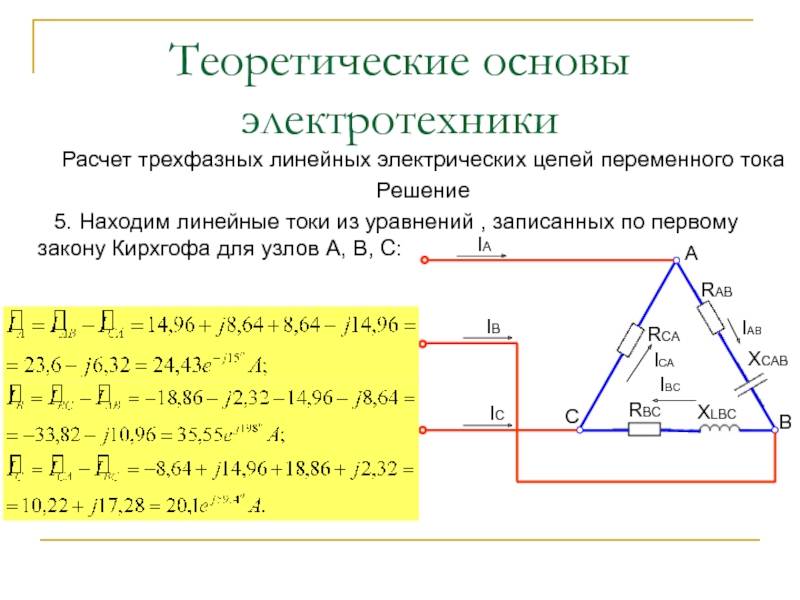
Несимметричная нагрузка при соединении приемников звездой

Нагрузка трехфазной электрической сети будет считаться несимметричной, если хотя бы одно из фазных сопротивлений не равно другим. Проще говоря, сопротивления фаз не равны, например: r_a = r_b = r_c, x_a = x_b ≠ x_c. В общем случае  считают, что несимметричная нагрузка возникает при отключении одной из фаз.

Возникает не симметрия чаще всего при подключении к трехфазной сети однофазных электроприемников. Они могут иметь различные мощности, режимы работы, различное территориальное расположение, что тоже влияет на величину фазной нагрузки.

В случае, когда необходимо подключить однофазные потребители электрической энергии, для более равномерной загрузки их делят на три примерно одинаковые по мощности группы.

Один вывод однофазных потребителей подключают к одной из трех фаз, а второй вывод подключают к нейтральному проводу. Так как все электроприемники рассчитываются на одно напряжение, то в пределах каждой фазы они соединяются параллельно.

Главной особенностью электрической сети несимметричной нагрузкой является то, что она должна в обязательном порядке иметь нейтральный провод. Это объяснимо тем, что при его отсутствии величины фазных напряжений будут в значительной степени зависеть от величины не симметрии сети, то есть от величин и характера сопротивления каждой из фаз. Поскольку сопротивления фаз могут варьироваться довольно в широких пределах в зависимости от количества подключенных электроприемников, также широко будет варьироваться и напряжения на потребителях электрической энергии, а это недопустимо.

Для иллюстрации выше сказанного ниже приведена векторная диаграмма для трехфазной несимметричной цепи при наличии нейтрального провода:

Ниже приведена приведена векторная диаграмма для этой же цепи, но при отсутствии нулевого рабочего (нейтрального) провода:

Также можно посмотреть видео, где объясняется, что может произойти в электрической цепи при обрыве нулевого провода:

Обрыв нуля в цепи переменного тока.

Необходимость нулевого провода станет еще более очевидной, если представить, что вам необходимо подключить однофазного потребителя к одной из фаз, при этом остальные две подключать нельзя, так как приемник рассчитан на фазное напряжение 220 В, а не на линейное 380В, как в таком случае получить замкнутый контур для протекания электрического тока? Только использовать нулевой рабочий проводник.

Для повышения надежности соединения электроприемников в цепь нулевого рабочего проводника не устанавливают коммутационную аппаратуру (автоматические выключатели, предохранители или разъединители).

Фазные токи, углы сдвига, а также фазные мощности при несимметричной нагрузке будут различными. Для вычисления их фазных значений можно применить формулу (5), а вот для вычисления трехфазной мощности формула (6) уже не подходит. Для определения мощностей необходимо пользоваться выражением:

Если существует необходимость определения тока нейтрального провода, то необходимо решать задачу комплексным методом. Если существует векторная диаграмма, то определить ток можно по ней.

Пример

В осветительной электрической сети с напряжением в 220 В в фазе А включено 20 ламп, фазе В – 10 ламп, а в фазе С – 5 ламп. Параметры лампы U_ном = 127 В, Р_ном = 100 Вт. Необходимо определить ток нейтрального провода и каждой лампы.

Решение

Если учесть, что лампы накаливания имеют только активное сопротивление (реактивное слишком мало и им пренебрегают), то по формуле мощности определим ток лампы, а по закону Ома ее сопротивление:

Зная число и сопротивление ламп нетрудно определить сопротивления фаз, а также фазные токи:

Для определения тока в нейтральном проводе I_N решим задачу комплексным методом. Так как при сделанных ранее допущениях комплексные напряжения приемника равны комплексным ЭДС источника, получим:

Где комплексные значения фазных сопротивлений будут равны Z_a = 8,05 Ом, Z_b = 16,1 Ом, Z_с = 32,2 Ом.

Комплексные значения токов, а также действующее значение тока нейтрального провода будут иметь вид:

Что это такое

Полная мощность (ВА, кВА) характеризуется потребляемой нагрузкой (например, ИБП) двух составляющих, а также отклонением формы электрического тока и напряжения от гармонической. С мощностью электротока человеку приходится сталкиваться и в быту и на производстве, где применяются электрические приборы. Каждый из них потребляет электроток, поэтому при их использовании всегда необходимо учитывать возможности этих приборов, в том числе заложенные в них технические характеристики.

Советуем изучить — Дуговая сталеплавильная печь

Значение полной мощности — вычисление формулы

Чтобы определить работу мощности за одну секунду, на практике применяется формула для производительности постоянного тока. Следует отметить, что данная физическая величина меняется во времени и для выполнения практического расчета совершенно бесполезна. Для вычисления среднего значения производительности требуется интегрирование по времени.

Обратите внимание! С целью определения данного показателя в электрической цепи, где периодически происходит смена напряжения и тока, средняя ёмкость вычисляется по передаче мгновенной мощности в течение определённого времени. Как вычисляется ёмкость по другой формуле. Как вычисляется ёмкость по другой формуле

Как вычисляется ёмкость по другой формуле

Есть определенная категория людей, которая интересуется вопросом, какая бывает мощность. Активная производительность делится на следующие категории: фактическую, настоящую, полезную, реальную.

Ёмкость, преобладающая в электрических цепях постоянного тока, которая при этом получает нагрузку постоянного тока, определяется простым произведением напряжения по показателям нагрузки и потребляемого тока. Данная величина вычисляется по формуле: P = U х I. Данный результат показывает, что фазовый угол между током и напряжением отсутствует в электрических цепях постоянного тока. То есть отсутствует коэффициент производительности.

Синусоидальный сигнал намного усложняет процесс. Так как фазовый угол между током и напряжением может значительно отличаться друг от друга. Поэтому среднее значение определяется по следующей формуле:

P = U I Cosθ

Важно! Если в соединениях переменного тока фиксируется активная (резистивная) производительность, тогда для вычисления данного показателя применяется формула следующего характера: P = U х I. Мощность трёхфазной цепи. Мощность трёхфазной цепи

Мощность трёхфазной цепи

Пример реальной цепи

Самую простую электрическую цепь можно сделать самостоятельно. Её часто собирают на уроке физики. При этом не стоит опасаться поражения током, так как в ней будет использоваться низковольтный источник напряжения. Но всё же перед тем как приступить к сборке, следует знать о коротком замыкании. Под ним понимают состояние, при котором происходит закорачивание выхода.

Другими словами, вся энергия источника тока оказывается приложенной к нему же. В результате разность потенциалов снижается до нуля, а в цепи возникает максимальная сила тока. Непреднамеренное короткое замыкание может привести к выходу из строя генератор и радиодетали. Именно для защиты от этого пагубного воздействия в цепи ставят предохранитель.

Схема для самостоятельного повторения будет представлять собой узел управления освещением. Для её сборки необходимо подготовить:

Источник питания на 12 вольт. Это может быть аккумулятор, регулируемый лабораторный блок, батарейки. Главное, чтобы источник смог выдавать нужное напряжение. Например, нужную величину можно получить соединив последовательно несколько батареек со стандартным номиналом 1,5 В (1,5 * 4 = 12 В).
Лампочка

Подойдёт накаливания
Здесь важно обратить внимание на её характеристики. Она должна быть рассчитанной на нужное напряжение.
Ключ
Это обыкновенный выключатель, имеющий два устойчивых состояния — разомкнутое и замкнутое.
Провода

В сборке можно использовать любые медные проводники сечением от 0,25 мм 2 .

Электрическая цепь включает (в общем случае): источник питания, рубильник (выключатель), соединительные провода, потребителей. Обязательно сформируйте замкнутый контур. В противном случае по цепи не сможет течь ток. Электрическими не принято называть контуры заземления, зануления. Однако по сути считаются таковыми, иногда здесь течет ток. Замыкание контура при заземлении, занулении обеспечивается посредством грунта.

Источники питания. Внутренняя, внешняя электрическая цепь

Для образования упорядоченного движения носителей заряда, формирующего ток, потрудитесь создать разность потенциалов на концах участка. Достигается подключением источника питания, который в физике принято называть внутренней электрической цепью. В противовес прочим элементам, составляющим внешнюю. В источнике питания заряды движутся против направления поля. Достигается приложением сторонних сил:

1. Обмотка генератора.
2. Гальванический источник питания (батарейка).
3. Выход трансформатора.

Напряжение, формируемое на концах участка электрической цепи, бывает переменным, постоянным. Сообразно в технике принято контуры делить соответствующим образом. Электрическая цепь предназначена для протекания постоянного, переменного тока. Упрощенное понимание, закон изменения упорядоченного движения носителей заряда воспринимается сложным. С трудом понимаем, переменный в цепи ток или постоянный.

Род тока определен источником, характером внешней электрической цепи. Гальванический элемент дает постоянное напряжение, обмотки (трансформаторы, генераторы) – переменное. Связано с протекающими в источнике питания процессами.

Сторонние силы, обеспечивающие движения зарядов, называют электродвижущими. Численно ЭДС характеризуется работой, совершаемой генератором для перемещения единичного заряда. Измеряется вольтами. На практике для расчета цепей удобно делить источники питания двумя классами:

1. Источники напряжения (ЭДС).
2. Источники тока.

В действительности неизвестны, имитацию пытаются создать практики. В розетке ожидаем увидеть 230 вольт (220 вольт по старым нормативам). Причем ГОСТ 13109 однозначно устанавливает пределы отклонения параметров от нормы. В быту пользуемся источником напряжения. Параметр нормируется. Величина тока не играет значения. Напряжение подстанции круглые сутки стремятся сделать постоянным вне зависимости от текущего запроса потребителей.

В противовес источник тока поддерживает заданный закон упорядоченного движения носителей заряда. Значение напряжения роли не играет. Ярким примером подобного рода устройств выступает сварочный аппарат на базе инвертора. Каждый знает: диаметр электрода прочно связан с толщиной металла, прочими факторами. Чтобы процесс сварки шел правильно, приходится с высокой степенью постоянства поддерживать ток. Задачу решает электронный блок на основе инвертора.

Ток, напряжение бывают постоянными, переменными. Закон изменения параметра роли не играет

Неважно, подключать ли электрическую цепь к источнику постоянного, переменного напряжения. Однако важно выдержать правильный размер параметра

К примеру, действующее значение ЭДС.

Мощность при переменном токе

Предположим, что имеется потребитель электрической энергии (рис. 1.9.), напряжение и ток которого известны

u= Um sin(ωt+ψu), i= Im sin ωt

Рис. 1.9. Схема и векторная диаграмма потребителя

На рис. 1.9,б

приведена векторная диаграмма потребителя. В зависимости от характера нагрузки, т.е. характера сопротивлений потребителя, угол сдвига фаз между напряжением и током

φ = ψu – ψi

может лежать в пределах от π/2 до –π/2. В рассматриваемом случае φ=ψu так как ψi=0.

При переменном токе различают следующие мощности: мгновенную, активную, реактивную и полную (кажущуюся).

Под мгновенной понимается мощность, равная произведению мгновенных значений напряжения и тока:

P=u·i

С течением времени мгновенная мощность изменяется как по величине, так и по знаку.

При активной нагрузке (рис. 1.10,а, φ=0) в течение всего периода изменения тока мгновенная мощность положительна. В этом случае электрическая энергия забирается из сети и обратно в сеть не возвращается. Она преобразуется в тепло, в механическую энергию и т.д.

При индуктивной нагрузке (рис. 1.10,а, φ=π/2) в одну четверть периода изменения тока мгновенная мощность положительна, в другую – отрицательна. Соответственно, в одну четверть периода электрическая энергия забирается из сети и преобразуется в энергию магнитного поля, в другую – такое же количество энергии преобразуется из энергии магнитного поля, в электрическую энергию и возвращается в сеть.

В случае емкостной нагрузки (рис. 1.10,в, φ= — π/2) в одну четверть периода электрическая энергия забирается из сети и преобразуется в энергию электрического поля, в другую – энергия электрического поля преобразуется в электрическую энергию и возвращается в сеть.

В случае смешанной активно-индуктивной (0<�φ<�π/2) или активно-емкостной нагрузки (0<�φ< — π/2) забираемая из сети электрическая энергия больше энергии, возвращаемой в сеть. В сеть возвращается только та часть энергии, которая была преобразована в энергию магнитного или электрического поля.

Рис. 1.10. Графики тока, напряжения и мощности при различных нагрузках

Под активной понимается мощность, равная среднему значению мгновенной мощности за период

Если разложить ток потребителя на составляющие (рис. 1.9, б), то получим

где — активная составляющая тока

где — реактивная составляющая тока

Активную мощность можно выразить следующим образом

Активная мощность обусловлена совпадающими по фазе напряжением и током. Входящий в выражение мощности cosφ получил название коэффициент мощности. Чем больше cosφ потребителя, тем больше будет при неизменных токе и напряжении активная составляющая тока и активная мощность. Когда φ = π/2 или φ = — π/2 (рис. 1.10,б,в) cosφ и активная мощность равна нулю.

Реактивная мощность (индуктивная или емкостная) выражается следующим образом

Q=U·I·sin φ

Реактивная мощность обусловлена током и напряжением, сдвинутым по фазе на угол φ=±π/2.

Реактивная мощность соответствует энергии, которая в одну четверть периода забирается из сети и преобразуется потребителем в энергию магнитного или электрического поля, а в другую – вновь преобразуется в электрическую энергию и возвращается в сеть.

Полная (кажущаяся) мощность включает в себя активную и реактивную мощности и равна

S=U·I

Между активной, реактивной и полной мощностями существуют соотношения

Все перечисленные мощности имеют одну и ту же размерность:

вольт х ампер (В·А). Однако, для того, чтобы различать эти мощности, единицы их измерения называют по-разному:

ед. P = 1 Вт – ватт;

ед. Q = 1 ВАр – вольтампер реактивный;

ед. S = 1 ВА – вольтампер.

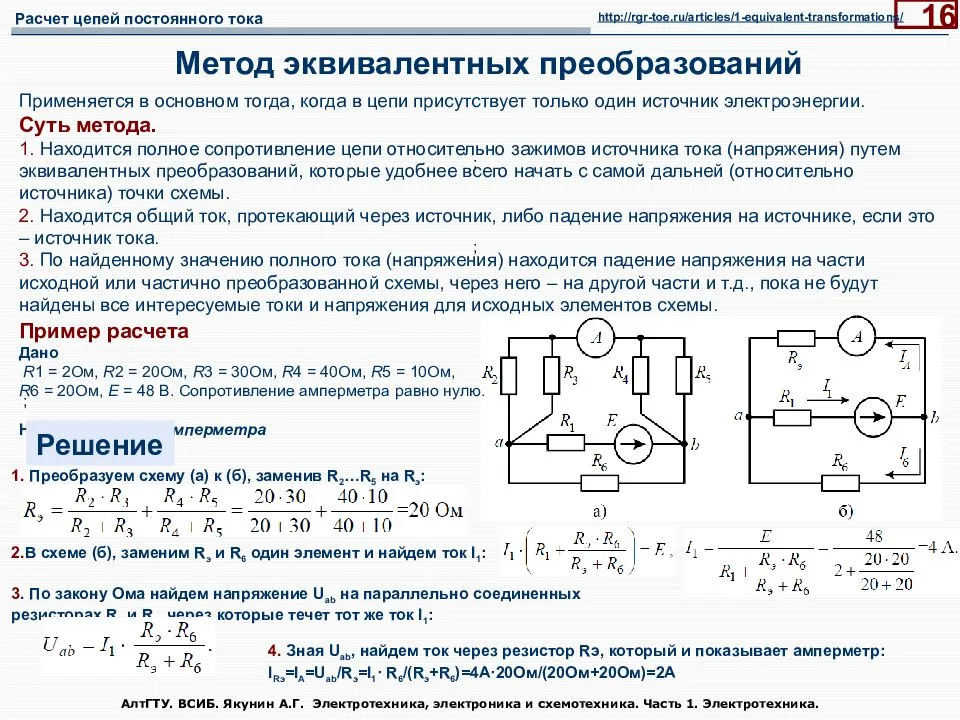
Метод узловых (потенциалов) напряжений

ТОЭ › Методы расчета цепей постоянного тока

При изучении основ электротехники приходится сталкиваться с необходимостью расчета тех или иных параметров различных схем. И самое простое, что приходится делать – это расчет токов ветвей в цепях постоянного тока.

Существует несколько наиболее применяемых методов расчетов для таких цепей: с помощью законов Кирхгофа, методом контурных токов, узловых потенциалов, методом эквивалентного генератора, эквивалентного источника тока, методом наложения. Для расчета более сложных цепей, например, в нелинейных схемах, могут применяться метод аппроксимации, графические методы и другие. В данном разделе рассмотрим один из методов определения токов в цепи постоянного тока – метод узловых потенциалов.

Важно отличать метод узловых напряжений (потенциалов) от метода узлового напряжения (метод двух узлов)

Метод узловых потенциалов примеры решения задач

Для того, чтобы лучше разобраться в этом вопросе, рассмотрим конкретный пример схемы, показанной на рис.1.

Рис.1. Схема постоянного тока

Для начала обозначают направления токов в ветвях. Направление можно выбирать любым. Если в результате вычислений какой-то из токов получится с отрицательным значением, значит, его направление в действительности будет направлено в противоположную сторону относительно ранее обозначенного. Если в ветви имеется источник, то для удобства лучше обозначить направление тока в этой ветви совпадающим с направлением источника в этой ветви, хотя и не обязательно. Далее один из узлов схемы заземляем. Заземленный узел будет называться опорным, или базисным. Такой метод заземления на общее токораспределение в схеме влияния не оказывает.

Какой именно узел заземлять, значения не имеет. Заземлим, например, узел 4 φ4 = 0.

Каждый из этих узлов будет обладать своим значением потенциала относительно узла 4. Именно значения этих потенциалов для дальнейшего определения токов и находят. Соответственно, для удобства этим потенциалам присваивают номера в соответствии с номером узла, т.е. φ1, φ2, φ3. Далее составляется система уравнений для оставшихся узлов 1, 2, 3.

В общем виде система имеет вид:

Использованные в этой системе уравнений буквенно-цифровые обозначения

имеют следующий смысл:

– сумма проводимостей ветвей, сходящихся в узле 1. В данном случае

– сумма проводимостей ветвей, сходящихся в узле 2. В данном случае

– сумма проводимостей ветвей, сходящихся в узле 3. В данном случае

– сумма проводимостей ветвей, соединяющих узлы 1 и 2, взятая со знаком «минус». Для этого единица и взята с отрицательным знаком:

– сумма проводимостей ветвей, соединяющих узлы 1 и 3, взятая со знаком «минус». Для этого единица и в этом случае взята с отрицательным знаком:

Аналогично находятся и остальные проводимости:

J11 – узловой ток узла 1, в котором участвуют ветви, подходящие именно к этому узлу, и содержащие в своем составе ЭДС. При этом, если ЭДС ветви, входящий в узел, направлена к рассматриваемому узлу (в данном случае к узлу 1), то такой узловой ток записывается с плюсом, если от узла, то с минусом. В данном случае

Аналогично

В результате всех ранее приведенных вычисленных значений исходная система уравнений примет вид:

Решать данную систему можно всеми доступными методами, мы же для упрощения решим ее в пакете Mathcad:

В результате получены следующие значения потенциалов в узлах цепи:

Токи в ветвях находятся в соответствии с законом Ома. Поясним это простыми словами.

В ветви с сопротивлением и источником, учитывая ранее обозначенное направление тока в рассматриваемой ветви, необходимо из потенциала узла, находящегося у начала стрелки направления тока, вычесть потенциал узла, находящегося у конца стрелки направления тока, а затем прибавить значение ЭДС в этой ветви. Далее все это разделить на сопротивление, имеющееся в ветви. Если бы ток и ЭДС в рассматриваемой ветви не совпадали по направлению, тогда значение ЭДС вычиталось. В ветви без ЭДС действует то же самое правило, только ЭДС в числителе, разумеется, отсутствует. В нашем примере получим, что

Значение тока первой ветви, как видно из расчета, получилось отрицательным. Значит, в действительности, этот ток направлен в противоположную сторону относительно его обозначенного направления на рис.1.

Правильность расчетов можно проверить, например, составлением баланса мощностей либо, к примеру, моделированием, схемы. Выполним моделирование в программе Multisim.

Рис.2. Моделирование в Multisim

Как видим, результаты моделирования совпадают с расчетными значениями. Незначительная разница в тысячных долях из-за округлений промежуточных вычислений.

Основные методы расчета цепей переменного тока и их задачи

Расчет цепей переменного тока решает те же задачи, что и расчет цепей постоянного тока: определение характеристик цепи и (или) законов их изменения.

Переменный ток описывают с помощью периодических функций — косинуса или синуса. Чаще всего используют синусоидальную форму представления сигнала.

В электротехнике используют комплексные числа и комплексную форму записи переменного тока. Все рассмотренные методы расчета цепей постоянного тока применимы и для цепей переменного тока с той лишь разницей, что все выражения и законы будут записываться в комплексной форме.

Запишем первый закон Кирхгофа в комплексном виде: алгебраическая сумма комплексов токов в узле равна нулю.

Второй закон Кирхгофа: в контуре алгебраическая сумма комплексов падений напряжений на пассивных элементах равна алгебраической сумме комплексов ЭДС и напряжений источников энергии.

Также при расчете цепей учитывают, что в цепях переменного тока полное сопротивление Z состоит из действительной части R и мнимой — jx.

Мнимую часть сопротивления называют реактивным сопротивление и рассчитывают как разницу между реактивными сопротивлениями индуктивного xL и емкостного элементов xC.

Кривые напряжения и тока в активном сопротивлении

Величину переменного напряжения или тока можно оценить значением амплитуды или средним значением за полупериод или действующим значением. При изменении напряжения или тока по закону синуса среднее значение напряжения определяется:

При большой частоте вращения ротора генератора, т. е. при большой частоте колебаний э. д. с. и силы тока, измерять их амплитуды на практике крайне неудобно. По этой причине ввели величины, названные действующими значениями э. д. с, силы тока и напряжения.

Действующим значением силы переменного тока называют силу такого постоянного тока, при прохождении которого по той же цепи и за то же время выделяется такое же количество теплоты, как и при прохождении переменного тока.

откуда

При синусоидальном законе действующие значения тока и напряжения:

Приборы электромагнитной системы, применяемые для измерений напряжений и токов на переменном токе, регистрируют действующие значения. Соответственно градуируются и шкалы этих приборов.

Ток, протекающий через индуктивность L (рис. 7), меняется по закону синуса /’ = Im sin(co/ + у;).

Метод векторных диаграмм

Мы уже пользуемся векторными диаграммами, по которым наблюдаем соотношения токов и напряжения в цепях переменного тока. Векторная диаграмма это стоячее изображение вращающихся векторов.

В предыдущих рассуждениях, было сказано, что линейно развернутая диаграмма переменного процесса, (в простом случае синусоидального), точно показывает  изменение мгновенного значения переменной величины, то есть происходит все именно так как показывает синусоида и каждая ее точка и есть переменная величина в данный момент. Но оказывается нам интересно не это, нам нужно знать какое значение тока и напряжения и мощности действует в цепи в течение времени, то есть действует длительное время, пока цепь работает.

Анализ синусоид нескольких величин, одновременно действующих в разных фазах, позволяет рассчитать все свойства и режимы работы цепи переменного тока, но гораздо проще это сделать, если отвлечься от синусоид и просто построить соотношение векторов, которые, собственно, и образуют эти синусоиды. Вся информация синусоид заложена в их радиус – векторах. Мы останавливаем эти векторы на рисунке, понимая, что они вращающиеся, но факт их вращения учитываем угловой частотой в расчетных формулах векторной диаграммы.

Итак, векторная диаграмма заменяет линейно развернутую синусоидальную диаграмму, потому, что любая информация, заложенная в синусоиду, есть и в соответствующем ей радиус-векторе.

Если нам приходится рассматривать несколько действующих одновременно синусоидальных процессов, то они изображаются векторной диаграммой, где длина каждого вектора, соответствует действующему значению синусоидальной величины, направление вектора соответствует начальной фазе, синусоидальной величины.

Результирующие значения одновременно действующих напряжений рассчитывается как векторная сумма, где угол между векторами определяется сдвигом фаз между ними.

Расчет цепей переменного тока сводится к расчету треугольников, которые состоят из соответствующих векторов.

Например, можно определить суммарное напряжение, частичные напряжения, и сдвиг фаз между ними.

На основании векторных диаграмм можно построить подобные векторным диаграммам треугольники сопротивлений и треугольники мощностей, решением которых можно определить соотношения сопротивлений, и мощности которые действуют в цепях переменного тока.

Векторная диаграмма напряжений представляет собой векторный треугольник напряжений

Последовательное соединение L R.

Любая катушка наматывается проволокой, а проволока обладает сопротивлением, которое приходится учитывать.

Получается, что реальная цепь, содержащая только L, просто невозможна. В некоторых случаях значением R пренебрегают, и получается, что вроде бы цепь с только L, на самом деле она конечно L R.

Реально, кроме проволоки, в цепи всегда есть и какие – то другие элементы R, поэтому интерес представляют именно цепи L R,

Ток, при последовательном соединении, один и тот же через все сопротивления, а напряжения разные, но общее напряжение не равно просто сумме напряжений на каждом сопротивлении, оно равно векторной сумме, то есть вектор общего напряжения равен сумме векторов напряжений на каждом участке. Для расчетов напряжений надо построить векторную диаграмму.

Векторная диаграмма строится так.

Метки

• алгоритм расчет цепей при несинусоидальных периодических воздействиях
• алгоритм расчета цепей периодического несинусоидального тока
• баланс мощностей
• ВАХ нелинейного элемента
• Векторная диаграмма
• ветви связи
• взаимная индуктивность
• взаимная проводимость
• вольт-амперная характеристика нелинейного элемента
• второй закон Кирхгофа
• второй закон Кирхгофа для магнитных цепей
• входная проводимость
• гармоники напряжения
• гармоники тока
• Генератор напряжения
• генератор тока
• главные контуры
• графический метод расчета нелинейных электрических цепей
• динамическое сопротивление
• дифференциальное сопротивление
• емкость двухпроводной линии
• емкость коаксиального кабеля
• емкость конденсатора
• емкость однопроводной линии
• емкость плоского конденсатора
• емкость цилиндрического конденсатора
• закон Ампера
• закон Био Савара Лапласа
• закон Ома
• закон полного тока
• закон электромагнитной индукции
• Законы Кирхгофа
• индуктивность
• индуктивность двухпроводной линии
• индуктивность однопроводной линии
• индуктивность соленоида
• катушка со сталью
• Конденсатор в цепи постоянного тока
• контурные токи
• коэффициент амплитуды
• коэффициент гармоник
• коэффициент искажения
• коэффициент магнитной связи
• коэффициент мощности трансформатора
• коэффициент трансформации
• коэффициент формы
• кусочно-линейная аппроксимация
• магнитная постоянная
• магнитная цепь
• магнитный поток рассеяния
• метод активного двухполюсника
• метод двух узлов
• метод контурных токов
• метод наложения
• метод узловых напряжений
• метод узловых потенциалов
• метод эквивалентного генератора
• метод эквивалентного источника ЭДС
• Метод эквивалентных преобразований
• методы расчета магнитных цепей
• независимые контуры
• нелинейный элемент
• несинусоидальный периодический ток
• обобщенный закон Ома
• опорный узел
• основной магнитный поток
• параллельное соединение конденсаторов
• первый закон Кирхгофа
• первый закон Кирхгофа для магнитных цепей
• последовательное соединение конденсаторов
• последовательный колебательный контур
• постоянная составляющая тока
• потери в меди
• потери в стали
• приведенный трансформатор
• Примеры расчета схем при несинусоидальных периодических воздействиях
• принцип взаимности
• принцип компенсации
• расчет гармоник тока
• расчет магнитной цепи
• расчет нелинейных цепей постоянного тока
• расчет цепей несинусоидального тока
• Расчет цепи конденсаторов
• расчет цепи с несинусоидальными периодическими источниками
• Резонанс в электрической цепи
• решение задач магнитные цепи
• сила Ампера
• сила Лоренца
• Символический метод
• собственная проводимость
• статическое сопротивление
• сферический конденсатор
• теорема об эквивалентном источнике
• теорема Тевенена
• топографическая диаграмма
• Трансформаторы
• трехфазная система
• удельная энергия магнитного поля
• уравнения трансформатора
• Цепи с конденсаторами
• частичные токи
• чередование фаз
• ЭДС самоиндукции
• эквивалентная схема трансформатора
• электрическая постоянная
• электроемкость
• энергия магнитного поля