Напряжение между концами проводника равно 12в сила тока

1 вариант

1. За 20 минут через утюг проходит электрический заряд 960 Кл. Определите силу тока в утюге.

1) 0,6 А
2) 0,8 А
3) 48 А
4) 1920 А

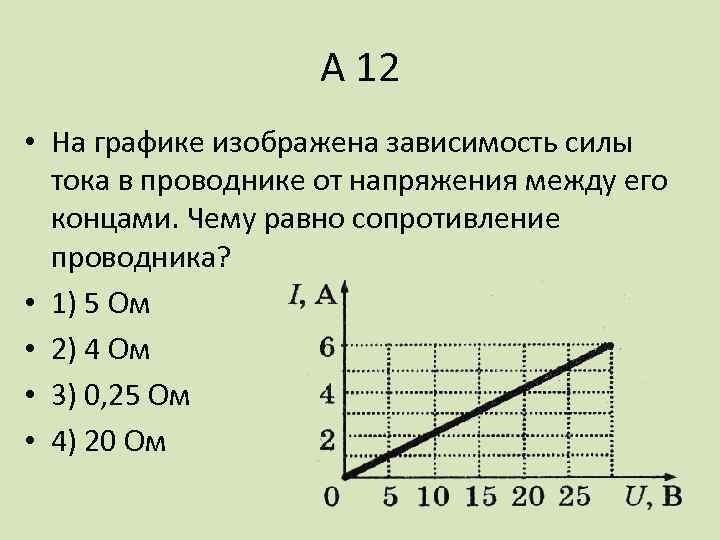
2. На рисунке изображён график зависимости силы тока от напряжения на одной секции телевизора. Каково сопротивление этой секции?

1) 250 кОм
2) 0,25 Ом
3) 10 кОм
4) 100 Ом

3. Если увеличить в 2 раза напряжение между концами проводника, а площадь его сечения уменьшить в 2 раза, то сила тока, протекающего через проводник,

1) увеличится в 2 раза
2) уменьшится в 2 раза
3) не изменится
4) увеличится в 4 раза

4. Сопротивление участка цепи, изображённого на рисунке, равно

1) 3 Ом
2) 5 Ом
3) 8 Ом
4) 21 Ом

5. На штепсельных вилках некоторых бытовых электриче­ских приборов имеется надпись: «6 А, 250 В». Опреде­лите максимально допустимую мощность электроприбо­ров, которые можно включать, используя такие вилки.

1) 1500 Вт
2) 41,6 Вт
3) 1,5 Вт
4) 0,024 Вт

6. Чему равно время прохождения тока по проводнику, если при напряжении на его концах 120 В совершается работа 540 кДж? Сопротивление проводника 24 Ом.

1) 0,64 с
2) 1,56 с
3) 188 с
4) 900 с

7. У становите соответствие между физическими величинами и формулами, по которым эти величины определяются. К каждой позиции первого столбца подберите соответ­ствующую позицию второго.

Физическая величина

А) Сила тока
Б) Напряжение
В) Сопротивление

Формула

1) A/q
2) I2 · R
3) ρl/S
4) I · U · t
5) q / t

8. С помощью кипятильника, имеющего КПД 90%, нагре­ли 3 кг воды от 19 °С до кипения за 15 минут. Какой ток при этом потреблял кипятильник в сети напряжением 220 В? Удельная теплоёмкость воды 4200 Дж/(кг · °С).

Физические формулы и примеры вычислений

Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:

• параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
• последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.

У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.

Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:

• R1 = 1 Ом;
• R2 = 2 Ом;
• R3 = 3 Ом;
• R4 = 6 Ом;
• R5 = 9 Ом;
• R6 = 18 Ом;
• R7 = 2Ом;
• R8 = 2Ом;
• R9 = 8 Ом;
• R10 = 4 Ом.

Напряжение, поданное на схему:

U = 24 В.

Требуется рассчитать токи на всех резистивных элементах.

Исходная цепь

Для расчётов применяется закон Ома:

I = U/R, подставляя вместо R эквивалентное сопротивление.

Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте. Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения

Делают расчёты для каждого такого звена, после – всей цепи целиком

Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.

На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:

• АВ – участок, имеющий две параллельных ветви;
• ВС – отрезок, вмещающий в себя последовательное сопряжение;
• CD – отрезок схемы с расположением трёх параллельных цепочек.

Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.

Последовательно соединённые резисторы R2 и R3

Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.

Смешанное включение на участке CD

Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:

• Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
• Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
• Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.

Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.

Результат первого свёртывания

Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:

• Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
• Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
• 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.

В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.

Результат последующего свёртывания

Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:

Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.

Далее, используя закон Ома, находят ток в последнем последовательном участке:

I = U/ Rэкв. = 24/56,83 = 0,42 А.

Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:

• UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
• UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
• UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.

Следующим шагом станет определение токов на параллельных отрезках AB и CD

• I1 = UAB/R1 = 0,35/1 = 0,35 А;
• I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
• I3 = UCD/R6 = 0,17/18 = 0,009 А;
• I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
• I7 = UCD/R10 = 0,17/4 = 0,04 А.

Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.

U9 = R9*I6 = 8*0,02 = 0,16 В.

Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.

U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.

После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:

• I4 = U7,8/R7 = 1/2 = 0,5 A;
• I5 = U7,8/R8 = 1/2 = 0,5 A.

Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.

Вариант 3

1. Время разряда молнии равно 3 мс. Сила тока в канале молнии около 30 кА. Какой заряд проходит по каналу молнии?

1) 90 Кл
2) 0,1 мкКл
3) 90 кКл
4) 0,1 мКл

2. На рисунке изображен гра­фик зависимости силы тока в проводнике от напряжения на его концах. Чему равно сопротивление проводника?

1) 0,25 Ом
2) 2 Ом
3) 8 Ом
4) 4 Ом

3. Если уменьшить в 2 раза напряжение между концами проводника, а его длину увеличить в 2 раза, то сила то­ка, протекающего через проводник

1) не изменится
2) уменьшится в 4 раза
3) увеличится в 4 раза
4) увеличится в 2 раза

4. Сопротивление участка цепи, изображенного на рисунке, равно

1) 9 Ом
2) 8 Ом
3) 4 Ом
4) 3 Ом

5. На корпусе электродрели укреплена табличка с надпи­сью: 220 В, 500 Вт. Найдите силу тока, потребляемого электродрелью при включении в сеть.

1) 55 000 А
2) 2,27 А
3) 1,14 А
4) 0,88 А

6. Какую работу совершит электрический ток в течение 2 минут, если сила тока в проводнике 4 А, а его сопротивление 50 Ом?

1) 1600 Дж
2) 96 кДж
3) 24 кДж
4) 400 Дж

7. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются. К каждой позиции первого столбца подберите соответствующую позицию второго.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА

А) Сила тока
Б) Напряжение
В) Сопротивление

ФОРМУЛА

1) ρl/_S
2) I2R
3) A/q
4) q/t
5) IUt

Запишите выбранные цифры под соответствующими буквами.

8. Кипятильник нагревает 1,2 кг воды от 12 °С до кипения за 10 минут. Определите ток, потребляемый кипятиль­ником, если он рассчитан на напряжение 220 В. КПД кипятильника 90%. Удельная теплоемкость воды 4200 Дж/(кг·°С).

Как зависит сила тока в проводнике от сопротивления этого проводника

Различные действия тока, такие, как нагревание проводника, магнитные и химические действия, зависят от силы тока. Изменяя силу тока в цепи, можно регулировать эти действия. Но чтобы управлять током в цепи, надо знать, от чего зависит сила тока в ней. Мы знаем, что электрический ток в цепи — это упорядоченное движение заряженных частиц в электрическом поле. Чем сильнее действие электрического поля на эти частицы, тем, очевидно, и больше сила тока в цепи. Но действие поля характеризуется физической величиной — напряжением. Поэтому можно предположить, что сила тока зависит от напряжения. Установим, какова эта зависимость, на опыте.

На рисунке изображена электрическая цепь, состоящая из источника тока — аккумулятора, амперметра, спирали из никелиновой проволоки, ключа и параллельно присоединенного к спирали вольтметра. Замыкают цепь и отмечают показания приборов. Затем присоединяют к первому аккумулятору второй такой же аккумулятор и снова замыкают цепь. Напряжение на спирали при этом увеличится вдвое, и амперметр покажет вдвое большую силу тока. При трех аккумуляторах напряжение на спирали увеличивается втрое, во столько , же раз увеличивается сила тока. Таким образом, опыт показывает, что во сколько раз увеличивается напряжение, приложенное к одному и тому же проводнику, во столько же раз увеличивается сила тока в нем. Другими словами, сила тока в проводнике прямо пропорциональна напряжению на концах проводника. На рисунке показан график зависимости силы тока в проводнике от напряжения между концами этого проводника. На графике в условно выбранном масштабе по горизонтальной оси отложено напряжение в вольтах, а по вертикальной — сила тока в амперах.

Зависимость силы тока от напряжения мы уже установили. На основании опытов было показано, что сила тока в проводнике прямо пропорциональна напряжению на концах проводника

Следует обратить внимание, что при проведении опыта сопротивление проводника не менялось, одна и та же спираль служила участком цепи, на котором измеряли напряжение и силу тока. При проведении физических опытов, в которых определяют зависимость одной величины от другой, все остальные величины должны быть постоянными, если они будут изменяться, то установить зависимость будет сложнее

Поэтому, определяя зависимость силы тока от сопротивления, напряжение на концах проводника надо поддерживать постоянным. Чтобы ответить на вопрос, как зависит сила тока в цепи от сопротивления, обратимся к опыту. На рисунке изображена электрическая цепь, источником тока в которой является аккумулятор. В эту цепь по очереди включают проводники, обладающие различными сопротивлениями. Напряжение на концах проводника во время опыта поддерживается постоянным. За этим следят по показаниям вольтметра. Силу тока в цепи измеряют амперметром. Ниже в таблице приведены результаты опытов с тремя различными проводниками: В первом опыте сопротивление проводника 1 Ом и сила тока в цепи 2 А. Сопротивление второго проводника 2 Ом, т.е. в два раза больше, а сила тока в два раза меньше. И наконец, в третьем случае сопротивление цепи увеличилось в четыре раза и во столько же раз уменьшилась сила тока. Напомним, что напряжение на концах проводников во всех трех опытах было одинаковое, равное 2 В. Обобщая результаты опытов, приходим к выводу: сила тока в проводнике обратно пропорциональна сопротивлению проводника.

Зависимость силы тока от напряжения на концах участка цепи и сопротивления этого участка называется законом Ома по имени немецкого ученого Ома, открывшего этот закон в 1827 г. Закон Ома читается так: сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению: I=U/R здесь I — сила тока в участке цепи, U — напряжение на этом участке, R — сопротивление участка.Закон Ома — один из основных физических законов. На рисунке зависимость силы тока от сопротивления проводника при одном и том же напряжении на его концах показана графически. На этом графике по горизонтальной оси в условно выбранном масштабе отложены сопротивления проводников в омах, по вертикальной — сила тока в амперах. Из формулы I=U/R — следует, что U=IR и R=U/I . Следовательно, зная силу тока и сопротивление, можно по закону Ома вычислить напряжение на участке цепи, а зная напряжение и силу тока — сопротивление участка. Сопротивление проводника можно определить по формуле R=U/I , однако надо понимать, что R — величина постоянная для данного проводника и не зависит ни от напряжения, ни от силы тока. Если напряжение на данном проводнике увеличится, например, в 3 раза, то во столько же раз увеличится и сила тока в нем, а отношение напряжения к силе тока не изменится.

Источник

4 вариант

1. Ток в электронагревательном приборе 5 А. Чему равен заряд, который пройдет через нагреватель за 3 минуты?

1) 15 Кл
2) 36 Кл
3) 900 Кл
4) 3600 Кл

2. На рисунке изображён график зависимости силы тока в проводнике от на­пряжения на его концах. Чему равно сопротивление проводника?

1) 0,125 Ом
2) 2 Ом
3) 16 Ом
4) 8 Ом

3. Если напряжение между концами проводника и его длину уменьшить в 2 раза, то сила тока, протекающего через проводник,

1) уменьшится в 2 раза
2) не изменится
3) увеличится в 2 раза
4) уменьшится в 4 раза

4. Рассчитайте общее сопротив­ление участка цепи, изобра­жённого на рисунке, если со­противление каждого элемента цепи равно 1 Ом.

1) 3 Ом
2) 2 Ом
3) 1,5 Ом
4) 1/3 Ом

5. При силе тока 0,6 А сопротивление лампы равно 5 Ом. Определите мощность электрического тока лампы.

1) 0,06 Вт
2) 1,8 Вт
3) 3 Вт
4) 15 Вт

6. Чему равно напряжение на концах проводника, если при прохождении по нему электрического тока 4 А в течение 7,5 минут выделяется 216 кДж теплоты?

1) 0,12 В
2) 7,2 В
3) 120 В
4) 7200 В

7. Установите соответствие между физическими величи­нами и единицами измерения этих величин.
К каждой позиции первого столбца подберите соответ­ствующую позицию второго.

Физическая величина

А) Сила тока
Б) Напряжение
В) Мощность

Единицы измерения

1) Джоуль
2) Ампер
3) Вольт
4) Ватт
5) Ом

8. Троллейбус движется равномерно по горизонтальному участку пути со скоростью 36 км/ч. Сила сопротивле­ния, действующая на троллейбус, равна 2,2 кН. Найди­те силу тока в обмотке двигателя, если напряжение на клеммах двигателя 550 В, а КПД равен 80% .

Ответы на контрольную работу по физике Постоянный ток1 вариант
1-2
2-1
3-3
4-3
5-1
6-4
7-513
8. ≈ 5,73 А2 вариант
1-4
2-4
3-3
4-3
5-2
6-1
7-451
8. 50%3 вариант
1-1
2-4
3-2
4-4
5-2
6-2
7-431
8. ≈ 3,73 А4 вариант
1-3
2-4
3-2
4-3
5-2
6-3
7-234
8. 50 А

Электрическая цепь и закон Ома

Три величины — напряжение, электрический ток и сопротивление — могут быть четко представлены в электрической цепи. В простейшем случае она состоит из источника постоянного напряжения и резистора. Резистор подключен к источнику напряжения, а для упрощения возьмем, что сопротивление проводов равно 0 Ом.

Электрическая цепь

Направление электрического тока.

В электротехнике ток течет от плюса до минуса (смотрите рисунок ). Другими словами, как только возникает замкнутая цепь, ток начинает течь от положительного полюса к отрицательному полюсу источника напряжения. Мы говорим о замкнутой цепи, когда два полюса источника напряжения соединены друг с другом сопротивлением.

Как и чем измерять ток и напряжение?

Есть два способа определения силы тока и напряжения. С одной стороны, их можно определить арифметически с помощью закона Ома для участка цепи. С другой стороны, две переменные также могут быть определены путем измерения.

Однако для арифметического определения тока или напряжения должны быть известны две другие величины (напряжение и сопротивление либо ток и сопротивление).

С другой стороны, метрологический метод также работает с любой электрической цепью. Для этого в электрическую цепь необходимо вставить амперметр и вольтметр . Они используются для измерения силы тока и напряжения. Но здесь также применяется закон Ома, поскольку сопротивление нельзя измерить напрямую, но его можно будет рассчитать, когда будут измерены значения тока и напряжения.

Итак, ток измеряется так амперметром, который последовательно подключается к потребителю (резистору, лампе накаливания и т. д.), Через который нужно определять ток. На принципиальной схеме он изображен как A внутри круга (см. рисунок 1). Амперметр имеет очень низкое внутреннее сопротивление, чтобы не влиять на ток, который должен протекать через потребителя. В идеале, внутреннее сопротивление амперметра принимается равным 0 Ом и поэтому просто опускается.

Измерение напряжения производится с помощью вольтметра, который замеряет разность потенциалов между двумя его точками подключения. На электрической схеме он обозначен буквой V внутри круга (см. рисунок 1). В отличие от амперметра, вольтметр подключается параллельно нагрузке, на которой измеряется напряжение. Добавление вольтметра параллельно некоторому потребителю (например, резистору) создает току еще один «обходной» путь, что резко изменяет параметры цепи. Чтобы избежать этих нежелательных последствий, надо применять вольтметры с максимально большим сопротивлением.

Вольт-амперная характеристика (ВАХ).

Вольт-амперная характеристика или характеристика UI резистора может быть записана путем приложения к нему различных напряжений и последующего измерения тока. Обычно при омическом сопротивлении достаточно одной точки измерения, которая затем соединяется с началом системы координат. Однако на практике, для целей контроля, выполняют серию измерений с тремя точками измерения.

Затем эти точки измерения отмечаются в системе координат и соединяются. Напряжение откладывают по оси абсцисс, а ток — по оси ординат. Пример ВАХ смотрите на рисунке ниже

Вольт-амперная характеристика

ВАХ может быть использована для определения тока через резистор при определенном напряжении.

Предыдущая
РазноеЭнергия конденсатора
Следующая
РазноеАвтоматические выключатели

2 вариант

1. Сила тока, идущего по проводнику, равна 2 А. Какой заряд проходит по проводнику за 10 минут?

1) 0,2 Кл
2) 5 Кл
3) 20 Кл
4) 1200 Кл

2. При увеличении напряжения U на участке электрической цепи сила тока I в цепи изменяется в соответ­ствии с графиком (см. рисунок). Электрическое сопротивление на этом участке цепи равно

1) 2 Ом
2) 0,5 Ом
3) 2 мОм
4) 500 Ом

3. Если увеличить в 2 раза напряжение между концами проводника, а его длину уменьшить в 2 раза, то сила тока, протекающего через проводник,

1) не изменится
2) уменьшится в 4 раза
3) увеличится в 4 раза
4) увеличится в 2 раза

4. Сопротивление участка цепи, изображённого на рисунке, равно

1) 11 Ом
2) 6 Ом
3) 4 Ом
4) 1 Ом

5. На цоколе лампы накаливания написано: «150 Вт, 220 В». Найдите силу тока в спирали при включении в сеть с номинальным напряжением

1) 0,45 А
2) 0,68 А
3) 22 А
4) 220000 А

6. Проволочная спираль, сопротивление которой в нагре­том состоянии равно 55 Ом, включена в сеть с напря­жением 127 В. Какое количество теплоты выделяет эта спираль за 1 минуту?

1) 17,595 кДж
2) 20 кДж
3) 230 кДж
4) 658,5 кДж

7. Установите соответствие между физическими величи­нами и единицами измерения этих величин.
К каждой позиции первого столбца подберите соответ­ствующую позицию второго.

Физическая величина

А) Сила тока
Б) Сопротивление
В) Работа электрического тока

Единицы измерения

1) Джоуль
2) Ватт
3) Вольт
4) Ампер
5) Ом

8. Электродвигатель подъёмного крана подключён к ис­точнику тока напряжением 380 В, при этом сила тока в обмотке 20 А. Определите КПД подъёмного крана, если он поднимает груз массой 1 т на высоту 19 м за 50 с.

Задача на соединение конденсаторов, параллельное и последовательное

Условие. Имеются три конденсатора с емкостями 20, 25 и 30 мкФ. Определите их общую емкость при последовательном и параллельном соединении.

Решение. Проще начать с параллельного подключения. В этой ситуации все три значения нужно просто сложить. Таким образом, общая емкость оказывается равной 75 мкФ.

Несколько сложнее расчеты будут при последовательном соединении этих конденсаторов. Ведь сначала нужно найти отношения единицы к каждой из этих емкостей, а потом сложить их друг с другом. Получается, что единица, деленная на общую емкость, равна 37/300. Тогда искомая величина получается приблизительно 8 мкФ.

Ответ. Общая емкость при последовательном соединении 8 мкФ, при параллельном — 75 мкФ.

Проводники в электрических цепях могут соединяться последовательно и параллельно.

При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:

.

Рисунок 1.9.1.

По закону Ома, напряжения и на проводниках равны

.

Общее напряжение на обоих проводниках равно сумме напряжений ₁ и ₂:

,

где – электрическое сопротивление всей цепи. Отсюда следует:

= 1 + 2.

При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Этот результат справедлив для любого числа последовательно соединенных проводников.

При параллельном соединении (рис. 1.9.2) напряжения ₁ и ₂ на обоих проводниках одинаковы:

.

Сумма токов ₁ + ₂, протекающих по обоим проводникам, равна току в неразветвленной цепи:

= 1 + 2.

Этот результат следует из того, что в точках разветвления токов (узлы и ) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу за время Δ подтекает заряд Δ, а утекает от узла за то же время заряд ₁Δ + ₂Δ. Следовательно, = ₁ + ₂.

Рисунок 1.9.2.

Записывая на основании закона Ома

где – электрическое сопротивление всей цепи, получим

При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Этот результат справедлив для любого числа параллельно включенных проводников.

Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.

Рисунок 1.9.3.

Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.

Рисунок 1.9.4.

Цепи, подобные изображенной на рис. 1.9.4, а также цепи с разветвлениями, содержащие несколько источников, рассчитываются с помощью правил Кирхгофа.

Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением. Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при паралл ельном и последовательном соединении резисторов будет различной. Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.

Закон Ома

Экспериментально доказано, что во сколько раз увеличивается напряжение на участке цепи, во столько же раз увеличивается и сила тока на этом участке. То есть сила тока в проводнике прямо пропорциональна напряжению на концах этого проводника.

График зависимости силы тока от напряжения будет представлять собой прямую линию, проходящую через начало координат . Его называют вольт-амперной характеристикой цепи.

Зависимость силы тока от сопротивления  показывает, что чем больше сопротивление проводника, тем меньше сила тока при одном и том же напряжении между концами проводника. Поэтому сила тока в проводнике обратно пропорциональна сопротивлению проводника

Для участка цепи величина I рассчитывается по формуле немецкого физика Георга Ома, открывшего в 1926 г. закон взаимосвязи между силой тока, напряжением и сопротивлением проводника:

I=U/R,

• U – напряжение (или падение напряжения, или разность потенциалов), измеряется в вольтах – обозначение В или V;
• R – сопротивление проводника, измеряется в омах – обозначение Ом или W.

Или по формуле I=UG, где обозначение G – это проводимость или электропроводность (величина, обратная сопротивлению, измеряется в сименсах, обозначение – См или S).

Расчет для полной цепи происходит по формуле I=e/R+r, где:

• e – ЭДС или электро-движущая сила в цепи, измеряется в вольтах;
• R – суммарное сопротивление всех приборов, включенных в цепь;
• r – внутреннее сопротивление источника напряжения.

Сила тока зависит от электрического напряжения (или разности потенциалов, или ЭДС). В случаях, когда r<>R, можно считать, что она обратно пропорциональна либо сопротивлению цепи, либо сопротивлению источника.

Закон Ома для полной цепи.

Значение I связано с показателем скорости преобразования электрической энергии – мощностью P (единицы измерения ватты -обозначение Вт или W). Для линейной цепи, в которой соблюдается закон Ома, расчет P производится по формуле:

P=IU или P=I2R=U2/R.

Общее сопротивление электрической цепи, чему оно равно и как найти по формуле.

Как известно во всем нужна своя мера, которая позволяет делать точные системы, устройства, механизмы, схемы. Мера множественная, имеет свои конкретные величины. В сфере электротехники основными величинами являются напряжение, ток, сопротивление, мощность, частота (для переменного и импульсного тока). Величины между собой связаны определенными формулами

Самой важной формулой, наиболее используемой электриками, электронщиками является закон Ома ( I = U/R, то есть — сила тока равна напряжению деленному на сопротивление). Зная любые две величины из этой формулы всегда можно найти третью

От сопротивления электрической цепи зависит силы тока при наличии определенного напряжения. Если меняется сопротивление в цепях схемы, то и меняться режимы ее работы в отдельных ее участках или во всей цепи. Знание величины сопротивления могут помочь выявить неисправность, узнать (вычислить из формулы) другие электрические величины в схеме, зависящие от этого сопротивления.

Теперь давайте посмотрим от чего зависит общее сопротивление электрической цепи. Общее — это сумма частных. Любая электрическая цепь и схема содержит в себе электрические компоненты, которые обладают внутренним сопротивлением. Даже обычный конденсатор (две пластины проводника, разделенные диэлектриком, что позволяет накапливать электрический заряд между этими пластинами, не пропуская постоянный ток), который, казалось бы, по сути своей его не должен иметь (точнее оно бесконечно большое) обладает реактивным сопротивлением.

Самая простая электрическая цепь состоит из источника питания и нагрузки. К примеру это будет обычная батарейка и маленькая лампочка накаливания. И батарейка и лампочка имеют свои сопротивления, которые суммируются, что определяет силу тока, текущему по этой простейшей цепи (при определенной величине напряжения). Допустим к нашей цепи мы добавим еще один элемент нагрузки (вторую такую же лампочку). Ее можно подключить к этой простейшей цепи двумя способами либо параллельно первой лампочки, либо же последовательно ей

При последовательном подключении сопротивление будет суммироваться:

При параллельном подключении общее сопротивление можно найти по таким формулам:

То есть, большинство схем будут иметь в себе либо параллельное подключение сопротивлений, либо последовательное или же смешанное. В случае сложной электрической цепи определение общего электрического сопротивления происходит по частям (группам), состоящим, опять же, из параллельных и последовательных подключений элементов, обладающими сопротивлением. Правильнее начинать с той части цепи, схемы, которая имеет наибольшую удаленность от двух конечных выводов, рассматриваемых как контакты общего сопротивления. На рисунке ниже приведен пример последовательности вычисления общего сопротивления сложной цепи, схемы.

Но ведь существуют электрические цепи, в которых общее сопротивление может постоянно меняться, к примеру схема стабилизированного регулятора частоты вращения постоянного электродвигателя, подключенная к самому двигателю. При изменении нагрузки на валу двигателя будет меняться его внутреннее сопротивление, следовательно меняться будет и режимы работы схемы (поддерживающая нужную частоту вращения вала). В таких цепях электрическое сопротивление является динамическим, изменяющемся. Можно лишь рассчитать усредненное сопротивление, которое не будет абсолютно точным.

Помимо этого, как было подмечено ранее, существует еще реактивное сопротивление, которое бывает у индуктивных и емкостных элементов цепи. Оно явно себя проявляет в схемах, что работают с переменным, импульсным током. Если в цепях постоянного тока конденсатор (стоящий последовательно) не будет проводить через себя ток, то в цепи переменного тока будет все иначе. Причем его реактивное сопротивление будет зависеть от частоты (при одной и той же емкости). Вот формулы для нахождения реактивного емкостного и индуктивного сопротивления:

P.S. общее сопротивление можно находить и через использование закона Ома, который гласит, что сопротивление равно напряжение деленное на силу тока. Следовательно, берем мультиметр, измеряем ток и напряжение в том месте цепи, где хотим узнать сопротивление. Воспользовавшись формулой Ома находим (определяем) электрическое сопротивление нужного участка цепи. Напомню, что при использовании закона ома нужно применять основные единицы измерения — ток в амперах, напряжение в вольтах, а сопротивление в омах.

Закон Ома для участка цепи

С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.

Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. В результате этих реакций выделяется энергия, которая потом передается электрической цепи.

У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «−».

У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.

Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.

Математически его можно описать вот так:

Закон Ома для участка цепи I = U/R I — сила тока U — напряжение R — сопротивление

Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.

Сила тока измеряется в амперах, а подробнее о ней вы можете прочитать в нашей статье.

Давайте решим несколько задач на закон Ома для участка цепи.

Задача раз

Найти силу тока в лампочке накаливания торшера, если его включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом.

Решение:

Возьмем закон Ома для участка цепи:

I = U/R

Подставим значения:

I = 220/880 = 0,25 А

Ответ: сила тока, проходящего через лампочку, равна 0,25 А

Давайте усложним задачу. И найдем силу тока, зная все параметры для вычисления сопротивления и напряжение.

Задача два

Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а длина нити накаливания равна 0,5 м, площадь поперечного сечения 0,01 мм2, а удельное сопротивление нити равно 1,05 Ом · мм2/м.

Решение:

Сначала найдем сопротивление проводника.

R = ρ · l/S

Площадь дана в мм2, а удельное сопротивления тоже содержит мм2 в размерности.

Это значит, что все величины уже даны в СИ и перевод не требуется:

R = 1,05 · 0,5/0,01 = 52,5 Ом

Теперь возьмем закон Ома для участка цепи:

I = U/R

Подставим значения:

I = 220/52,5 ≃ 4,2 А

Ответ: сила тока, проходящего через лампочку, приблизительно равна 4,2 А

А теперь совсем усложним! Определим материал, из которого изготовлена нить накаливания.

Задача три

Из какого материала изготовлена нить накаливания лампочки, если настольная лампа включена в сеть напряжением 220 В, длина нити равна 0,5 м, площадь ее поперечного сечения равна 0,01 мм2, а сила тока в цепи — 8,8 А

Решение:

Возьмем закон Ома для участка цепи и выразим из него сопротивление:

I = U/R

R = U/I

Подставим значения и найдем сопротивление нити:

R = 220/8,8 = 25 Ом

Теперь возьмем формулу сопротивления и выразим из нее удельное сопротивление материала:

R = ρ · l/S

ρ = RS/l

Подставим значения и получим:

ρ = 25 · 0,01/0,5 = 0,5 Ом · мм2/м

Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.

Ответ: нить накаливания сделана из константана.