Контрольная по электротехнике электрические цепи переменного тока

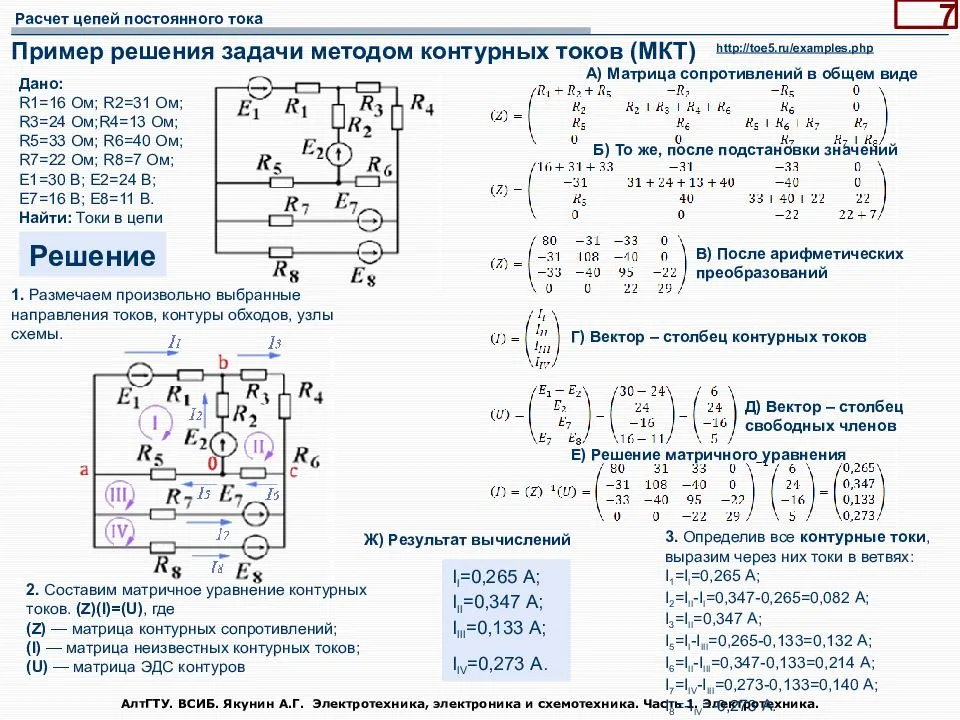
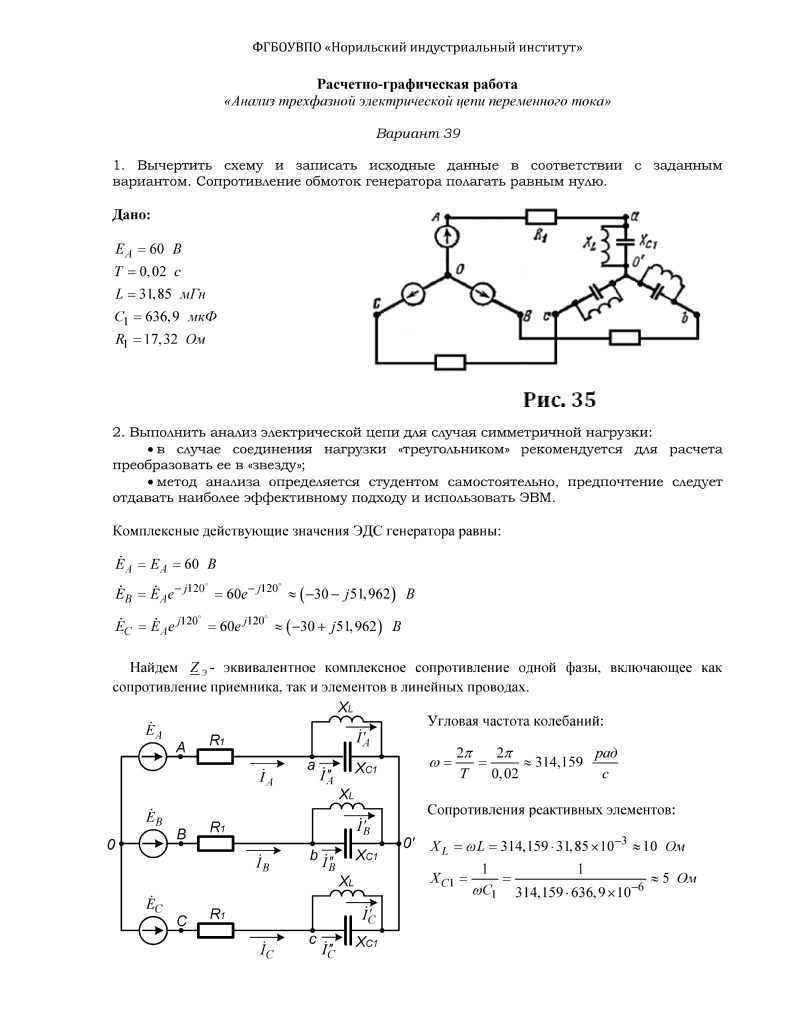
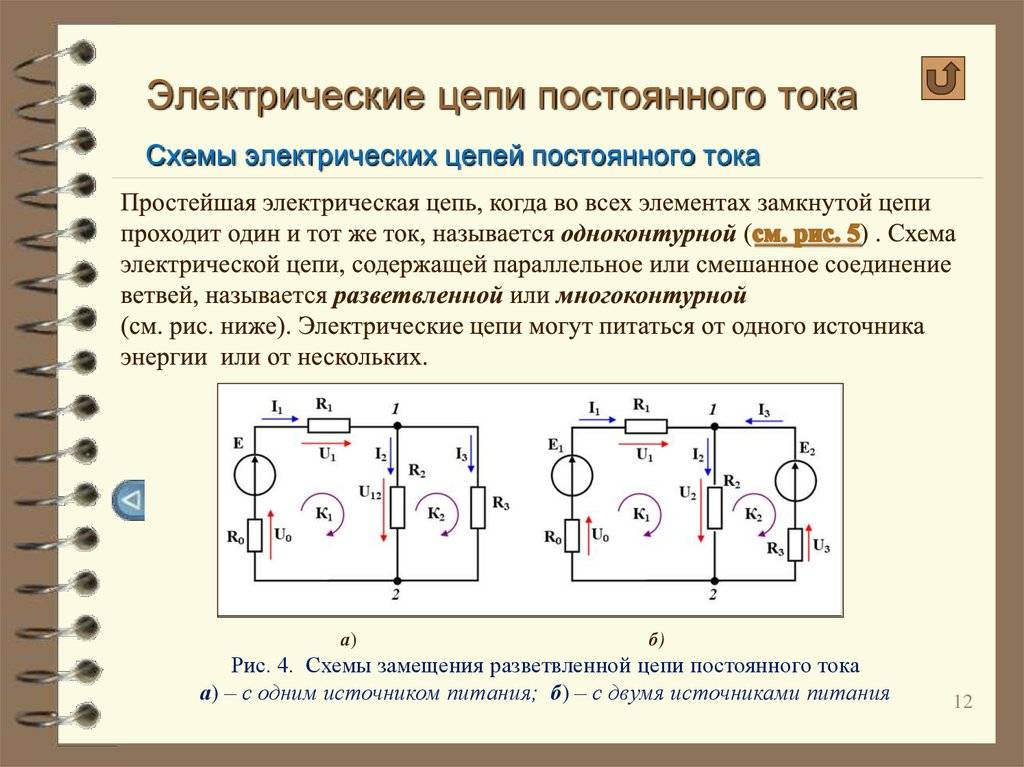
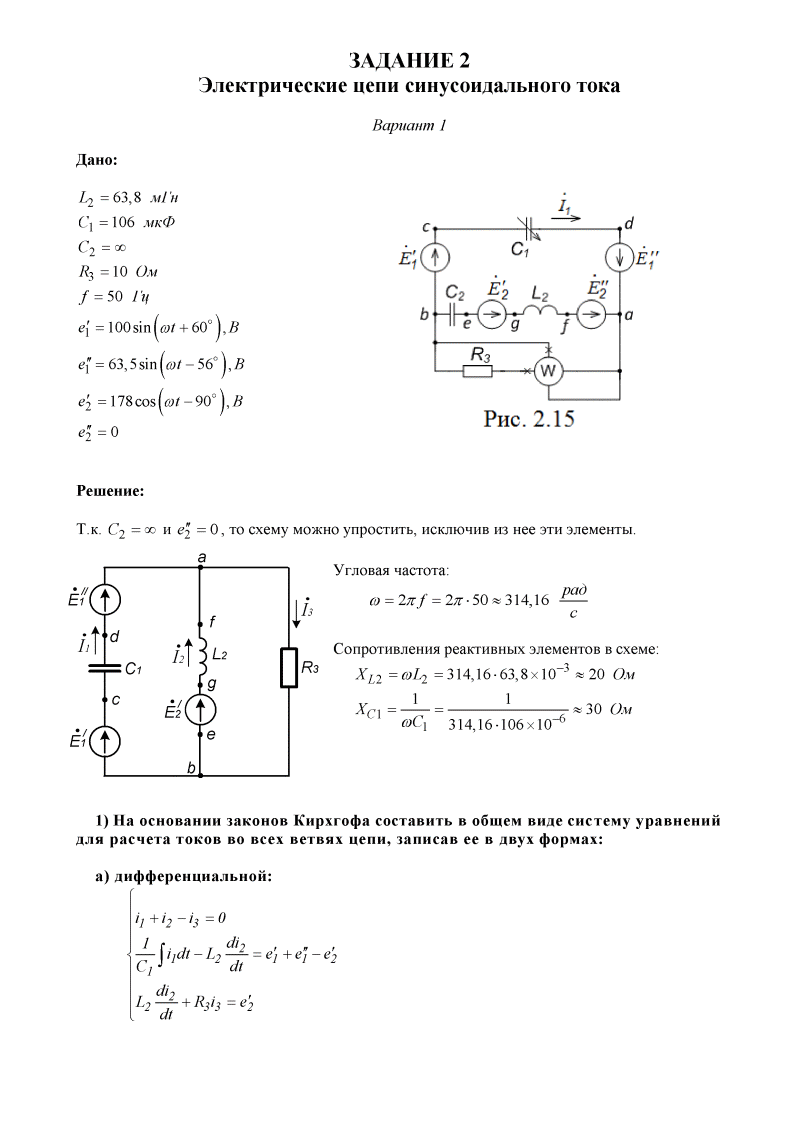
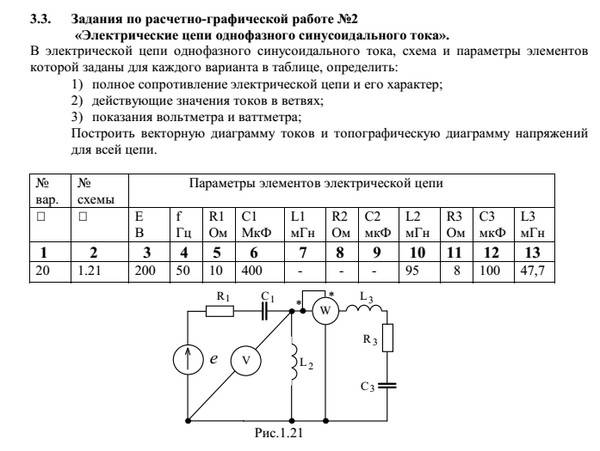
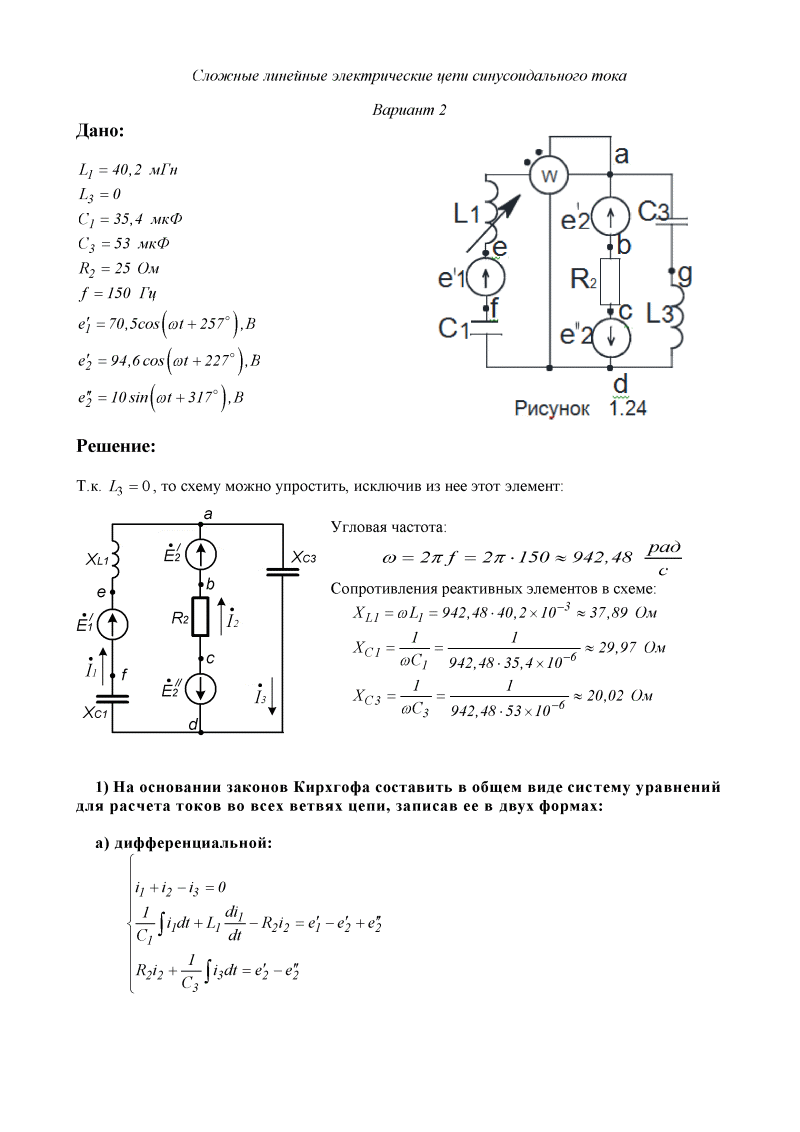
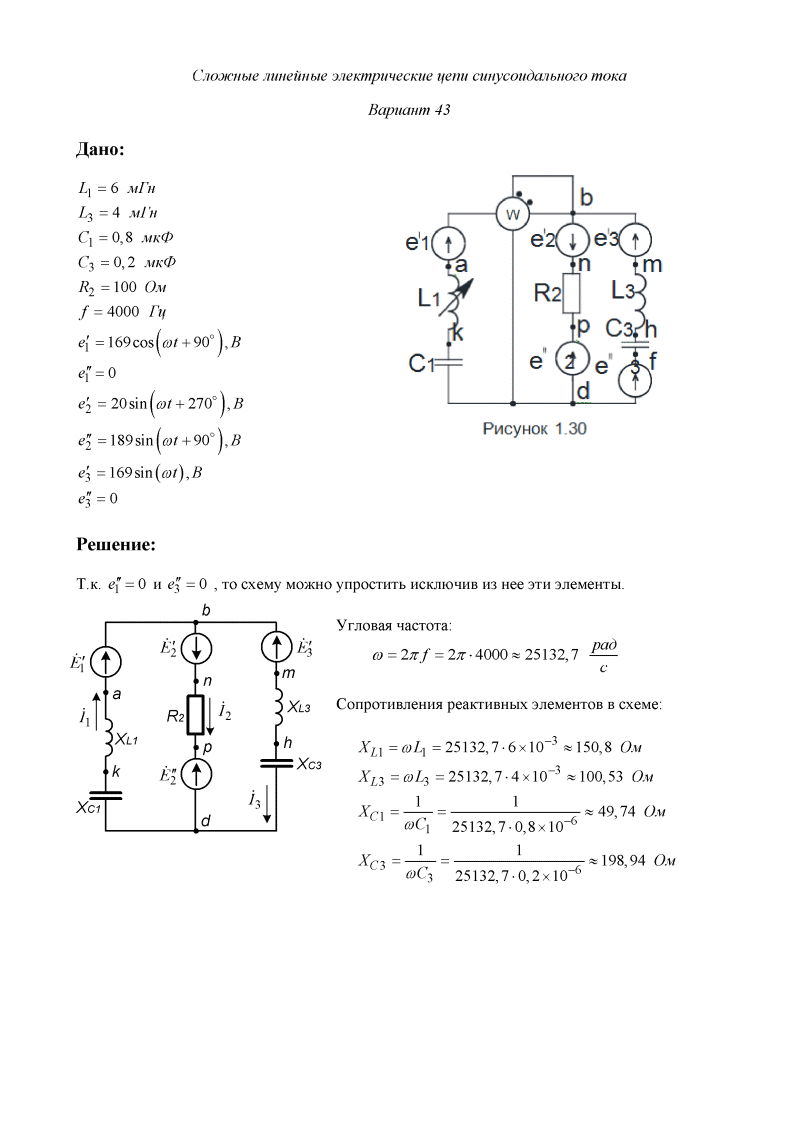
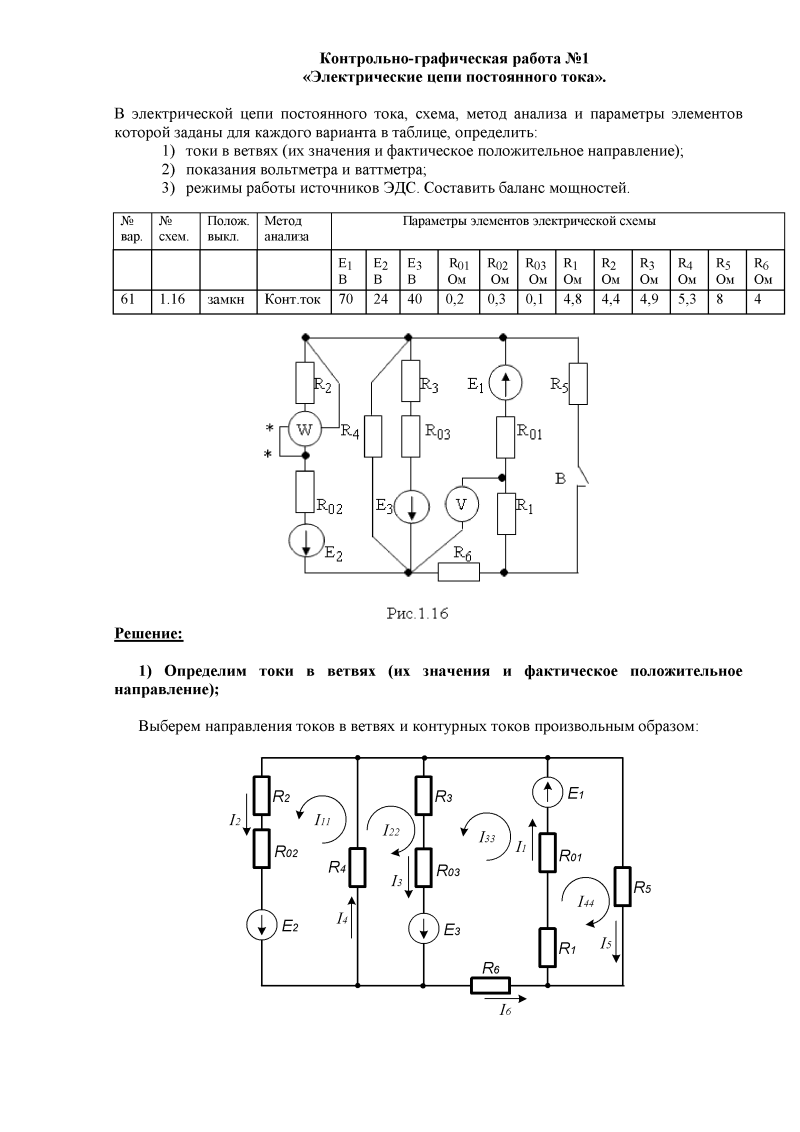
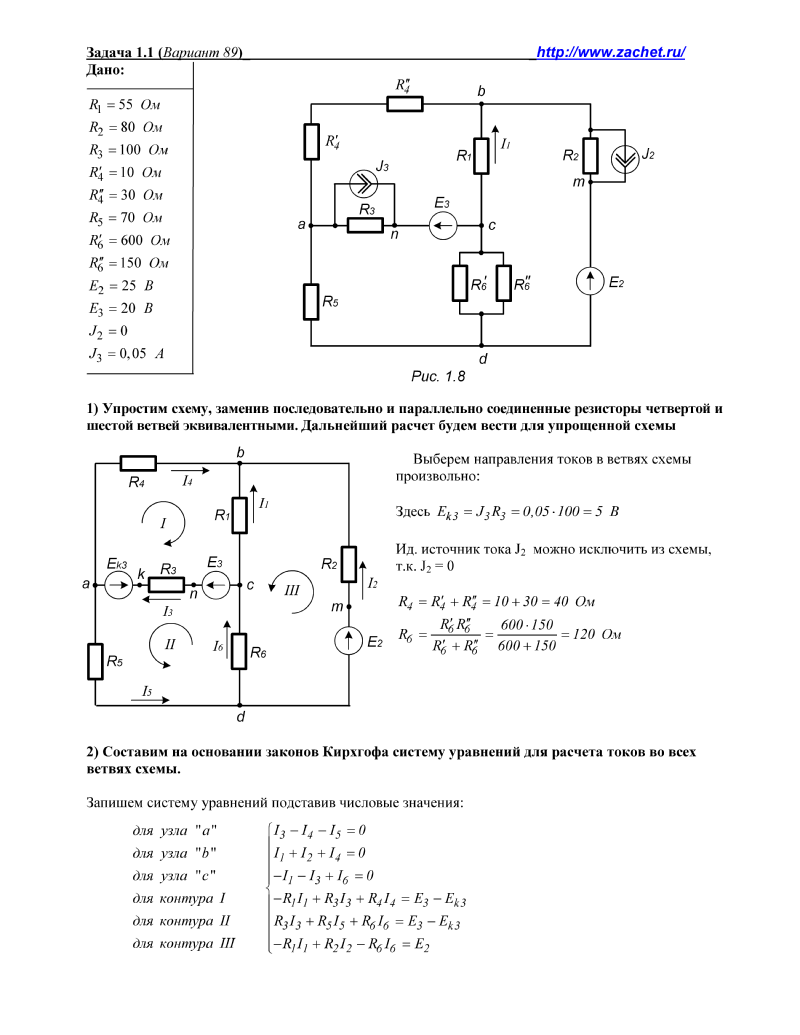
Мощность при переменном токе

Предположим, что имеется потребитель электрической энергии (рис. 1.9.), напряжение и ток которого известны

u= Um sin(ωt+ψu), i= Im sin ωt

Рис. 1.9. Схема и векторная диаграмма потребителя

На рис. 1.9,б

приведена векторная диаграмма потребителя. В зависимости от характера нагрузки, т.е. характера сопротивлений потребителя, угол сдвига фаз между напряжением и током

φ = ψu – ψi

может лежать в пределах от π/2 до –π/2. В рассматриваемом случае φ=ψu так как ψi=0.

При переменном токе различают следующие мощности: мгновенную, активную, реактивную и полную (кажущуюся).

Под мгновенной понимается мощность, равная произведению мгновенных значений напряжения и тока:

P=u·i

С течением времени мгновенная мощность изменяется как по величине, так и по знаку.

При активной нагрузке (рис. 1.10,а, φ=0) в течение всего периода изменения тока мгновенная мощность положительна. В этом случае электрическая энергия забирается из сети и обратно в сеть не возвращается. Она преобразуется в тепло, в механическую энергию и т.д.

При индуктивной нагрузке (рис. 1.10,а, φ=π/2) в одну четверть периода изменения тока мгновенная мощность положительна, в другую – отрицательна. Соответственно, в одну четверть периода электрическая энергия забирается из сети и преобразуется в энергию магнитного поля, в другую – такое же количество энергии преобразуется из энергии магнитного поля, в электрическую энергию и возвращается в сеть.

В случае емкостной нагрузки (рис. 1.10,в, φ= — π/2) в одну четверть периода электрическая энергия забирается из сети и преобразуется в энергию электрического поля, в другую – энергия электрического поля преобразуется в электрическую энергию и возвращается в сеть.

В случае смешанной активно-индуктивной (0<�φ<�π/2) или активно-емкостной нагрузки (0<�φ< — π/2) забираемая из сети электрическая энергия больше энергии, возвращаемой в сеть. В сеть возвращается только та часть энергии, которая была преобразована в энергию магнитного или электрического поля.

Рис. 1.10. Графики тока, напряжения и мощности при различных нагрузках

Под активной понимается мощность, равная среднему значению мгновенной мощности за период

Если разложить ток потребителя на составляющие (рис. 1.9, б), то получим

где — активная составляющая тока

где — реактивная составляющая тока

Активную мощность можно выразить следующим образом

Активная мощность обусловлена совпадающими по фазе напряжением и током. Входящий в выражение мощности cosφ получил название коэффициент мощности. Чем больше cosφ потребителя, тем больше будет при неизменных токе и напряжении активная составляющая тока и активная мощность. Когда φ = π/2 или φ = — π/2 (рис. 1.10,б,в) cosφ и активная мощность равна нулю.

Реактивная мощность (индуктивная или емкостная) выражается следующим образом

Q=U·I·sin φ

Реактивная мощность обусловлена током и напряжением, сдвинутым по фазе на угол φ=±π/2.

Реактивная мощность соответствует энергии, которая в одну четверть периода забирается из сети и преобразуется потребителем в энергию магнитного или электрического поля, а в другую – вновь преобразуется в электрическую энергию и возвращается в сеть.

Полная (кажущаяся) мощность включает в себя активную и реактивную мощности и равна

S=U·I

Между активной, реактивной и полной мощностями существуют соотношения

Все перечисленные мощности имеют одну и ту же размерность:

вольт х ампер (В·А). Однако, для того, чтобы различать эти мощности, единицы их измерения называют по-разному:

ед. P = 1 Вт – ватт;

ед. Q = 1 ВАр – вольтампер реактивный;

ед. S = 1 ВА – вольтампер.

Как найти активную, реактивную и полную мощность

Активная мощность относится к энергии, которая необратимо расходуется источником за единицу времени для выполнения потребителем какой-либо полезной работы. В процессе потребления, как уже было отмечено, она преобразуется в другие виды энергии.

В цепи переменного тока значение активной мощности определяется, как средний показатель мгновенной мощности за установленный период времени. Следовательно, среднее значение за этот период будет зависеть от угла сдвига фаз между током и напряжением и не будет равной нулю, при условии присутствия на данном участке цепи активного сопротивления. Последний фактор и определяет название активной мощности. Именно через активное сопротивление электроэнергия необратимо преобразуется в другие виды энергии.

При выполнении расчетов электрических цепей широко используется понятие реактивной мощности. С ее участием происходят такие процессы, как обмен энергией между источниками и реактивными элементами цепи. Данный параметр численно будет равен амплитуде, которой обладает переменная составляющая мгновенной мощности цепи.

Существует определенная зависимость реактивной мощности от знака угла ф, отображенного на рисунке. В связи с этим, она будет иметь положительное или отрицательное значение. В отличие от активной мощности, измеряемой в ваттах, реактивная мощность измеряется в вар – вольт-амперах реактивных. Итоговое значение реактивной мощности в разветвленных электрических цепях представляет собой алгебраическую сумму таких же мощностей у каждого элемента цепи с учетом их индивидуальных характеристик.

Основной составляющей полной мощности является максимально возможная активная мощность при заранее известных токе и напряжении. При этом, cosф равен 1, когда отсутствует сдвиг фаз между током и напряжением. В состав полной мощности входит и реактивная составляющая, что хорошо видно из формулы, представленной выше. Единицей измерения данного параметра служит вольт-ампер (ВА).

Пусть приемник электро­энергии присоединен к источнику синусоидального напряжения u(t) = Usin(ωt) и потребляет синусоидальный ток i(t) = I sin (ωt -φ), сдви­нутый по фазе относительно напряжения на угол φ. U и I – действующие значения. Значение мгновенной мощности на зажимах приемника определяется выражением

p(t) = u(t) ?i(t) = 2UI sin(ωt) sin (ωt -φ) = UI cos φ — UI cos (2ωt -φ)

(5.1)

и является суммой двух величин, одна из которых постоянна во времени, а другая пульсирует с двойной частотой.

Среднее значение p(t) за период Т называется активной мощностью и полностью определяется первым слагаемым уравнения (5.1):

Активная мощность ха­рактеризует энергию, расходуемую необратимо источником в единицу времени на производство полезной работы потребителем. Активная энергия, потребляемая электроприёмниками, преобразуется в другие виды энергии: механическую, тепловую, энергию сжатого воздуха и газа и т. п.

Кривые напряжения и тока в емкостном сопротивлении

В идеальной емкости ток опережает напряжение на 90°

Режим – состояние электрической цепи переменного тока описывается дифференциальными уравнениями, представляющими собой уравнения с постоянными коэффициентами и правой частью, например:

Из курса высшей математики известно, что общее решение такого уравнения может быть найдено методом наложения принужденного и свободного режимов:

где

– ток принужденного режима при di/dt=0

– ток свободного режима.

Свободные процессы исследуются с целью определения устойчивости системы. В устойчивой системе процессы должны затухать. Принужденный и свободный режимы в сумме определяют процессы, которые называются переходными, т.е. осуществляется переход от одного установившегося режима к другому.

При установившемся режиме ток и напряжение сохраняют в течение длительного времени амплитудные значения.

В цепях постоянного тока токи и напряжения остаются неизменными, а в цепях переменного тока остаются неизменными кривые изменения токов и напряжений.

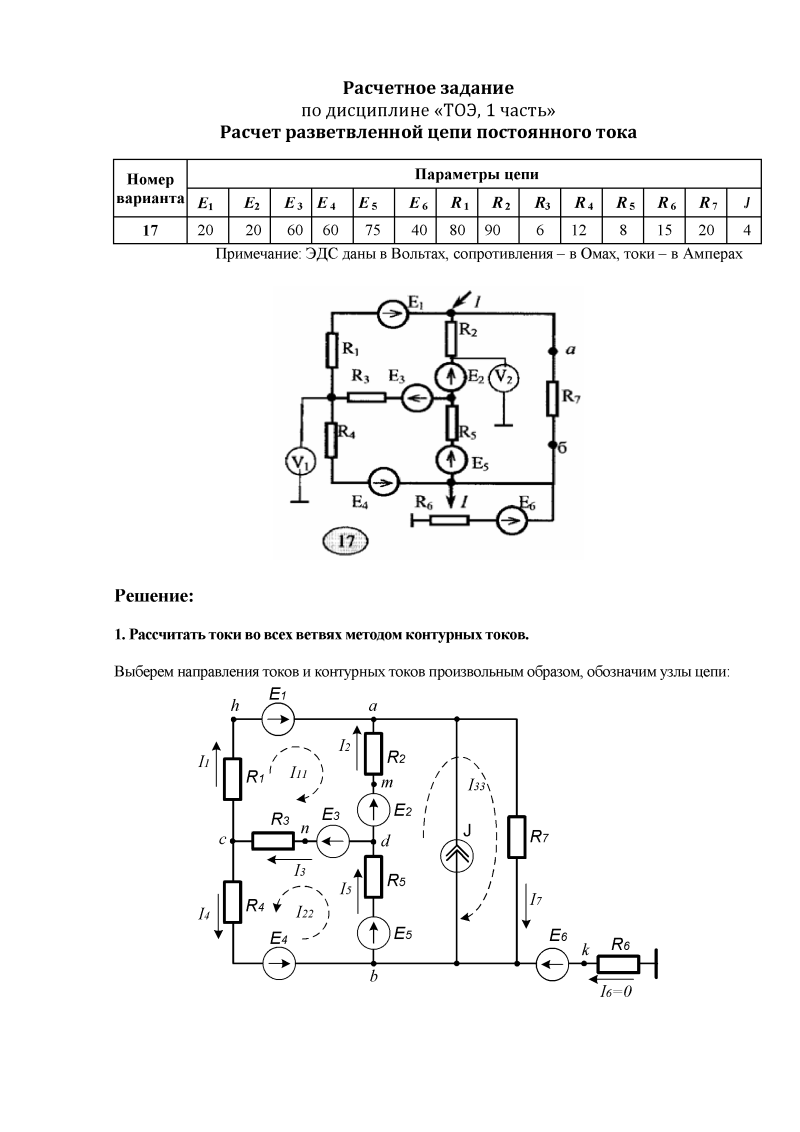
АГЗ МЧС РГР №1 Расчёт линейных цепей постоянного тока

Задание 1 Расчёт линейных цепей постоянного тока

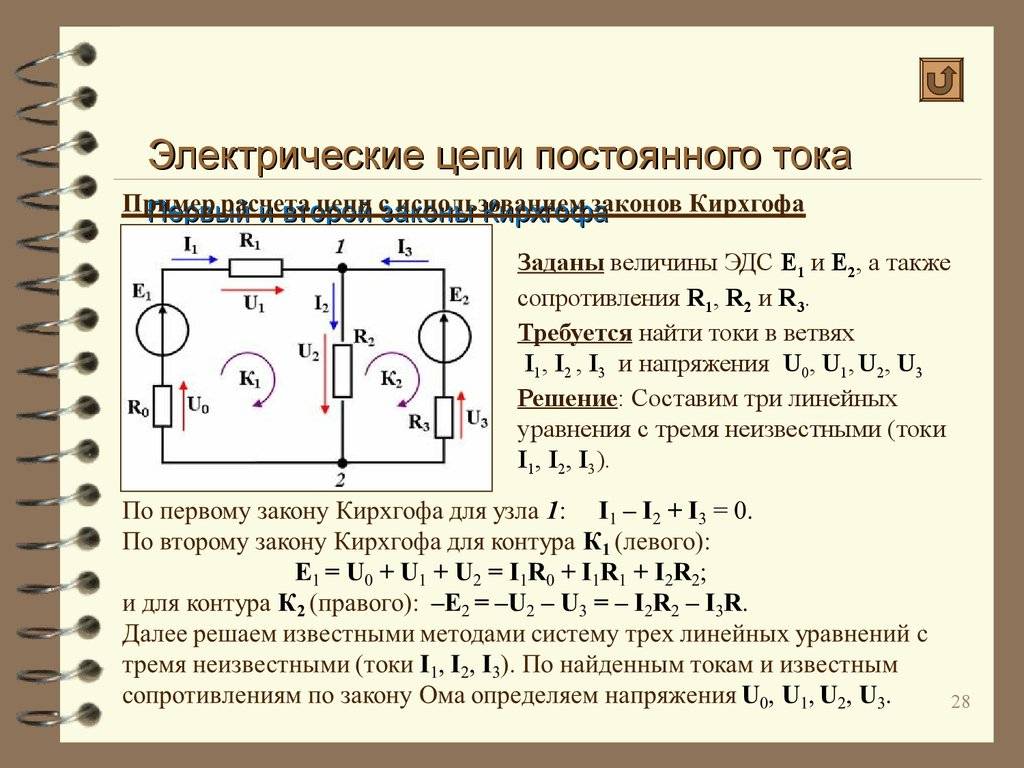
Для электрической схемы, изображенной на рисунках 1.1 – 1.50, по заданным в таблице 1.2 сопротивлением и ЭДС выполнить следующее:

1. Составить систему уравнений, необходимых для определения токов по первому и второму правилам Кирхгофа.
2. Найти и вычислить все токи, пользуясь методом контурных токов (решения провести с помощью составления матрицы для системы уравнений и определителей).
3. Проверить правильность решения, применив метод узлового напряжения, предварительно упростить схему, заменив треугольник сопротивлений r₄, r₅ и r₆ эквивалентной звездой. Начертить расчётную схему с эквивалентной звездой и показать на ней токи.
4. Определить ток в резисторе r6 методом эквивалентного генератора.
5. Определить показание вольтметра и составить баланс мощностей для заданной схемы.
6. Построить в масштабе потенциальную диаграмму для внешнего контура.

Скачать решение варианта Задания 1 Расчёт линейных цепей постоянного тока

zadanie1-raschet-lineynyh-cepey-postoyannogo-toka.pdf (cкачиваний: 522)

Мощность в цепи с емкостью

Произведение тока и напряжения для емкости дает синусоиду, которая состоит из положительных и отрицательных полуволн, значит, средняя за период мощность равна 0.

Физический смысл состоит в том, что емкость за пол периода получает энергию, а затем пол периода возвращает ее в источник. Энергия накапливается в электрическом поле емкости, а затем возвращается в источник.  Частота синусоиды мощности вдвое больше частоты тока и напряжения.

Таким образом, на емкости не получается выделение тепла и никакой полезной мощности получить нельзя. Поэтому мощность, которая получается на емкости, называется реактивной и обозначается буквой – Qc.

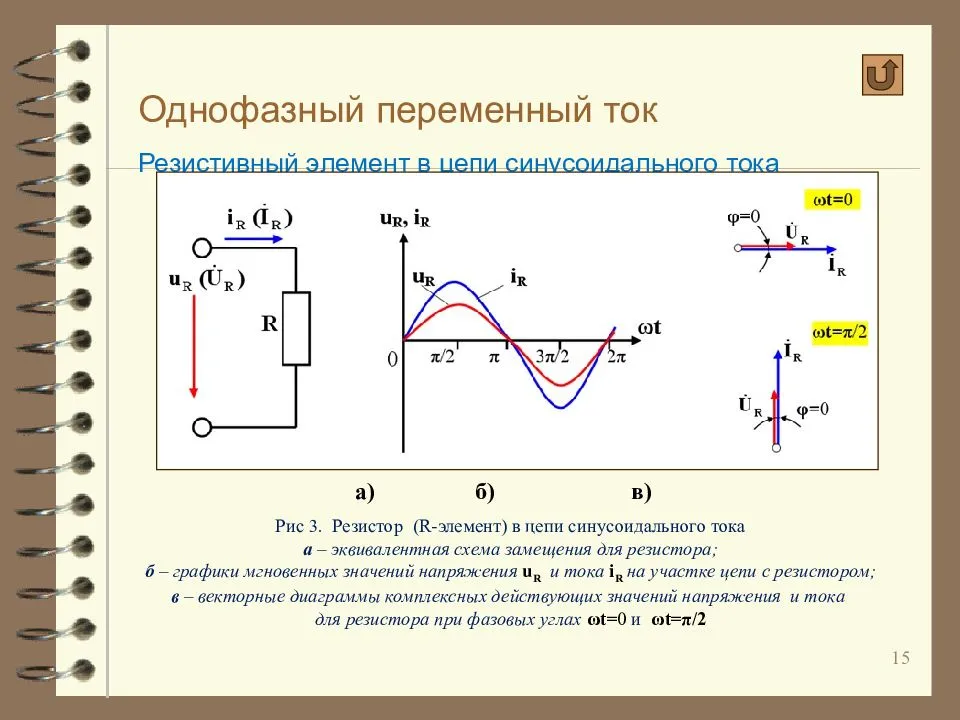
Кривые напряжения и тока в активном сопротивлении

Величину переменного напряжения или тока можно оценить значением амплитуды или средним значением за полупериод или действующим значением. При изменении напряжения или тока по закону синуса среднее значение напряжения определяется:

При большой частоте вращения ротора генератора, т. е. при большой частоте колебаний э. д. с. и силы тока, измерять их амплитуды на практике крайне неудобно. По этой причине ввели величины, названные действующими значениями э. д. с, силы тока и напряжения.

Действующим значением силы переменного тока называют силу такого постоянного тока, при прохождении которого по той же цепи и за то же время выделяется такое же количество теплоты, как и при прохождении переменного тока.

откуда

При синусоидальном законе действующие значения тока и напряжения:

Приборы электромагнитной системы, применяемые для измерений напряжений и токов на переменном токе, регистрируют действующие значения. Соответственно градуируются и шкалы этих приборов.

Ток, протекающий через индуктивность L (рис. 7), меняется по закону синуса /’ = Im sin(co/ + у;).

Задание 8

В цепи (рис. 8.1) в момент времени t = 0 происходит замыкание выключателя SB.
Определить токи ветвей цепи для t 0 и построить временные диаграммы соответствующих
токов и напряжений.

Решение

Будем считать, что источник ЭДС является идеальным. Используя
законы Кирхгофа, составим систему уравнений, описывающую

переходный процесс в цепи (с учетом направлений токов,
изображенных на рис. 8.1):

Общее решение однородного уравнения называется свободным током и в нашем случае будет равно:

где A и B – постоянные интегрирования.

Частным решением уравнения (8.7) является постоянный ток после окончания
переходного процесса (который теоретически продолжается бесконечно).
Этот ток называется установившимся током:

Таким образом, с учетом (8.8) и (8.9) общее решение неоднородного уравнения (8.7) имеет вид:

Теперь определим постоянная интегрирования A в общем решении (8.10).
Для этого используем закон коммутации для индуктивного элемента в
момент времени замыкания ключа t = 0. Так как ток в индуктивном элементе не
может измениться скачком, а до коммутации, т.е. в момент времени t = 0 он был равен нулю, то:

Теперь аналогичным образом определим напряжение uC. Из второго уравнения системы.
Найдем производную правой части уравнения (8.10) и тогда сможем определить uC:

Так как в момент коммутации uC = 0 и постоянная интегрирования A нам уже известна,
то мы можем найти постоянную интегрирования B:

Теперь мы можем получить закон нарастания тока iL и напряжения uC:

Подставим в первое уравнение системы (8.1) правые части (8.14) и (8.16),
и определим закон изменения тока через конденсатор.

Теперь остается только построить временные диаграммы токов и напряжений в
соответствующих ветвях.

Временная диаграмма изменения тока через катушку индуктивности и напряжения
на выводах катушки индуктивности

Временная диаграмма изменения тока через конденсатор и напряжения на выводах конденсатора

Временная диаграмма изменения тока через резистор и напряжения на выводах резистора

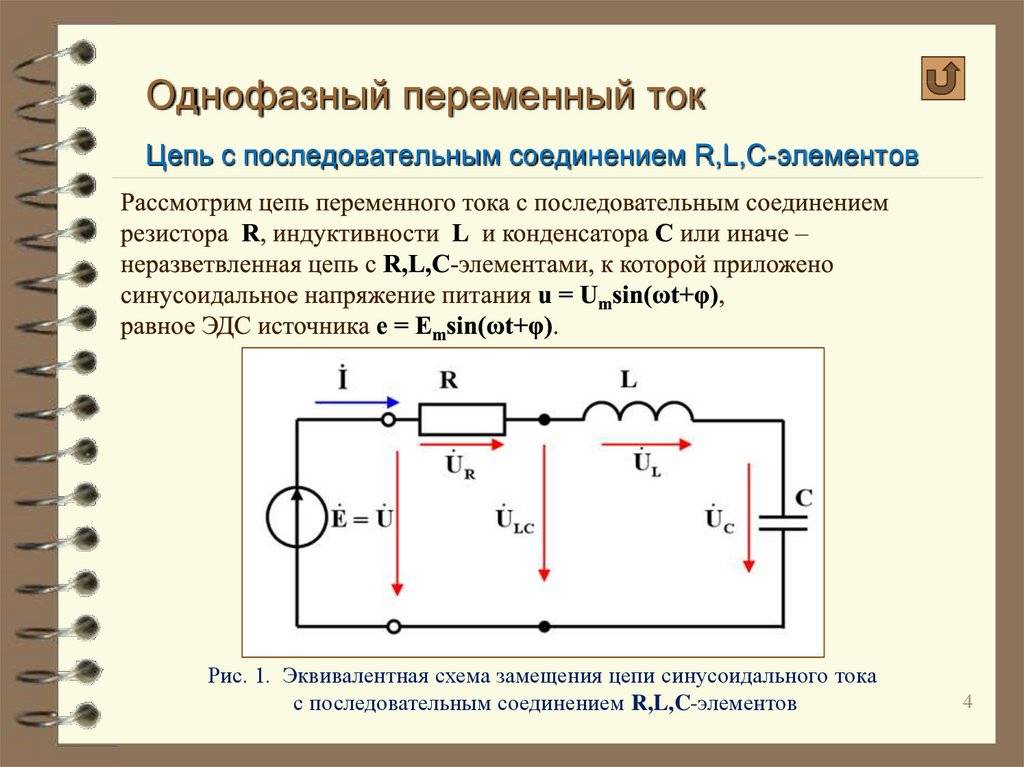
Цепи RLC

Цепи, которые содержат R, L и C, могут иметь разные варианты соединений. Цепи могут быть последовательными, разветвленными, и имеющие последовательные соединения в ветвях. Рассмотрим простые варианты. RLC последовательно.

В некоторых случаях цепи RL (моторы, трансформаторы и т. п.) имеют слишком маленький Cos φ. То есть в них слишком сильно влияние индуктивной составляющей. В такие цепи специально включают компенсационные конденсаторы, которые уменьшают фазовый сдвиг, Это разгружает источники электроэнергии от избыточной реактивной нагрузки, и обеспечивает значительную экономию электроэнергии.

Решение варианта ИДЗ №1 Линейные электрические цепи постоянного тока МИФИ

ФГБОУ ВПО НИЯУ МИФИ Озерский технологический институт – филиал НИЯУ МИФИ

Домашнее задание по электротехнике №1

Линейные электрические цепи постоянного тока

Для электрической схемы, в соответствии с вариантом, по заданным сопротивлениям и ЭДС выполнить следующее:

1. Составить систему уравнений, необходимых для определения токов по первому и второму законам Кирхгофа.

2. Найти все токи, пользуясь методом контурных токов.

3. Проверить правильность решения, применив метод узловых потенциалов, предварительно упростив схему, заменив треугольник сопротивлений R₄, R₅, R₆ эквивалентной звездой. Начертить расчетную схему с эквивалентной звездой и показать на ней токи.

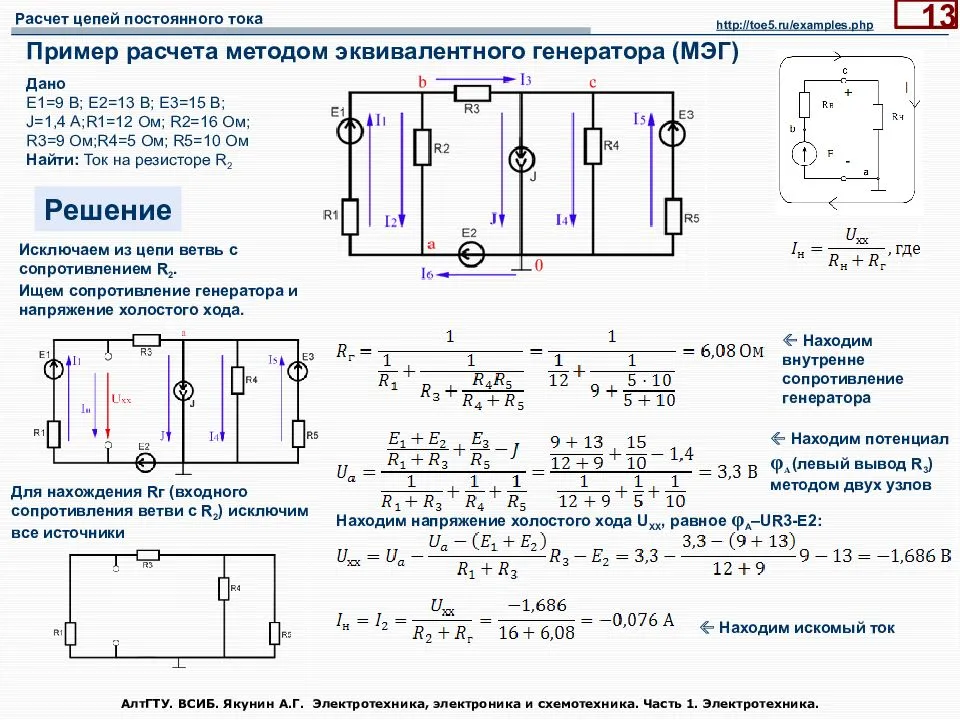
4. Определить ток в резисторе R₆ методом эквивалентного генератора.

5. Определить показание вольтметра и составить баланс мощностей для заданной схемы

Скачать Решение варианта ИДЗ №1 Линейные электрические цепи постоянного тока МИФИ

reshenie-idz-1-lineynye-elektricheskie-cepi-postoyannogo-toka-mifi.pdf (cкачиваний: 260)

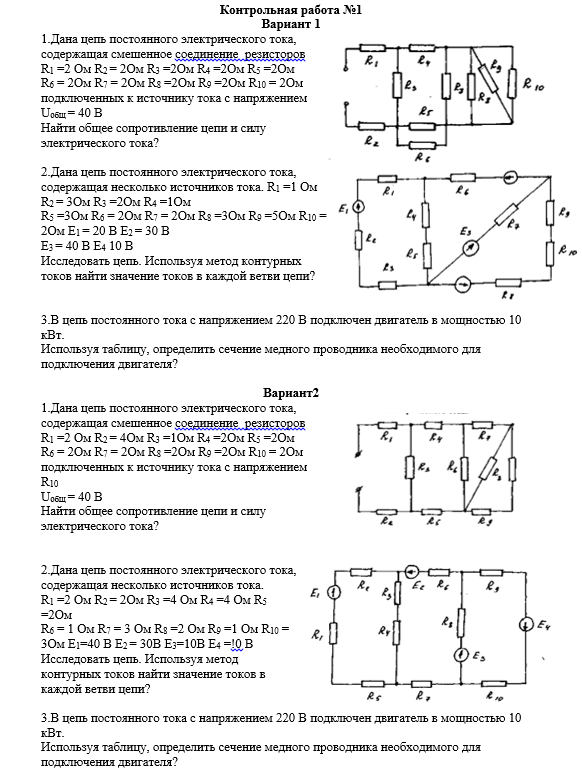
1 вариант

1. Конденсатор емкостью 250 мкФ включается в сеть пе­ременного тока. Определите емкостное сопротивление конденсатора при частоте 50 Гц.

2. Чему равен период собственных колебаний в колеба­тельном контуре, если индуктивность катушки равна 2,5 мГн, а емкость конденсатора 1,5 мкФ?

3. Напряжение меняется с течением времени по закону u = 40sin(10πt + π/6) В. Определите амплитуду, действующее значение, круговую частоту колебаний и началь­ную фазу колебаний напряжения.

4. Сколько оборотов в минуту должна совершать рамка из 20 витков проволоки размером 0,2 х 0,4 м в магнитном поле с индукцией 1 Тл, чтобы амплитуда ЭДС равнялась 500 В?

5. Напряжение в цепи изменяется по закону u = U_msin2π/_Tt, причем амплитуда напряжения 200 В, а период 60 мс. Какое значение принимает напряжение через 10 мс?

6. Катушка индуктивностью 75 мГн последовательно с конденсатором включена в сеть переменного тока с на­пряжением 50 В и частотой 50 Гц. Чему равна емкость конденсатора при резонансе в полученной сети?

7. В колебательном контуре конденсатору сообщили за­ряд 1 мКл, после чего в контуре возникли затухающие электромагнитные колебания. Какое количество теплоты выделится к моменту, когда максимальное напряжение на конденсаторе станет меньше начального максималь­ного значения в 4 раза? Емкость конденсатора равна 10 мкФ.

Метод контурных токов в цепи с источниками токов

Алгоритм метода контурных токов в цепи с источниками токов

1. Задаются направлением токов ветвей и обозначают их на схеме.
2. Строят контурные токи, проходящие через источники тока. Величина каждого такого контурного тока известна и равна току источника тока, через который проходит данный контурный ток (строим контурные токи так, что через источник тока проходит только один контурный ток!).
3. Определяют независимые контуры и их нумеруют. Независимые контуры, для которых составляются уравнения метода контурных токов, можно определить, если мысленно удалить источники тока (в нашем случае остается один независимый контур!).
4. Выбирают направление контурных токов (целесообразно в одну сторону) и составляют уравнения по методу контурных токов, обходя каждый контур в направлении его контурного тока.
5. Полученную систему алгебраических уравнений решают относительно неизвестных контурных токов.
6. Искомые токи по методу контурных токов находят как алгебраическую сумму контурных токов, проходящих по данной ветви. Токи в ветвях связи равны контурным токам.

4 вариант

1. Какой индуктивности катушку надо включить в коле­бательный контур, чтобы при емкости конденсатора 2 мкФ получить частоту 1 кГц?

2. Сила тока в электрической цепи изменяется по закону i = 3cos(100πt + π/3) А. Определите амплитуду силы то­ка, действующее значение силы тока, круговую частоту колебаний и начальную фазу колебаний.

3. Рассчитайте сопротивление конденсатора емкостью 250 мкФ, включенного в цепь переменного тока с часто­той 200 Гц.

4. Индуктивность колебательного контура равна 0,01 Гн, а емкость 1 мкФ. Конденсатор зарядили до разности по­тенциалов 200 В. Какой наибольший ток возникает в контуре в процессе электромагнитных колебаний?

5. Конденсатор и катушка соединены последовательно. Емкостное сопротивление конденсатора 5 кОм. Какой должна быть индуктивность катушки, чтобы резонанс наступил в цепи при частоте колебаний силы тока 20 кГц?

6. В колебательном контуре с индуктивностью 0,4 Гн и емкостью 20 мкФ амплитудное значение силы тока равно 0,1 А. Каким будет напряжение в момент, когда энергия электрического и энергия магнитного полей будут рав­ны? Колебания считать незатухающими.

7. В цепь переменного тока с частотой 400 Гц включена катушка индуктивностью 0,1 Гн. Определите, какой ем­кости конденсатор надо включить в эту цепь, чтобы осу­ществился резонанс.

Ответы на контрольную работа по физике Переменный ток 11 класс1 вариант
1. 12,7 Ом
2. 0,38 мс
3. 40 В; 28,4 В; 10π рад/с; π/6 рад
4. ≈ 3000 об/мин
5. 100 В
6. 135 мкФ
7. 0,047 Дж2 вариант
1. 13,2 Ом
2. 4233 Гц
3. 12 В; 8,5 В; 100π рад/с; 0
4. 24 А
5. 35,5 В
6. 120 мкДж; 40 мкДж
7. 5,04 В3 вариант
1. 4 мкФ
2. 3 А; 2,14 А; 157 рад/с; 0
3. 0,2 мс
4. 7,5 В
5. 25 нс
6. 0,6 Дж
7. u = 310 х sin 100pt; 0; 04 вариант
1. 12,7 мГн
2. 3 А; 2,13 А; 100π рад/ с; π/3 рад
3. 3,2 Ом
4. 2 А
5. 0,04 Гн
6. 10 В
7. 1,6 мкФ

2 вариант

1. Катушка с индуктивностью 35 мГн включается в сеть переменного тока. Определите индуктивное сопротивле­ние катушки при частоте 60 Гц.

2. Определите частоту собственных колебаний в колеба­тельном контуре, состоящем из конденсатора емкостью 2,2 мкФ и катушки с индуктивностью 0,65 мГн.

3. ЭДС индукции, возникающая в рамке при вращении в однородном магнитном поле, изменяется по закону е = 12sin100πt В. Определите амплитуду ЭДС, действую­щее значение ЭДС, круговую частоту колебаний и на­чальную фазу колебаний.

4. Конденсатор емкостью 800 мкФ включен в сеть пере­менного тока с частотой 50 Гц с помощью проводов, со­противление которых 3 Ом. Какова сила тока в конденса­торе, если напряжение в сети 120 В?

5. В цепь переменного тока с частотой 50 Гц включено ак­тивное сопротивление 5 Ом. Амперметр показывает силу тока 10 А. Определите мгновенное значение напряжения через 1/300 с, если колебания силы тока происходят по закону косинуса.

6. В колебательном контуре индуктивность катушки рав­на 0,2 Гн, а амплитуда колебаний силы тока 40 мА. Найдите энергию электрического поля конденсатора и магнитного поля катушки в момент, когда мгновенное значение силы тока в 2 раза меньше амплитудного значения.

7. Переменный ток возбуждается в рамке, имеющей 200 витков. Площадь одного витка 300 см2 Индукция маг­нитного поля 1,5 ⋅ 10-2 Тл. Определите ЭДС индукции че­рез 0,01 с после начала движения рамки из нейтрального положения. Амплитуда ЭДС равна 7,2 В.

Расчет

Для выяснения показателя активной мощности, необходимо знать полную мощность, для её вычисления используется следующая формула:

S = U \ I, где U – это напряжение сети, а I – это сила тока сети.

Этот же расчет выполняется при вычислении уровня передачи энергии катушки при симметричном подключении. Схема имеет следующий вид:

Схема симметричной нагрузки

Расчет активной мощности учитывает угол сдвига фаз или коэффициент (cos φ), тогда:

Очень важным фактором является то, что эта электрическая величина может быть как положительной, так и отрицательной. Это зависит от того, какие характеристики имеет cos φ. Если у синусоидального тока угол сдвига фаз находится в пределах от 0 до 90 градусов, то активная мощность положительная, если от 0 до -90 – то отрицательная. Правило действительно только для синхронного (синусоидального) тока (применяемого для работы асинхронного двигателя, станочного оборудования).

Также одной из характерных особенностей этой характеристики является то, что в трехфазной цепи (к примеру, трансформатора или генератора), на выходе активный показатель полностью вырабатывается.

Расчет трехфазной сети

Максимальная и активная обозначается P, реактивная мощность – Q.

Из-за того, что реактивная обуславливается движением и энергией магнитного поля, её формула (с учетом угла сдвига фаз) имеет следующий вид:

Для несинусоидального тока очень сложно подобрать стандартные параметры сети. Для определения нужных характеристик с целью вычисления активной и реактивной мощности используются различные измерительные устройства. Это вольтметр, амперметр и прочие. Исходя от уровня нагрузки, подбирается нужная формула.

Из-за того, что реактивная и активная характеристики связаны с полной мощностью, их соотношение (баланс) имеет следующий вид:

S = √P 2 + Q 2 , и все это равняется U*I .

Но если ток проходит непосредственно по реактивному сопротивлению. То потерь в сети не возникает. Это обуславливает индуктивная индуктивная составляющая – С и сопротивление – L. Эти показатели рассчитываются по формулам:

Сопротивление индуктивности: xL = ωL = 2πfL,

Сопротивление емкости: хc = 1/(ωC) = 1/(2πfC).

Для определения соотношения активной и реактивной мощности используется специальный коэффициент. Это очень важный параметр, по которому можно определить, какая часть энергии используется не по назначению или «теряется» при работе устройства.

При наличии в сети активной реактивной составляющей обязательно должен рассчитываться коэффициент мощности. Эта величина не имеет единиц измерения, она характеризует конкретного потребителя тока, если электрическая система содержит реактивные элементы. С помощью этого показателя становится понятным, в каком направлении и как сдвигается энергия относительно напряжения сети. Для этого понадобится диаграмма треугольников напряжений:

Диаграмма треугольников напряжений

К примеру, при наличии конденсатора формула коэффициента имеет следующий вид:

Для получения максимально точных результатов рекомендуется не округлять полученные данные.

3 вариант

1. Определите емкость конденсатора, сопротивление ко­торого в цепи переменного тока частотой 50 Гц равно 800 Ом.

2. В рамке, равномерно вращающейся в однородном маг­нитном поле, индуцируется ток, мгновенное значение ко­торого выражается формулой i = 3sin157t А. Определите амплитуду, действующее значение, круговую частоту ко­лебаний и начальную фазу колебаний силы тока.

3. Рассчитайте период собственных колебаний в колебательном контуре при емкости конденсатора 2 мкФ и ин­дуктивности катушки 0,5 мГн.

4. Рамка площадью 150 см2, содержащая 50 витков про­волоки, равномерно вращается со скоростью 120 об/мин в однородном магнитном поле с магнитной индукцией 0,8 Тл. Найдите амплитуду ЭДС индукции в рамке.

5. Амплитуда напряжения в колебательном контуре 100 В, частота колебаний 5 МГц. Через какое время на­пряжение будет 71 В?

6. Конденсатор емкостью 10 мкФ зарядили до напряже­ния 400 В и подключили к катушке. После этого возник­ли затухающие электрические колебания. Какое количе­ство теплоты выделится в контуре за время, в течение ко­торого амплитуда колебаний уменьшится вдвое?

7. Электроплитка сопротивлением 50 Ом включена в сеть переменного тока с частотой 50 Гц и напряжением 220 В. Запишите уравнения, выражающие зависимость напряжения и силы тока от времени для электроплитки. Чему равно мгновенное значение силы тока и напряже­ния через 1/100 с, если колебания происходят по закону синуса?

Метод векторных диаграмм

Мы уже пользуемся векторными диаграммами, по которым наблюдаем соотношения токов и напряжения в цепях переменного тока. Векторная диаграмма это стоячее изображение вращающихся векторов.

В предыдущих рассуждениях, было сказано, что линейно развернутая диаграмма переменного процесса, (в простом случае синусоидального), точно показывает  изменение мгновенного значения переменной величины, то есть происходит все именно так как показывает синусоида и каждая ее точка и есть переменная величина в данный момент. Но оказывается нам интересно не это, нам нужно знать какое значение тока и напряжения и мощности действует в цепи в течение времени, то есть действует длительное время, пока цепь работает.

Анализ синусоид нескольких величин, одновременно действующих в разных фазах, позволяет рассчитать все свойства и режимы работы цепи переменного тока, но гораздо проще это сделать, если отвлечься от синусоид и просто построить соотношение векторов, которые, собственно, и образуют эти синусоиды. Вся информация синусоид заложена в их радиус – векторах. Мы останавливаем эти векторы на рисунке, понимая, что они вращающиеся, но факт их вращения учитываем угловой частотой в расчетных формулах векторной диаграммы.

Итак, векторная диаграмма заменяет линейно развернутую синусоидальную диаграмму, потому, что любая информация, заложенная в синусоиду, есть и в соответствующем ей радиус-векторе.

Если нам приходится рассматривать несколько действующих одновременно синусоидальных процессов, то они изображаются векторной диаграммой, где длина каждого вектора, соответствует действующему значению синусоидальной величины, направление вектора соответствует начальной фазе, синусоидальной величины.

Результирующие значения одновременно действующих напряжений рассчитывается как векторная сумма, где угол между векторами определяется сдвигом фаз между ними.

Расчет цепей переменного тока сводится к расчету треугольников, которые состоят из соответствующих векторов.

Например, можно определить суммарное напряжение, частичные напряжения, и сдвиг фаз между ними.

На основании векторных диаграмм можно построить подобные векторным диаграммам треугольники сопротивлений и треугольники мощностей, решением которых можно определить соотношения сопротивлений, и мощности которые действуют в цепях переменного тока.

Векторная диаграмма напряжений представляет собой векторный треугольник напряжений

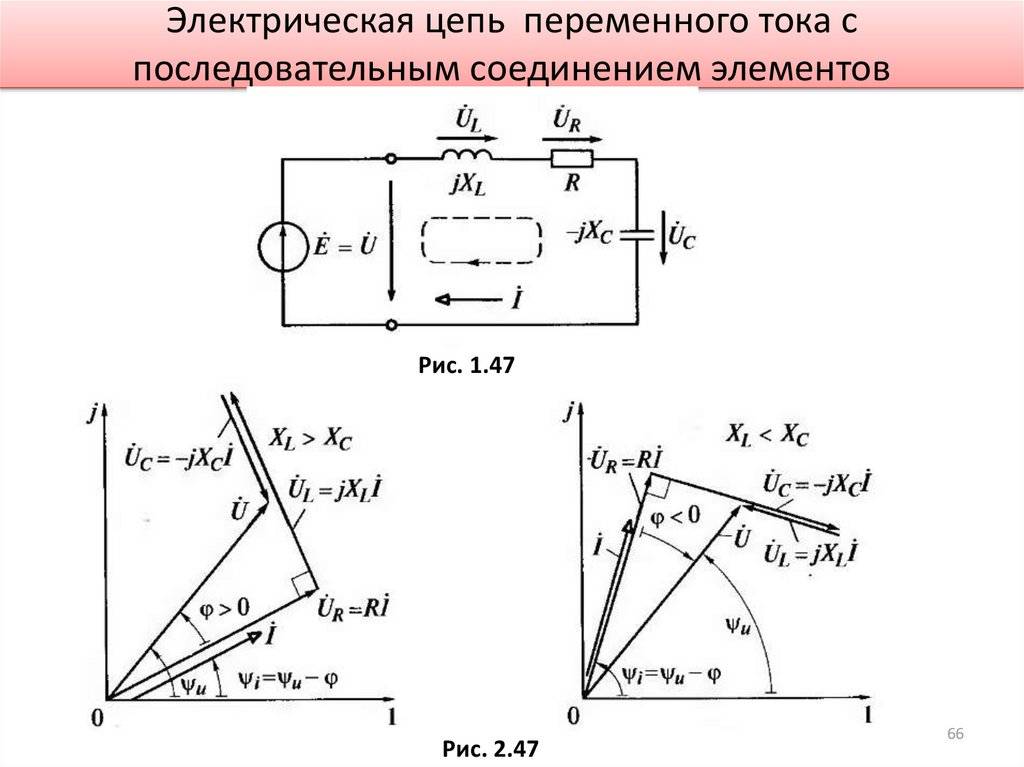
Последовательное соединение L R.

Любая катушка наматывается проволокой, а проволока обладает сопротивлением, которое приходится учитывать.

Получается, что реальная цепь, содержащая только L, просто невозможна. В некоторых случаях значением R пренебрегают, и получается, что вроде бы цепь с только L, на самом деле она конечно L R.

Реально, кроме проволоки, в цепи всегда есть и какие – то другие элементы R, поэтому интерес представляют именно цепи L R,

Ток, при последовательном соединении, один и тот же через все сопротивления, а напряжения разные, но общее напряжение не равно просто сумме напряжений на каждом сопротивлении, оно равно векторной сумме, то есть вектор общего напряжения равен сумме векторов напряжений на каждом участке. Для расчетов напряжений надо построить векторную диаграмму.

Векторная диаграмма строится так.

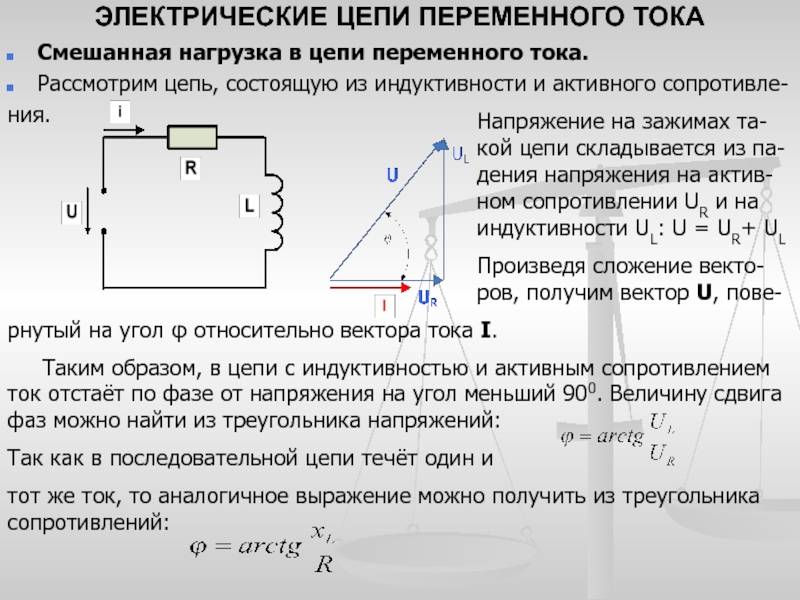
Емкость в цепи переменного тока

X_C =1/ ωc  

При включении емкости под переменное напряжение во время t=0, конденсатор полностью разряжен, напряжение на конденсаторе равно 0, и он начинает заряжаться. Поэтому мгновенно появляется ток зарядки. По мере зарядки конденсатора на нем начинает расти напряжение, которое тормозит процесс зарядки, а значит, ток зарядки начинает уменьшаться.

Когда U на конденсаторе достигает максимума, это значит, что оно достигло максимума напряжения источника, зарядка продолжаться не может, поэтому ток становится равным 0.

Синусоида тока (синяя) каждый раз пресекает ноль на π/2 раньше, чем (красная) синусоида напряжения.

То есть, максимальному напряжению на емкости соответствует ток, равный 0, а это значит, что ток на емкости С впереди напряжения на 90° или π/2