Комплексные числа для расчета электрических цепей синусоидального тока

Метки

• алгоритм расчет цепей при несинусоидальных периодических воздействиях
• алгоритм расчета цепей периодического несинусоидального тока
• баланс мощностей
• ВАХ нелинейного элемента
• Векторная диаграмма
• ветви связи
• взаимная индуктивность
• взаимная проводимость
• вольт-амперная характеристика нелинейного элемента
• второй закон Кирхгофа
• второй закон Кирхгофа для магнитных цепей
• входная проводимость
• гармоники напряжения
• гармоники тока
• Генератор напряжения
• генератор тока
• главные контуры
• графический метод расчета нелинейных электрических цепей
• динамическое сопротивление
• дифференциальное сопротивление
• емкость двухпроводной линии
• емкость коаксиального кабеля
• емкость конденсатора
• емкость однопроводной линии
• емкость плоского конденсатора
• емкость цилиндрического конденсатора
• закон Ампера
• закон Био Савара Лапласа
• закон Ома
• закон полного тока
• закон электромагнитной индукции
• Законы Кирхгофа
• индуктивность
• индуктивность двухпроводной линии
• индуктивность однопроводной линии
• индуктивность соленоида
• катушка со сталью
• Конденсатор в цепи постоянного тока
• контурные токи
• коэффициент амплитуды
• коэффициент гармоник
• коэффициент искажения
• коэффициент магнитной связи
• коэффициент мощности трансформатора
• коэффициент трансформации
• коэффициент формы
• кусочно-линейная аппроксимация
• магнитная постоянная
• магнитная цепь
• магнитный поток рассеяния
• метод активного двухполюсника
• метод двух узлов
• метод контурных токов
• метод наложения
• метод узловых напряжений
• метод узловых потенциалов
• метод эквивалентного генератора
• метод эквивалентного источника ЭДС
• Метод эквивалентных преобразований
• методы расчета магнитных цепей
• независимые контуры
• нелинейный элемент
• несинусоидальный периодический ток
• обобщенный закон Ома
• опорный узел
• основной магнитный поток
• параллельное соединение конденсаторов
• первый закон Кирхгофа
• первый закон Кирхгофа для магнитных цепей
• последовательное соединение конденсаторов
• последовательный колебательный контур
• постоянная составляющая тока
• потери в меди
• потери в стали
• приведенный трансформатор
• Примеры расчета схем при несинусоидальных периодических воздействиях
• принцип взаимности
• принцип компенсации
• расчет гармоник тока
• расчет магнитной цепи
• расчет нелинейных цепей постоянного тока
• расчет цепей несинусоидального тока
• Расчет цепи конденсаторов
• расчет цепи с несинусоидальными периодическими источниками
• Резонанс в электрической цепи
• решение задач магнитные цепи
• сила Ампера
• сила Лоренца
• Символический метод
• собственная проводимость
• статическое сопротивление
• сферический конденсатор
• теорема об эквивалентном источнике
• теорема Тевенена
• топографическая диаграмма
• Трансформаторы
• трехфазная система
• удельная энергия магнитного поля
• уравнения трансформатора
• Цепи с конденсаторами
• частичные токи
• чередование фаз
• ЭДС самоиндукции
• эквивалентная схема трансформатора
• электрическая постоянная
• электроемкость
• энергия магнитного поля

Комплекс действующего значения

Изображение синусоидальных токов и напряжений с помощью векторов на комплексной плоскости. Комплексная амплитуда.

Комплекс действующего значения

Мы уже изображали токи и напряжения в виде векторов, остается лишь взять комплексную плоскость:

В отличие от математики, мнимая единица обозначается буквой , т.к. обозначает мгновенное значение тока.

Длина комплексного вектора равна амплитудному или действующему значению. В первом случае её называют комплексной амплитудой

, во втором –комплексом действующего значения . Угол поворота соответствует фазе .

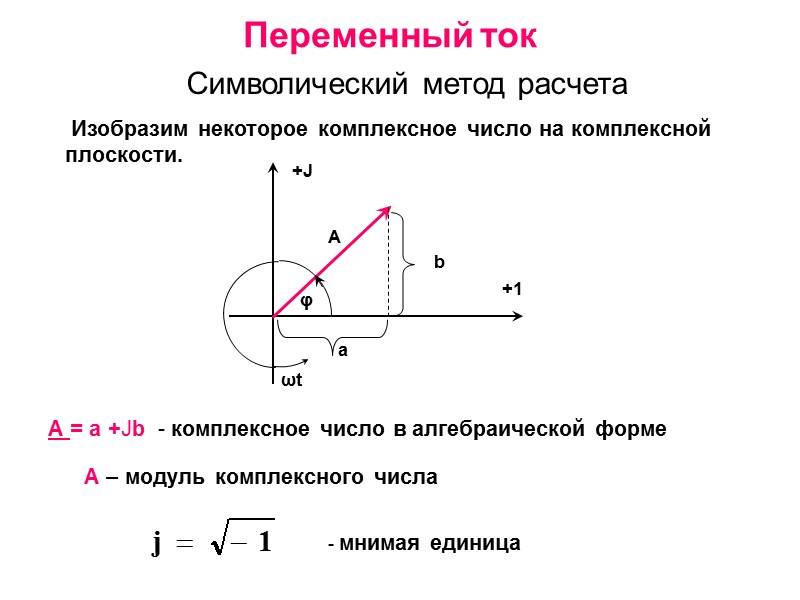
Как известно из математики, комплексные числа имеют две основные формы записи: алгебраическая и показательная (экспоненциальная)

Есть ещё тригонометрическая форма, но она является как бы переходом от показательной к алгебраической, поэтому ей не уделяют внимание

– это комплексная амплитуда в показательной форме записи.

Это не простое комплексное число, это временная функция, поэтому, для того, чтобы отличить её от простых комплексных чисел, которые обозначают подчёркиванием, комплексную амплитуду обозначают точкой вверху.

Чтобы получить комплекс действующего значения, нужно комплексную амплитуду поделить на :

Это тоже комплексная функция времени, поэтому обозначается точкой вверху.

Аналогично токам вводятся комплексные амплитуды и комплексы действующих значений напряжений.

Для того чтобы перейти от комплексов к мгновенным значениям, нужно взять проекции комплексной амплитуды на мнимую ось:

Вектор комплексной амплитуды, также как вектор комплекса действующего значения, вращается на комплексной плоскости с угловой частотой (циклической частотой) . Работать с такими векторами невозможно. Чтобы остановить этот вектор, берут время = 0: ; тогда

Переход от показательной формы к алгебраической осуществляется через тригонометрическую форму. Необходимо взять проекции комплексного вектора на действующую ось – , и на мнимую ось .

Для перехода от алгебраической формы к экспоненциальной используется следующая формула:

Внимание. Эта формула работает, если вектор находится в I или IV четверти комплексной плоскости, т.е

когда , если (вектор находится во II или III четверти), тогда нужно пользоваться другой формулой:

т.е. умножение комплексного вектора на эквивалентно его повороту на комплексной плоскости на раз, а умножение на –

эквивалентно повороту на раз.

Выводы:

Синусоидальным периодическим функциям токов и напряжений можно поставить в соответствие временные функции на комплексной плоскости, которые называются изображениями и несут всю информацию о реальных функциях (токов и напряжений), об их амплитудах и фазах, поэтому для комплексных функций выполняются законы Кирхгофа. Сложение, вычитание, деление, умножение, дифференцирование и интегрирование реальных функций можно заменить на те же операции с комплексными изображениями.

Дата добавления: 2016-05-28 ; ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

3.2 Второй закон Кирхгофа

Второй закон Кирхгофа применяется к контурам и
формулируется следующим образом: алгебраическая сумма падений напряжений по
любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих
вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений
равно нулю.

Для постоянных напряжений:

Для переменных напряжений:

Иными словами, при обходе цепи по контуру, потенциал,
изменяясь, возвращается к исходному значению. Если цепь содержит m ветвей, из
которых содержат источники тока ветви в количестве m_i, то она
описывается m-m_i– (у – 1) уравнениями напряжений.
Частным случаем второго правила для цепи, состоящей из одного контура, является
закон Ома для этой цепи.

Рисунок 2 – Схема электрическая принципиальная расчетной цепи

В итоге на схеме, рисунок 2, остаётся четыре узла, так как узел есть
точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения
двух линий на электрической схеме поставлена точка, то в этом месте есть
электрическое соединение двух линий, в противном случае его нет. Узел, в
котором сходятся две ветви, одна из которых является продолжением другой,
называют устранимым или вырожденным узлом.

Рассчитываю количество уравнений по первому и второму закону Кирхгофа.

у = 5 – число узлов;

в = 6 – число ветвей;

в_ит = 0 – число ветвей с источником тока.

Количество уравнений по первому закону Кирхгофа n1 = у −1 = 4 Количество уравнений по второму
закону Кирхгофа n2 = в − в_ит −(у − 1) = 4

Согласно первому заданию составляю системы уравнений по первому и второму
законам Кирхгофа. По 1-му закону Кирхгофа для (у-1) узлов схемы, с учетом токов
от источников тока, где y –
число узлов схемы. Уравнение для последнего узла не составляют, т.к. оно
совпало бы с уравнением, полученным при суммировании уже составленных уравнений
для предыдущих узлов (т.е. линейно-независимых уравнений – (y-1)). При составлении уравнений
следуют правилу: если ток выходит из узла, то его записывают со знаком
“-“, если входит – то со знаком “+”.

Уравнения по первому закону Кирхгофа:

1)       I_{1 +} I₂– I₃ = 0 (по 1 точке)

)         -I₁ – I₄ + I₅ = 0
(по 2 точке)

)         I₃ – I₄ – I₆ = 0 (по 3 точке)

) -I₂ – I₅ – I₆ = 0 (по 4 точке)

Для составления уравнений по второму закону Кирхгофа, используется
нарисованная схема, показанная на рисунке 3.

Рисунок 3 – Схема электрическая принципиальная расчетной цепи

Уравнения по второму закону Кирхгофа:

I.        I₁R₁ + I₂R₂
+ I₃R₃ = E₃ + E₂+ E₁

II.      -I₁R₁ – I₄R₄
+ I₅R₅ = E₁.  I₃R₃ + I₄R₄
+ I₆R₆ = E₃

IV.     -I₂R₂ – I₅R₅
– I₆R₆ = E₂

4. Метод контурных токов

Метод основан на введении промежуточной неизвестной величины – контурного
тока и использовании 2 закона Кирхгофа.

Контурный ток – собственный ток каждого независимого контура.

Реальный ток в ветвях определяется как алгебраическая сумма
соответствующих контурных токов. Число неизвестных в этом методе равно числу
уравнений, которые необходимо было бы составить для схемы по второму закону
Кирхгофа, то есть числу независимых контуров [(m – m_i) – (у – 1)].

Для каждого независимого контура (ячейки) составляют расчетное контурное
уравнение согласно правилу: левая часть равна сумме произведений контурного
тока на собственное сопротивление этого контура, взятое со знаком плюс, и
контурных токов прилегающих контуров на сопротивления смежных ветвей, взятых со
знаком минус: правая часть равна алгебраической сумме ЭДС этого контура –
контурной ЭДС.

Пусть электрическая цепь содержит n контуров (независимых). Согласно II
закону Кирхгофа получаем следующую систему из n линейных уравнений:

При этом следует считать , если условные положительные направления контурных токов в
одной ветви контуров K и m совпадают, и , если они противоположны.

где D1 D2 Dn – дополнение

D – определитель системы.

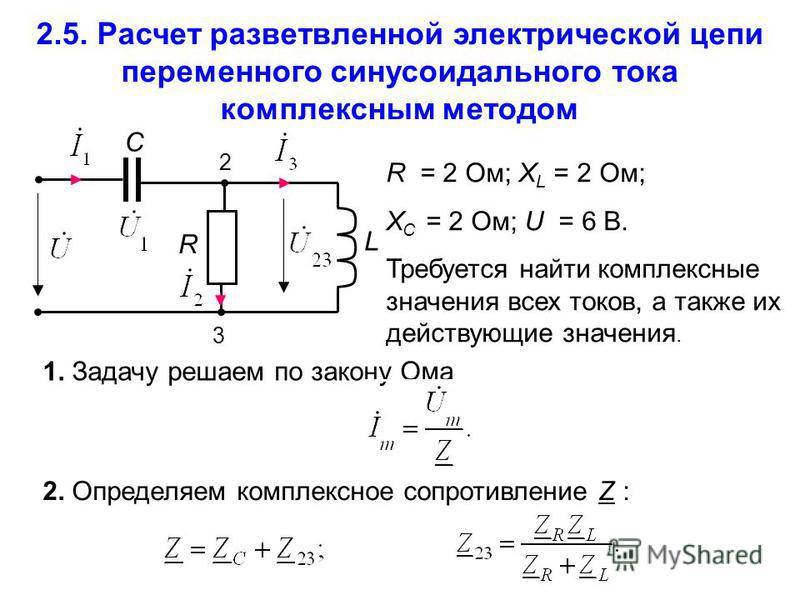
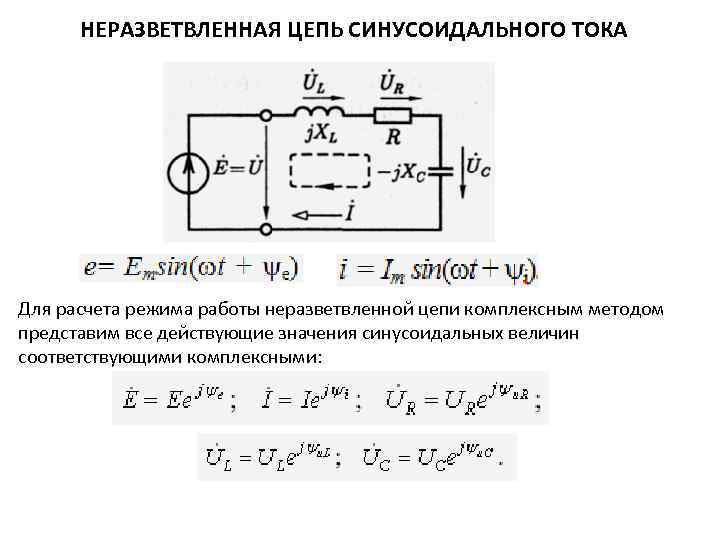
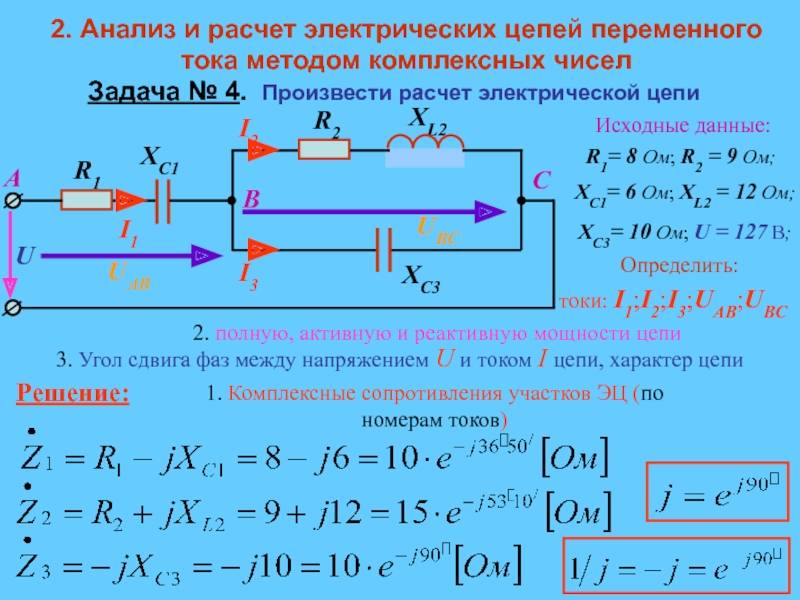
Расчёт установившегося режима в цепи переменного тока комплексным методом
выполняется в следующей последовательности:

Составляется электрическая схема, на которой все источники и пассивные
элементы представляются комплексными величинами соответственно напряжений,
токов, сопротивлений (проводимостей). Выбирается условно положительное
направление для комплексных значений напряжений, ЭДС и токов. Согласно
уравнениям электрических цепей (Ома, Кирхгофа) в комплексной форме составляются
алгебраические уравнения для рассчитываемой цепи. Уравнения цепи разрешаются
относительно искомых переменных (токов, напряжений) в их комплексной форме.

Заказать решение ТОЭ

• Метрология Электрические измерения
• Пигарев А.Ю. РГЗ по электротехнике и электронике в Multisim
• Теория линейных электрических цепей ТЛЭЦ
  • —
    Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи: задание на контрольные работы № 1 и 2 с методическими указаниями для студентов IV курса специальности Автоматика, телемеханика и связь на железнодорожном транспорте
    • —
      Контрольная работа №1
    • —
      Контрольная работа №2
• Электротехника и основы электроники
  • —
    Электротехника и основы электроники: Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений / Соколов Б.П., Соколов В.Б. – М.: Высш. шк., 1985. – 128 с, ил
    • —
      Контрольная работа № 1 Электрические цепи
    • —
      Контрольная работа № 2 Трансформаторы и электрические машины
    • —
      Контрольная работа № 3 Основы электроники
• Теоретические основы электротехники ТОЭ
  • —
    Артеменко Ю.П., Сапожникова Н.М. Теоретические основы электротехники: Пособие по выполнению курсовой работы МГТУ ГА 2009
  • —
    Переходные процессы Переходные процессы в электрических цепях
  • —
    Теоретические основы электротехники Методические указания и контрольные задания для студентов технических специальностей вузов
    • —
      Задание 1 Линейные электрические цепи постоянного и синусоидального тока
      • —
        Задача 1.1 Линейные электрические цепи постоянного тока
      • —
        Задача 1.2 Линейные электрические цепи синусоидального тока
    • —
      Задание 2 Четырехполюсники, трехфазные цепи, периодические несинусоидальные токи, электрические фильтры, цепи с управляемыми источниками
  • —
    Теоретические основы электротехники сб. заданий Р.Я. Сулейманов Т.А. Никитина Екатеринбург УрГУПС 2010
  • —
    Трехфазные цепи. Расчет трехфазных цепей
  • —
    УГТУ-УПИ Решение ТОЭ Билеты по ТОЭ
  • —
    Электромагнитное поле Электростатическое поле Электростатическое поле постоянного тока в проводящей среде Магнитное поле постоянного тока

Как найти комплексное значение тока

Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

Комплексное напряжение

2020-04-07 1873Символический метод расчета

Электрических цепей переменного

Синусоидального тока

КОМПЛЕКСНЫЕ ТОКИ И НАПРЯЖЕНИЯ

Математическое введение (формула Эйлера)

Между синусоидальными и экспоненциальными (показательными) функциями существует простая зависимость, которая получила название формулы Эйлера,

,

где

— мнимая единица. В частности, если , .

Формула Эйлера применяется для перевода комплексных чисел из показательной формы в алгебраическую. В показательной форме комплексное число

содержит модульz и аргумент : . В алгебраической форме комплексное число имеет действительную часть x и мнимую часть y:

. , . (4.1)

Решив эти уравнения относительно

и , получаем формулы для перевода комплексных чисел из алгебраической формы в показательную , . (4.2)

В задачах электротехники пределы изменения

обычно выбирают в пределах от до и вычисляют по формуле

Для запоминания формул (4.1) и (4.2), предназначенных для перевода комплексных чисел из одной формы записи в другую, можно использовать треугольник, похожий на треугольник сопротивлений (рис. 4.1).

Рис. 4.1. Треугольник, иллюстрирующий зависимости между действительной и мнимой частями комплексного числа, с одной стороны, и его модулем и аргументом, с другой стороны

Комплексный ток

В электрической цепи с источником синусоидального напряжения протекают синусоидальные токи. Пусть один из них равен

,

где I — действующее значение тока. Запишем соответствующую косинусоидальную функцию

Затем с помощью формулы Эйлера составим комплексную функцию

Множитель

одинаков для всех токов цепи. Комплексное число характеризует ток рассматриваемой ветви.

И 4.1

Определение . Комплексное число называют комплексным током. Модуль комплексного тока равен действующему значению синусоидального тока, аргумент комплексного тока – начальной фазе синусоидального тока.

Комплексное напряжение

Синусоидальному напряжению можно сопоставить комплексное напряжение аналогично тому, как синусоидальному току был поставлен в соответствие комплексный ток:

Здесь U – действующее значение напряжения;

— его начальная фаза.

И 4.2

Определение . Комплексное число называют комплексным напряжением. Модуль комплексного напряжения равен действующему значению синусоидального напряжения, аргумент комплексного напряжения – начальной фазе синусоидального напряжения.

Преобразование синусоидальных токов и напряжений в комплексные числа (комплексные токи и напряжения) позволяет преобразовать тригонометрические уравнения, составленные по законам Кирхгофа для синусоидальных токов и напряжений, в алгебраические уравнения для комплексных токов и напряжений. Благодаря тому, что в уравнениях для комплексных токов можно опустить множитель

, общий для всех токов, решение алгебраических уравнений оказывается не столь громоздким, как решение тригонометрических уравнений. Решив систему уравнений Кирхгофа относительно комплексных токов, можно затем по комплексным токам определить синусоидальные токи.

Источник