Как определить?
Для решения задачи нахождения мощности можно воспользоваться различными способами. Все они доступны для применения даже при знаниях в области физики и электротехники на уровне школьной программы.
Чаще мощность находят через определение тока, иногда можно обойтись без промежуточных процедур и определит ее сразу.
Смотрим в техпаспорт
Обычно потребляемая мощность указывается в паспорте или описании устройства и дублируется на фирменной табличке-шильдике. Последняя находится на задней стенке корпуса или его основании.
В случае отсутствия описания этот параметр можно узнать по интернету, для чего достаточно воспользоваться поиском по названию устройства.
Указываемая производителем техники мощность относится к пиковой и потребляется от сети только при полной нагрузки, что встречается достаточно редко. Образовавшаяся разница рассматривается как запас. На нормативном уровне этот запас определяют через коэффициент мощности.
Закон Ома в помощь
Мощность большинства бытовых электрических устройств можно довольно точно оценить экспериментально-расчетным путем с привлечением известного еще со средней школы закона Ома. Этот эмпирический закон связывает между собой напряжение, ток и сопротивление R нагрузки как:
P = U2/R. U = 230 В, а сопротивление измеряется тестером. Далее следует простой расчет по формуле P = 48 400/R Вт.
Например, при R = 200 Ом получаем мощность Р = 240 Вт.
Метод не учитывает так называемое реактивное сопротивление прибора, которое создается в первую очередь входными трансформаторами и дросселями, и поэтому получаемая оценка дает некоторое завышение.
Используем электросчетчик
При определении мощности по счетчику можно поступить двумя различными способами. В обоих случаях от бытовой сети должен питаться только тестируемый прибор. Все без исключения остальные потребители должны быть отключены.
При первом подходе для замера мощности привлекается оптический индикатор счетчика, интенсивность вспышек которого пропорциональна потребляемой мощности. Коэффициент пропорциональности указан на лицевой панели в единицах imp/kWh или имп/кВтч, рисунок 1, где imp – количество импульсов (вспышек индикатора) на один киловатт час.
Рисунок 1. Лицевая панель бытового счетчика электроэнергии с оптическим индикатором
После включения исследуемого устройства необходимо начать считать вспышки индикатора на протяжении 15 или 20 минут. Затем полученное значение умножается на 3 или на 4 (при 20- или 15-минутном интервале замера, соответственно) и делится на коэффициент с лицевой панели. Результат выкладки дает мощность прибора в кВт, который в ряде случаев умножением на 1000 удобно перевести в Ватты.
При втором подходе также используется 15- или 20-минутный интервал времени, но расход электроэнергии определяется уже по цифровой шкале. Например, при разности показаний за 20 минут 0,2 кВт×час мощность агрегата составляет 0,2 × 3 = 0,6 кВт или 600 Вт.
Ваттметром
Современный бытовой измеритель мощности или ваттметр удобен для использования, так как:
- включается непосредственно в разрыв цепи, для чего снабжен вилкой и розеткой, см. рисунок 2;
- оборудован легко читаемым цифровым индикатором и снабжен внутренними цепями автоматической настройки, что исключает ошибки в показаниях;
- отличается хорошими массогабаритными показателями.
Прибор готов к работе немедленно после включения.
Рис. 2. Цифровой бытовой ваттметр
Единственный его недостаток – узкая специализация, поэтому этот прибор редко встречается в домашнем хозяйстве.
Закон Ома — калькулятор
Данный онлайн калькулятор закона Ома позволяет определить взаимосвязь между силой тока, электрическим напряжением, сопротивлением проводника и мощностью. Для расчета введите любые два параметра и нажмите кнопку расчет:
Для закрепления понимания работы закона Ома, приведем несколько задач для самостоятельного решения.
| Какая должна быть минимальным мощность этого резистора? Ответ:В соответствии с круговой диаграммой Р = I2*R = 0,12*50 = 0,5 Вт. Таким образом, минимальная мощность должна быть не менее 0,5 Вт, но рекомендуется взять более мощный для дополнительной надежности и долговечности. | ||
| Какой будет ток в цепи? Ответ:Это простой пример закона Ома. Напряжение и сопротивление известны, так что мы можем вычислить ток по формуле:I = V / R = 6 / 1,2 = 5 А. | ||
| Электронагреватель (резистор) мощностью 1 кВт подключен в цепь с током 10A. Какое будет падение напряжения на нагревателе? Ответ:Напряжение может быть выражено через ток и мощность по формуле: V = P / I = 1000/10 = 100 В |
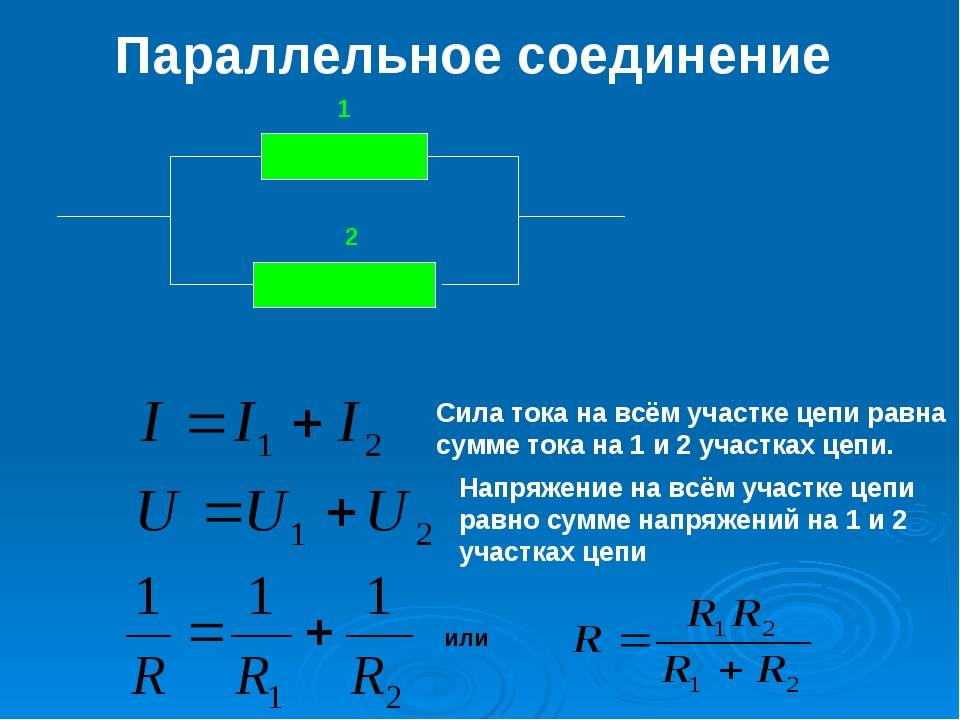
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
- Таким образом, протекающий общий ток в цепи можно определить как:
- I = I1 + I2
- Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
- Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
- Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
- Таким образом, общий ток будет равен:
- I = 0,545 мА + 0,255 мА = 0,8 мА
- Это также можно проверить, используя закон Ома:
- I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
- где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
- И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами.
Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
- R1 = 1 Ом;
- R2 = 2 Ом;
- R3 = 3 Ом;
- R4 = 6 Ом;
- R5 = 9 Ом;
- R6 = 18 Ом;
- R7 = 2Ом;
- R8 = 2Ом;
- R9 = 8 Ом;
- R10 = 4 Ом.
Напряжение, поданное на схему:
U = 24 В.
Требуется рассчитать токи на всех резистивных элементах.
Исходная цепь
Для расчётов применяется закон Ома:
I = U/R, подставляя вместо R эквивалентное сопротивление.
Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте. Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения
Делают расчёты для каждого такого звена, после – всей цепи целиком
Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком.
На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
- АВ – участок, имеющий две параллельных ветви;
- ВС – отрезок, вмещающий в себя последовательное сопряжение;
- CD – отрезок схемы с расположением трёх параллельных цепочек.
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте.
Последовательно соединённые резисторы R2 и R3
Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов.
Смешанное включение на участке CD
Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:
- Rэкв.2,3 = R2+R3=2 + 3 = 5 Ом;
- Rэкв.7,8 = (R7*R8)/R7 + R8 = (2*2)/2 + 2 = 1 Ом;
- Rэкв.7,8,9 = Rэкв.7,8 + R9 = 1 + 8 = 9 Ом.
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже.
Результат первого свёртывания
Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
- Rэкв.AB = (R1*Rэкв 2,3)/R1 + Rэкв 2,3 = (1*5)/1 + 5 = 0,83 Ом;
- Rэкв.BC = R4 + R5 = 6 + 9 = 15 Ом;
- 1/Rэкв.CD = 1/R6 + 1/Rэкв.7,8,9 + 1/R10 = 1/18 + 1/9 + 1/4 = 0,05 + 0,11 + 0,25 = 0,41 Ом.
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже.
Результат последующего свёртывания
Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков:
Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом.
Далее, используя закон Ома, находят ток в последнем последовательном участке:
I = U/ Rэкв. = 24/56,83 = 0,42 А.
Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:
- UAB = I* Rэкв.AB= 0,42*0,83 = 0,35 В;
- UBC = I* Rэкв.BC= 0,42*15 = 6,3В;
- UCD = I* Rэкв.CD = 0,42*0,41 = 0,17 В.
Следующим шагом станет определение токов на параллельных отрезках AB и CD
- I1 = UAB/R1 = 0,35/1 = 0,35 А;
- I2 = UAB/Rэкв.2,3 = 0,35/5 = 0,07 А;
- I3 = UCD/R6 = 0,17/18 = 0,009 А;
- I6 = UCD/Rэкв.7,8,9= 0,17/9 = 0,02 А;
- I7 = UCD/R10 = 0,17/4 = 0,04 А.
Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9.
U9 = R9*I6 = 8*0,02 = 0,16 В.
Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9.
U7,8 = UCD – U9= 0,17 – 0,16 = 1 В.
После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:
- I4 = U7,8/R7 = 1/2 = 0,5 A;
- I5 = U7,8/R8 = 1/2 = 0,5 A.
Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется параллельное соединение резисторов, а для делителей напряжения – последовательное. На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора. Мощность также входит в состав маркировки, нанесенной на корпус элемента. Единицами измерения сопротивления служат ом (1 Ом), килоом (1000 Ом) и мегаом (1000000 Ом). Ассортимент резисторов находится в пределах от долей ома до нескольких сотен мегаом. Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Для соединения резисторов в схемах используются три разных способа подключения – параллельное, последовательное и смешанное. Каждый способ обладает индивидуальными качествами, что позволяет применять данные элементы в самых разных целях.
Закон Ома и резистор
Резисторы являются пассивными элементами, которые оказывают сопротивление потоку электрического тока в цепи. Резистор, который функционирует в соответствии с законом Ома, называется омическим сопротивлением. Когда ток проходит через такой резистор, то падение напряжения на его выводах пропорционально величине сопротивления.
Формула Ома остается справедливой и для цепей с переменным напряжением и током. Для конденсаторов и катушек индуктивности закон Ома не подходит, так как их ВАХ (вольт-амперная характеристика) по сути, не является линейной.
Формула Ома действует так же для схем с несколькими резисторами, которые могут быть соединены последовательно, параллельно или иметь смешанное соединение. Группы резисторов, соединенные последовательно или параллельно могут быть упрощены в виде эквивалентного сопротивления.
В статьях о параллельном и последовательно соединении более подробно описано как это сделать.
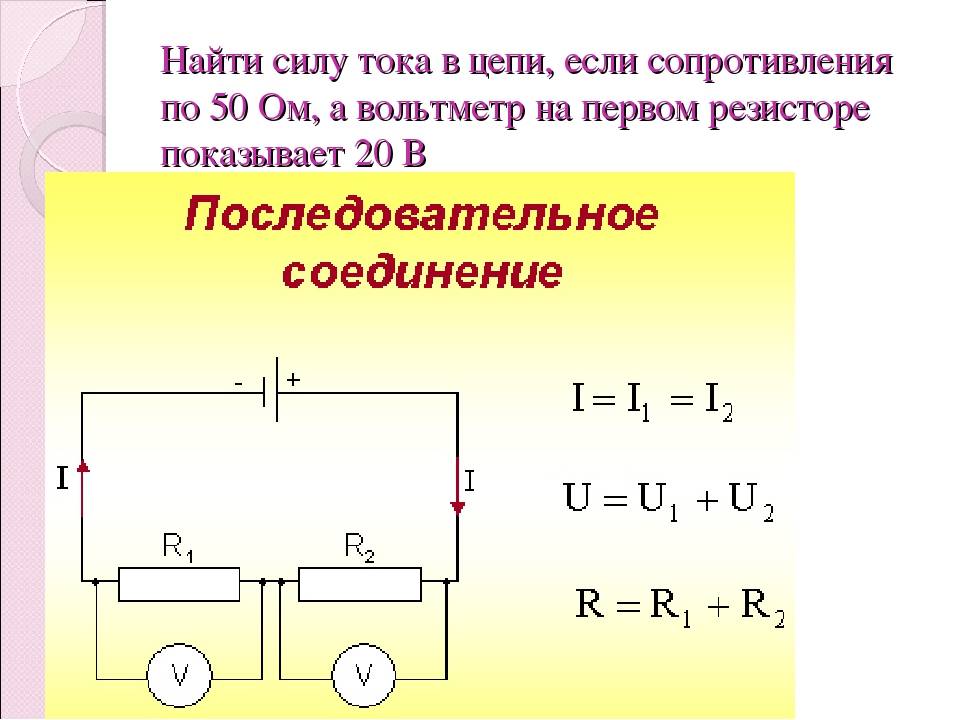
чему равен общий ток цепи и напряжение на участке при последовательном соединение???
Общее сопротивление при последовательном соединении равно сумме сопротивлений Rсумм=R1+R2+R3…
Ток через все сопротивления протекает один ( I ). Поэтому ток вычисляешь как Отношение напряжения источника U к Rсумм.
I=U/Rсумм
Мощность
P=U*I или P=I*I*R (так как U=I*R).
тогда,
P1=I*I*R1
P2=I*I*R2
P3=I*I*R3
1) сумма
2)напряжение на участке цепи умножить на ток. При том ток, при последовательном соединении одиноковй в любой точке цепи
При последовательном соединении узлов нет. Ток цепи определяется делением приложенного напряжения в вольтах (V) на
сопротивление цепи в омах (R). I=V : R. Падение напряжения на участке будет равнятся сопротивлению участка
помноженному на ток.
Общее сопротивление равно сумме всех сопротивлений.
Мощность участка равняется падению напряжения на участке помноженному на ток.
Это Закон Ома.
А вообще-то это все в школьном учебнике физики в разделе-Электричество.
Напряжение на участке цепи
Под
напряжением на некотором участке
электрической цепи понимают разность
потенциалов между крайними точками
этого участка.
На
рис. 1-13 изображен участок цепи, на котором
есть резистор сопротивлением
и нет ЭДС. Крайние точки этого участка
обозначены буквами a
и b.
Пусть ток течет от точки a
к точке b.
Рис.
1-13. Участок электрической цепи
На
участке без ЭДС ток течет от более
высокого потенциала к более низкому.
Следовательно, потенциал
точки
a
выше потенциала
точки b
на величину, равную произведению тока
на сопротивление :
.
В
соответствии с определением, напряжение
между точками a
и b
.
(1-8)
Другими
словами, напряжение на резисторе равно
произведению тока, протекающего по
резистору, на величину сопротивления
этого резистора.
В
электротехнике разность потенциалов
на концах резистора принято называть
либо «напряжением на резисторе», либо
«падением напряжения». В литературе
встречаются оба этих определения.
Рассмотрим
теперь вопрос о напряжении на участке
цепи, содержащем не только резистор, но
и источник ЭДС.
На
рис. 1-14 а
и б
показаны участки некоторых цепей, по
которым протекает ток ..
Найдем напряжение между точками a
и c
для этих участков.
а)
б)
Рис.
1-14. Участки электрической цепи
По
определению
.
(1-9)
Выразим
потенциал точки a
через потенциал точки c.
При перемещении от точки c
к точке b
(рис. 1-14,а)
идем встречно ЭДС ,
поэтому потенциал точки b
оказывается меньше, чем потенциал точки
c
на величину ЭДС ,
т.е.
.
(1-10)
На
рис. 1-14,б
при перемещении от точки c
к точке b
идем согласно ЭДС
и потому потенциал точки b
оказывается больше, чем потенциал точки
c
на величину ЭДС ,
т.е.
.
(1-11)
Ранее
говорилось, что на участке цепи без ЭДС
ток течет от более высокого потенциала
к более низкому. Поэтому в обеих схемах
рис. 1-14 потенциал точки a
выше, чем потенциал точки b
на величину падения напряжения на
резисторе сопротивлением :
. (1-12)
Таким
образом, для рис. 1-14,а
имеем
,
или
.
(1-13)
И
для рис. 1-14, б
имеем
,
или
.
(1-14)
Положительное
направление напряжения указывают на
схемах стрелкой. Стрелка должна быть
направлена от первой буквы индекса ко
второй. Так, положительное направление
напряжения
изобразится
стрелкой, направленной от a
к c.
Из
самого определения напряжения следует
также, что .
Поэтому .
Другими словами, изменение чередования
индексов равносильно изменению знака
этого напряжения. Из изложенного ясно,
что напряжение может быть и положительной,
и отрицательной величиной.
Закон
Ома устанавливает связь между током и
напряжением на некотором участке цепи.
Так, применительно к участку цепи,
изображенному на рис. 1-13 имеем
или
.(1-15)
Сопротивление
Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.
Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.
Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.
Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.
Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.
Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала.
Эту закономерность можно описать следующей формулой:
Сопротивление R = ρ · l/S R — сопротивление l — длина проводника S — площадь поперечного сечения ρ — удельное сопротивление [Ом · мм2/м] |
Единица измерения сопротивления — ом. Названа в честь физика Георга Ома.
Будьте внимательны!
Площадь поперечного сечения проводника и удельное сопротивление содержат в своих единицах измерения мм2. В таблице удельное сопротивление всегда дается в такой размерности, да и тонкий проводник проще измерять в мм2. При умножении мм2 сокращаются и мы получаем величину в СИ.
Но это не отменяет того, что каждую задачу нужно проверять на то, что там мм2 в обеих величинах! Если это не так, то нужно свести не соответствующую величину к мм2.
Знайте!
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
Удельное сопротивление проводника — это физическая величина, которая показывает способность материала пропускать электрический ток. Это табличная величина, она зависит только от материала.
Как узнать напряжение, зная силу тока?
Снова поговорим о постоянном напряжении. Напряжение – это сила, действующая на заряженные частицы, заставляющая их двигаться. Вернемся к реке. Даже если она будет широкой и глубокой, но вода в ней не будет двигаться, она не сможет совершать какую-то работу. Движение воды происходит из-за перепада уровней поверхности земли. Чем больше разница между уровнями дна на каком-то участке, тем быстрее будет поток, и тем большую работу может совершать вода.
Напряжение в каком-то смысле можно сравнить с таким перепадом: чем выше напряжение при одном и том же токе, тем большей мощностью обладает энергия, проходящая по проводнику. При постоянном напряжении электроны движутся всегда в одном направлении, но существуют более сложные схемы изменения напряжения или тока:
- переменный;
- периодический;
- синусоидальный;
- квазистационарный;
- высокочастотный;
- пульсирующий;
- однонаправленный.
Эти разновидности часто сопутствуют друг другу. Так в домашней сети применяются сразу три разновидности: переменный, периодический, синусоидальный. Переменное напряжение указывает на противоположные знаки напряжения в течение одного периода. Происходит это следующим образом: напряжение от ноля поднимается до максимального положительного значения, затем опускается до ноля и опускается до максимального отрицательного значения. Поскольку такие изменения происходят за равный промежуток времени, их называют периодическими. Плавные переходы носят синусоидальный вид, что соответствует названию такого тока.
Переменное напряжение может быть:
- однофазным;
- двухфазным;
- трехфазным.
В первом случае есть фазный и нулевой провод. При подключении нагрузки электроны движутся то в одном направлении, то в другом. Чтобы определить соотношение напряжения и мощности в переменном токе используют среднеквадратическое значение. Оно определяется по нагреванию нагрузки одного и того же номинала. Сначала пропускают постоянный ток одного напряжения в течение определенного времени и замеряют температуру нагрева испытуемого тела. Затем опытным путем подбирают такое переменное напряжение, при котором за то же время происходит такое же нагревание.
Для однофазного переменного тока оно будет меньше в от амплитудного значения. То есть в сети вольтметр показывает 220 В среднеквадратическое значение, а амплитудное будет составлять 311 В.
Двухфазный ток может быть либо сдвинутым, как, например, взятые две фазы у трехфазной сети, либо противоположным. В последнем случае фазы работают таким образом, что максимальное положительное значение одной фазы, соответствует максимальному отрицательному значению другой.
Для создания вращающегося магнитного поля применяют трехфазную сеть. Обычно к ней подключают электродвигатели. Если обмотки соединены по схеме треугольника, то суммарная мощность каждой фазы будет равна линейной. При подключении по схеме звезда суммарная мощность будет в больше линейной. Схема подключения электродвигателя указана на его шильдике (табличке).
Определение напряжения при известном токе и мощности, осуществляется по той же формуле. Если определяется трехфазное напряжение, то следует учитывать схему подключения нагрузки и добавлять или нет коэффициент .
Закон Ома — формула
Формула закона Ома может быть использована, когда известно две из трех переменных. Соотношение между сопротивлением, током и напряжением может быть записано по-разному. Для усвоения и запоминания может быть полезен «треугольник Ома».
или
или
Ниже приведены два примера использования такого треугольного калькулятора.
| Имеем резистор сопротивлением в 1 Ом в цепи с падением напряжения от 100В до 10В на своих выводах.Какой ток протекает через этот резистор?Треугольник напоминает нам, что: | |
| Имеем резистор сопротивлением в 10 Ом через который протекает ток в 2 Ампера при напряжении 120В.Какое будет падение напряжения на этом резисторе?Использование треугольника показывает нам, что:Таким образом, напряжение на выводе будет 120-20 = 100 В. |
Закон Ома для участка цепи
С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит. Чем сильнее качаем, тем больше течение. В электрической цепи функцию насоса выполняет источник тока.
Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. В результате этих реакций выделяется энергия, которая потом передается электрической цепи.
У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «−».
У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.
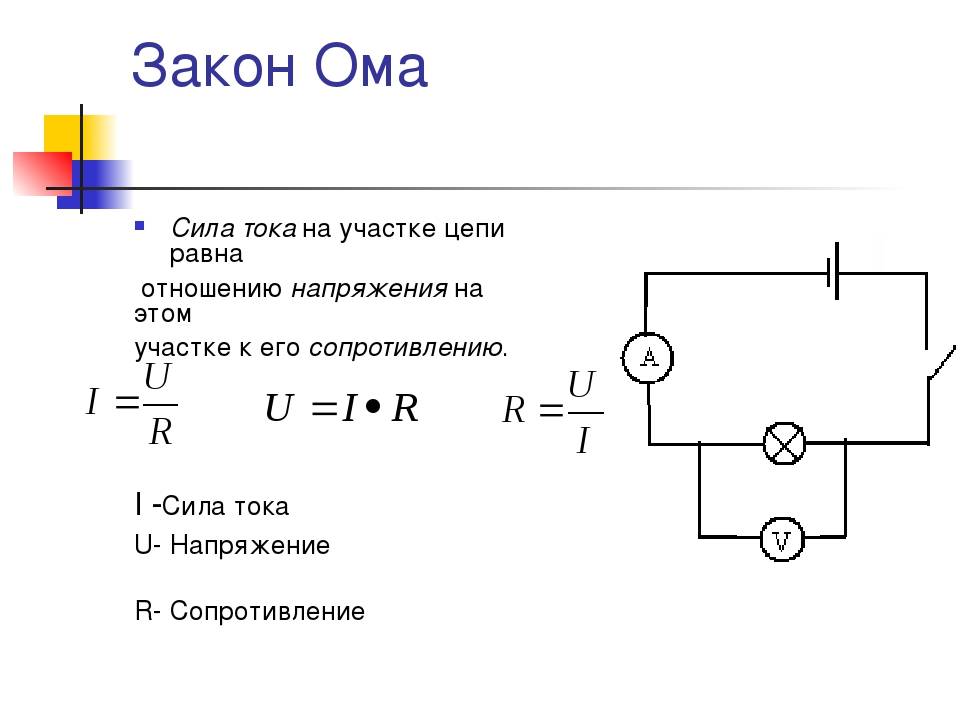
Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.
Математически его можно описать вот так:
Закон Ома для участка цепи I = U/R I — сила тока U — напряжение R — сопротивление |
Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.
Сила тока измеряется в амперах, а подробнее о ней вы можете прочитать в нашей статье.
Давайте решим несколько задач на закон Ома для участка цепи.
Задача раз
Найти силу тока в лампочке накаливания торшера, если его включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом.
Решение:
Возьмем закон Ома для участка цепи:
I = U/R
Подставим значения:
I = 220/880 = 0,25 А
Ответ: сила тока, проходящего через лампочку, равна 0,25 А
Давайте усложним задачу. И найдем силу тока, зная все параметры для вычисления сопротивления и напряжение.
Задача два
Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а длина нити накаливания равна 0,5 м, площадь поперечного сечения 0,01 мм2, а удельное сопротивление нити равно 1,05 Ом · мм2/м.
Решение:
Сначала найдем сопротивление проводника.
R = ρ · l/S
Площадь дана в мм2, а удельное сопротивления тоже содержит мм2 в размерности.
Это значит, что все величины уже даны в СИ и перевод не требуется:
R = 1,05 · 0,5/0,01 = 52,5 Ом
Теперь возьмем закон Ома для участка цепи:
I = U/R
Подставим значения:
I = 220/52,5 ≃ 4,2 А
Ответ: сила тока, проходящего через лампочку, приблизительно равна 4,2 А
А теперь совсем усложним! Определим материал, из которого изготовлена нить накаливания.
Задача три
Из какого материала изготовлена нить накаливания лампочки, если настольная лампа включена в сеть напряжением 220 В, длина нити равна 0,5 м, площадь ее поперечного сечения равна 0,01 мм2, а сила тока в цепи — 8,8 А
Решение:
Возьмем закон Ома для участка цепи и выразим из него сопротивление:
I = U/R
R = U/I
Подставим значения и найдем сопротивление нити:
R = 220/8,8 = 25 Ом
Теперь возьмем формулу сопротивления и выразим из нее удельное сопротивление материала:
R = ρ · l/S
ρ = RS/l
Подставим значения и получим:
ρ = 25 · 0,01/0,5 = 0,5 Ом · мм2/м
Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.
Ответ: нить накаливания сделана из константана.