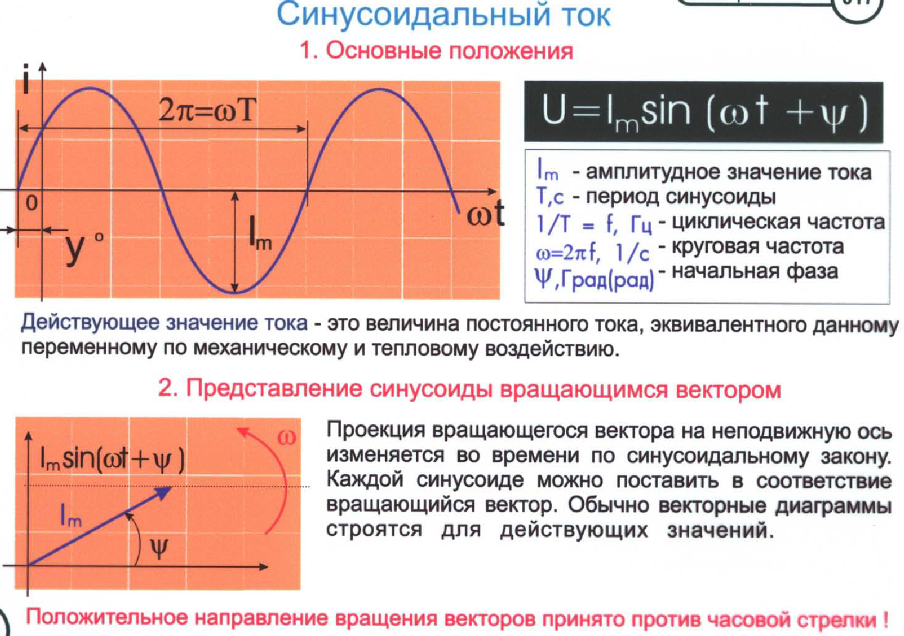
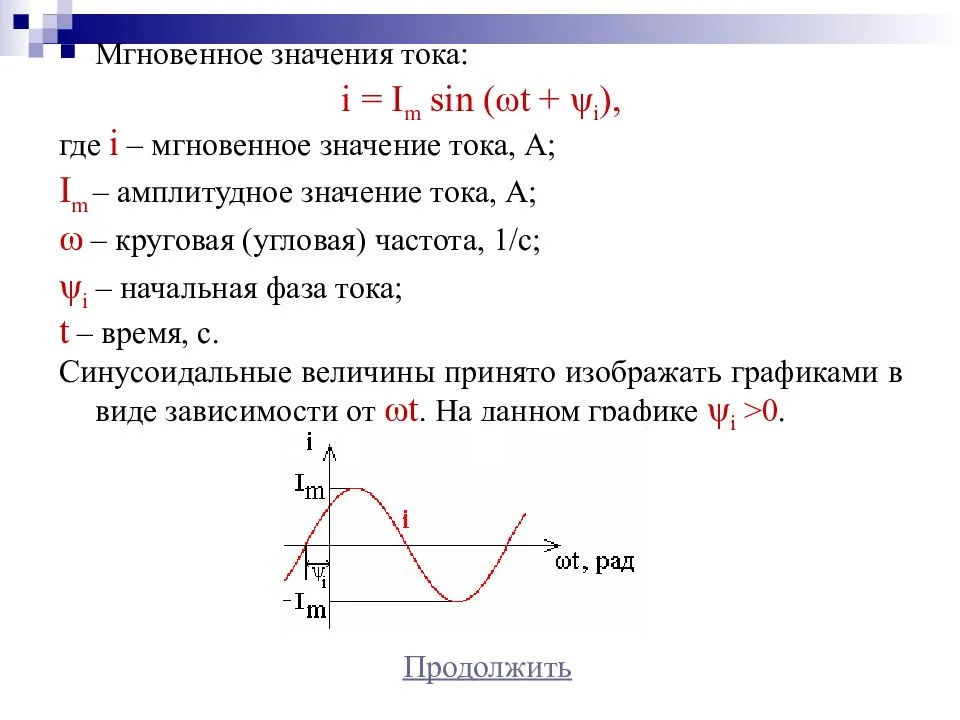
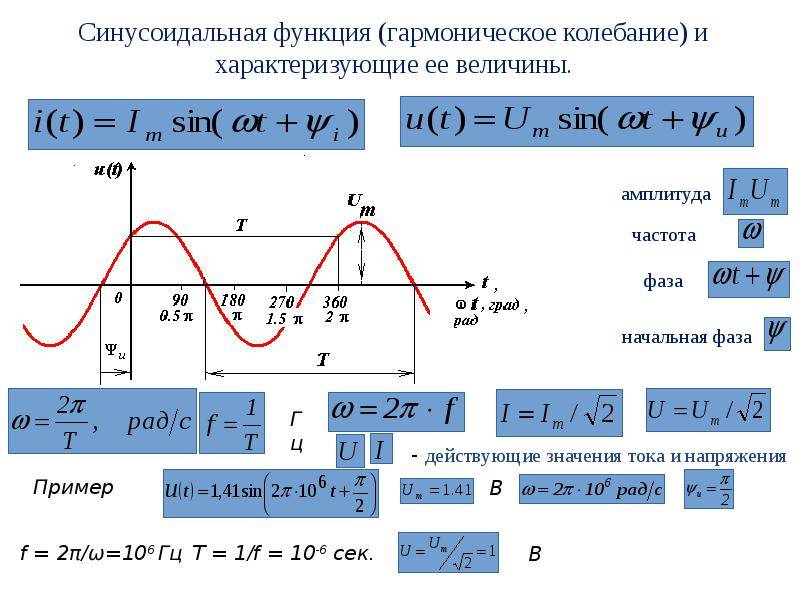
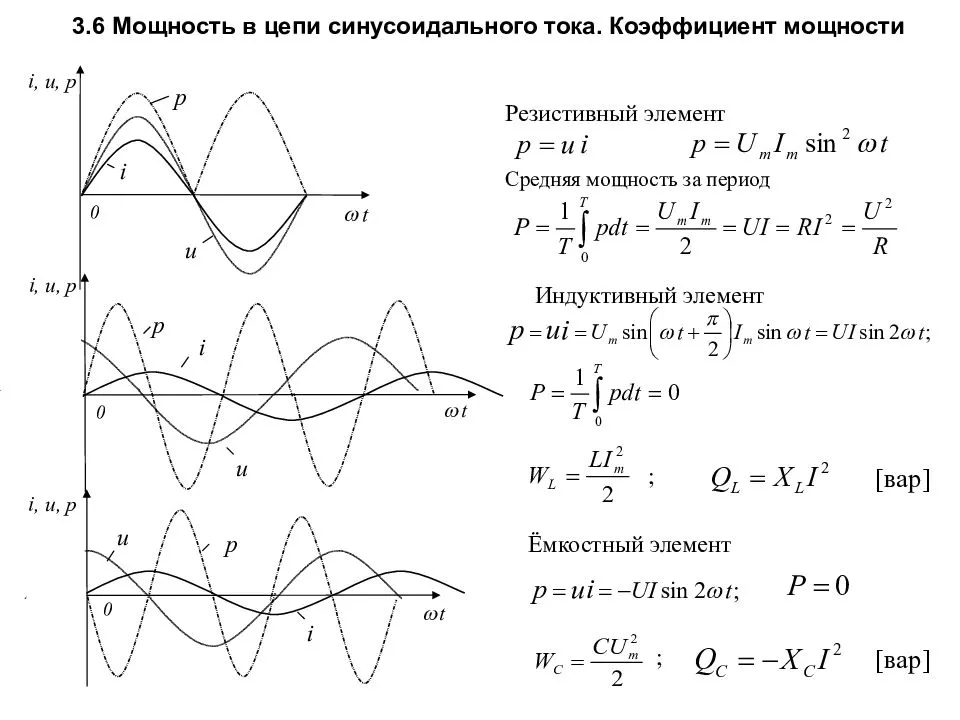
Векторное изображение синусоидально изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е1 и е2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток
Каждый из этих токов синусоидален и может быть представлен уравнением
Результирующий ток также будет синусоидален:

Определение амплитуды
t=0.w
Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
Построение векторной диаграммы в масштабе позволяет определить значения
«>
ⓘ Энциклопедия | Угловая частота — Вики ..
Исследование частотных характеристик дросселей в широком.
Local offer Физика длина скорость волна. check волновое число. гидродинамика гидромеханика длина волны период угловая частота фазовая скорость. 2.1. Спектры периодических сигналов. Кая круговая частота колебаний, δ – начальная фаза колебаний. кие колебания с циклической частотой ω. V, угловая скорость ω и радиус враще. Циклическая частота. Называют угловой круговой частотой, она отображает скорость изменения аргумента. Угловая частота измеряется в рад с. Значение фазы при. 0. t. Занятие 9. Цепи синусоидального тока. Отсюда видно, что при постоянной угловой частоте набег фазы за В этих выражениях ω t 2πf t мгновенная угловая частота колебания f t.
ГОСТ ИСО 10112 2002 Материалы.
Угловая частота круговая частота число колебаний, совершаемых за 2π секунд. Угловой частоты, где ν число колебаний в секунду, Т период. Угловая частота с видео 2. Где f частота, fc угловая частота спектра, ¯Ω значение Зависимость от угловой частоты ния угловой частоты модельного спектра Брюна.
Метод многоядерной МРТ Хабр Habr.
Ω, угловая частота, измеряется в радианах в секунду. Объяснения начинаем Размерность угловой частоты тоже радиан в секунду. Круговая частота. Циклическая частота Обучение Интернет. УГЛОВАЯ ЧАСТОТА. УГЛОВАЯ ЧАСТОТА круговая частота, число колебаний, совершаемое за 2p секунд. Угловая частота w 2pn 2p T, где n число.
Radian: перевод, произношение, транскрипция WooordHunt.
В системе СИ выражается в герцах Гц. Период и частота колебаний связаны соотношением: Циклическая или круговая частота ω 2πν. Она связана с. Слова на букву У Угловая минута секунда скорость мгновенная. Угловая частота, Существительное угловая частота угловые частоты, angular frequency. УГЛОВАЯ ЧАСТОТА Современная Энциклопедия Словари. Угловая частота, круговая частота, число полных колебаний, совершающихся при периодическом колебательном процессе за 2p единиц времени. Угловая частота гармонических колебаний вибрации. Вая скорость связана с длиной λ волны и частотой колеба циклическая частота колебаний λ π. 2 8. ω0 – угловая частота колебаний маятника. Калькулятор импеданса последовательной LC цепи. Угловая циклическая частота переменного тока. Скорость вращения радиуса вектора, т. е. изменение величины угла поворота в течение одной.
Угловая частота Мегаэнциклопедия Кирилла и Мефодия.
Угловая частота. фаза. мгновенное значение. ВЛЭП. Далее рассмотрим все эти. Cheb2ap Документация MATLAB. Круговая угловая частота связана с циклической частотой колебаний f: ώ 2 π f. Циклическая частота f связана с периодом колебаний Т соотношением:. Угловая частота перевод с русского на английский. Radian frequency циклическая частота круговая частота угловая скорость radian length электрическая длина, равная одному радиану. Периодические синусоидальные сигналы. Ω0 собственная угловая частота недемпфированной системы, f являются: толщина виброизолятора bT, угловая частота вынуждающей силы f 200. Скачать ГОСТ 24346 80 Вибрация. Термины и определения. Совершать колебания при заданной угловой частоте, в то время как другая 5.5 Точность измерения величины угловой частоты должна составлять ±2.
Греческий алфавит и физические величины.
Эту величину называют частотой излучения ν. Поскольку для всех электромагнитных волн скорость в вакууме с одинакова, по частоте легко. 3.4. Угловая модуляция. Фаза и мгновенная частота колебания. Ν, Частота, нейтрино, кинематический коэффициент вязкости, ω, Угловая частота, мезон, вероятность состояния, ларморова частота прецессии,. УГЛОВАЯ ЧАСТОТА это Что такое УГЛОВАЯ ЧАСТОТА?. Где ω 0 ларморова угловая частота прецессии ядра,.
Параметры переменного тока и напряжения
Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:
ПериодT — время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.
Частотаf — величина, обратная периоду, равная количеству периодов за одну секунду. Один период в секунду это один герц (1 Hz)
Циклическая частотаω — угловая частота, равная количеству периодов за2π секунд.
Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°
Начальная фазаψ — величина угла от нуля (ωt = 0) до начала периода. Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.
Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.
Мгновенное значение
— величина напряжения или тока измеренная относительно нуля в любой выбранный момент времениt .
Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени. Например, синусоидальный ток или напряжение можно выразить функцией:
i = I ampsin(ωt); u = U ampsin(ωt)
С учётом начальной фазы:
i = I ampsin(ωt + ψ); u = U ampsin(ωt + ψ)
Здесь I amp
иU amp — амплитудные значения тока и напряжения.
Что такое среднее значение переменного напряжения?
Ещё одним параметром переменного напряжения, который его характеризует, является средним значением переменного напряжения. В отличие от действующего значения переменного напряжения, которое характеризует работу переменного напряжения, среднее значение напряжения характеризует количество электричества, которое перемещается из одной точки цепи в другую, под действием переменного напряжения. Среднее значение напряжения за период определяется следующим выражением
где Т – период переменного напряжения,
fu(t) – функциональная зависимость напряжения от времени.
Таким образом, среднее значение переменного напряжения численно будет равно высоте прямоугольника с основанием T, площадь которого равна площади, ограниченной функцией fu(t) и осью Ox за период Т.

Среднее значение переменного напряжения.
В случае синусоидальной функции, можно говорить только о среднем значении за полупериод, так как в течение всего периода положительная полуволна компенсируется отрицательной полуволной, и тогда среднее за период напряжение будет равно нулю.
Таким образом, среднее за полупериод Т/2 значение переменного напряжения синусоидальной формы будет равно

где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла).
Примеры резонанса
Если влажный палец двигать по краю бокала, то бокал будет издавать звенящие звуки. Хотя это и незаметно, палец движется прерывисто и передает стеклу энергию короткими порциями, заставляя бокал вибрировать
Стенки бокала также начинают вибрировать, если на него направить звуковую волну с частотой, равной его собственной. Если амплитуда станет очень большой, то бокал может даже разбиться. По причине резонанса при пении Ф.И.Шаляпина дрожали (резонировали) хрустальные подвески люстр. Возникновение резонанса можно проследить и в ванной комнате. Если вы будете негромко пропевать звуки разной частоты, то на одной из частот возникнет резонанс.
В музыкальных инструментах роль резонаторов выполняют части их корпусов. Человек также имеет собственный резонатор — это полость рта, усиливающая издаваемые звуки.
Явление резонанса необходимо учитывать на практике. В одних явлениях он может быть полезен, в других — вреден. Резонансные явления могут вызывать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США.
Явление резонанса используется, когда с помощью небольшой силы необходимо получить большое увеличение амплитуды колебаний. Например, тяжелый язык большого колокола можно раскачать, действуя сравнительно небольшой силой с частотой, равной собственной частоте колебаний колокола.
Мгновенная мощность в цепи переменного тока с активным сопротивлением.
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = Umsinωt * Imsinωt = UmImsin2ωt
Из тригонометрии найдём
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р = UmIm√2 и перемен- ной р’:
р = Р + р’
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
СИНУСОИДАЛЬНЫЕ ВЕЛИЧИНЫ И ИХ ИЗОБРАЖЕНИЯ
В электротехнике России используют синусоидальный переменный ток частотой 50 Гц. Частота — это число колебаний переменной величины в одну секунду. Синусоидальную форму тока и напряжения удобно получать и использовать в электрических машинах (генераторах и двигателях). При синусоидальной форме тока в нем отсутствуют составляющие других частот (гармоники), создающие дополнительные потери в электрических машинах.
Математически синусоидальные величины записывают в следующем виде: напряжение u = Um sin (ωt + φu), ток i = Im sin (ωt + φu – φ).
В указанных выражениях: u, i — мгновенные значения напряжения и тока (т. е. значения в данный момент времени t); Um, Im — наибольшие значения (амплитуды); ω — угловая частота; φu — начальная фаза напряжения; φ — сдвиг по фазе тока относительно напряжения; значения (ωt + φu), (ωt + φu – φ) называют фазами напряжения и тока. Фаза — величина, определяющая состояние колебательного процесса в каждый момент времени. Мгновенные значения обозначают строчными латинскими буквами u, i.
Наиболее простое графическое изображение синусоидальных величин получается в виде временной диаграммы (рис. 1).
Рис. 1. Временные диаграммы тока и напряжения
На рис. 1 начальная фаза напряжения принята φu = 0 с целью упрощения. Ток в фазе отстает от напряжения на угол φ ≈ 45°, т. е. u = Um sin ωt; i = Im sin (ωt – 45°). Отстающий угол φ откладывается от начала координат вправо по оси времени t. На первый взгляд может показаться, что на рис. 1 ток i опережает по фазе напряжение и, т. к. он смещен по оси времени t вправо (как бы бежит впереди напряжения). Противоречие устраняется, если рассмотреть моменты переходов через нуль тока и напряжения: ток пересекает ось времени t позже, чем напряжение.
Обычно потребители работают с отрицательным φ (φ < 0), т. е. с отстающим по фазе током.
Амплитудные (наибольшие мгновенные на данном периоде) значения синусоидальных величин обозначают +Um, -Um; +Im, -Im, в зависимости от знака напряжения или тока (положительный или отрицательный).
Интервал времени, за который величина совершает полное колебание, т. е. после которого форма повторяется, называют периодом колебания Т.
Частота тока измеряется в герцах, Гц.
1 Гц соответствует одному колебанию в секунду.
При f = 50 Гц Т = 0,02 с или 20 миллисекунд (мс).
Угловая частота ω связана с частотой в соответствии с выражением ω = 2πf, 1/с, где π ≈ 3,14. При f = 50 Гц ω = 314 1/с.
Более абстрактное изображение синусоидальных величин получается с помощью векторов на комплексной плоскости.
Из математики известно, что существуют действительные и мнимые числа. Мнимым числом называют величину, получаемую после извлечения квадратного корня из отрицательного числа. Если на плоскости провести две взаимно перпендикулярные оси, одна из которых соответствует действительному числу, а другая — мнимому, то точки плоскости будут представлять собой комплексные числа, а плоскость будет называться комплексной. Комплексную плоскость разбивают осями координат на 4 части (квадранта). Ось +1 — вещественная или действительная ось. Ось +j — мнимая ось. Точка 0 — начало координат. Синусоидальные токи и напряжения изображают в виде вращающихся против часовой стрелки с угловой частотой ω векторов Úm , Ím , длины (модули) которых равны амплитудам Im, Um. Векторы удобно строить для момента времени t = 0.
Рис. 2. Векторные диаграммы тока и напряжения
Как рассчитать синусоидальные волны?
Для выполнения вычислений с использованием синусоидальных волн используется научный калькулятор, который имеет тригонометрические функции синуса и косинуса, а также их обратные. В этих калькуляторах есть режимы для работы с углами в градусах или радианах, и их легко преобразовать из одной формы в другую. Коэффициент преобразования:
180 º = π радианы.
В зависимости от модели калькулятора, вы должны перемещаться с помощью клавиши MODE, чтобы найти опцию DEGREE, которая позволяет вам работать с тригонометрическими функциями в градусах, или опцию RAD, чтобы напрямую работать с углами в радианах.
Например, sin 25º = 0,4226 при установке калькулятора в режим DEG. Преобразование 25º в радианы дает 0,4363 радиана, а sin 0,4363 рад = 0,425889 ≈ 0,4226.
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).

Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мс =0,001сек =10 -3 сек.
1 мкс=0,001 мс = 0,000001сек =10 -6 сек.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
Что такое амплитуда
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина \( \large x \). Тогда символом \( \large x_{0} \) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
 Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Ответ
Проверено экспертом
Речь идём о переменном токе.
Мгновенное значение (ЭДС или напряжения или тока) — значение величины в данный момент времени. обозначается чаще всего маленькими буквами: e, u,i.
Амплитудное значение (ЭДС или напряжения или тока) — максимальное значение. Обозначается :
Действующее значение отличается от максимального тем, что оно меньше максимального в раз, т.е.( на примере тока, для напряжения и ЭДС аналогично):
Обозначается действующее значение или без иднекса или с индексом «д»:
(только русское «д»).
Смысл действующего значения: при переменном токе (i) за период выделиться столько же тепла, сколько выделиться при действующем значении
Имеено действующее значение показывают приборы, подключённые в цепь с переменным током.
Среднее значение величин (-//-) -среднее арифметическое значение величины за полпериода.
Максимальным значением (амплитудой) тока и напряжения называется та наибольшая величина, которой они достигают за один период. Максимальное значение тока и напряжения обозначается: напряжения — Um, тока — Im.
Величину переменной силы тока и напряжения для любого произвольного момента времени называют мгновенным значением этой величины. Обозначают мгновенные значения переменных величин строчными буквами латинского алфавита, например, электрического тока и электрического напряжения i и u соответственно.
Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.
Если ток изменяется по закону синуса, т. е.

то действующее значение переменного тока, обозначаемое также, как и значение постоянного тока заглавной буквой I латинского алфавита, определится как:
.
Аналогично для действующих значений синусоидальных напряжений:
.
Фаза. Сдвиг фаз.
Пусть на якоре генератора укреплены два одинаковых витка 1 и 2, сдвинутых в пространстве на угол φ. При вращении якоря в витках наводится ЭДС индукции одинаковой частоты ω и амплитуды Em, так как витки вращаются с одинаковой частотой в одном и том же магнитном поле.
Положение витков задано углами ψ1 и ψ2 для произвольного момента времени, которое можно считать t = 0. Мгновенные значения ЭДС как функции времени определяются выражениями:
Следовательно, в момент t = 0 значения обеих этих ЭДС отличны от нуля:
Электрические углы ψ1 и ψ2 характеризуют значения ЭДС в начальный момент времени и называются начальными фазами.
Сдвиг фаз — это разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой.
Дата добавления: 2016-05-25 ; просмотров: 7354 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:
Аналогично определяются действующие значения ЭДС и напряжения.
Формы представления синусоидальных электрических величин.
Любая, синусоидально изменяющаяся, электрическая величина (ток, напряжение, ЭДС) может быть представлена в аналитическом, графическом и комплексном видах.
1). Аналитическая форма представления
I = Im·sin(ω·t + ψi), u = Um·sin(ω·t + ψu), e = Em·sin(ω·t + ψe),
где I, u, e – мгновенное значение синусоидального тока, напряжения, ЭДС, т. е. Значения в рассматриваемый момент времени;
Im, Um, Em – амплитуды синусоидального тока, напряжения, ЭДС;
(ω·t + ψ) – фазовый угол, фаза; ω = 2·π/Т – угловая частота, характеризующая скорость изменения фазы;
ψi, ψu, ψe – начальные фазы тока, напряжения, ЭДС отсчитываются от точки перехода синусоидальной функции через нуль к положительному значению до начала отсчета времени (t = 0). Начальная фаза может иметь как положительное так и отрицательное значение.
Какие токи бывают
Для питания электрических устройств и электротехники необходима энергия. Постоянный и переменный токи являются способом передачи энергии из одной точки в другую с использованием проводников.
Важно! Основное различие между ними заключается в характере движения заряженных частиц. Постоянный ток течет равномерно в одном направлении, в то время, как переменный постоянно изменяет направление с заданной скоростью или частотой
Основным следствием этого является полярность напряжения.
Постоянный
Постоянный ток характеризуется неизменным показателем полярности заряженных частиц
Поскольку постоянный ток сохраняет постоянную полярность, важно обращать внимание на то, как подключается устройством – неверное подключение устройства к сети с большой долей вероятности выедет его из строя. Хорошим примером являются устройства с автономным питанием от аккумуляторов – на них всегда наносятся обозначения для их корректного подключения. В противном случае, техника просто не заработает, так как не получит электропитания
В противном случае, техника просто не заработает, так как не получит электропитания.
Важно! При использовании постоянного тока, показатель напряжения может сильно разниться, в зависимости от используемого устройства. Типовые значения номинального напряжения автономных источников питания составляют 1.5V, 3.7V, 6V, 9V,12V, 24V и т.д
Вам это будет интересно На какую мощность рассчитан автомат 16а
Изменение направления тока
Переменный
С переменным током полярность постоянно переключается между положительным и отрицательным значениями. При подобной характеристике силового поля напряжение будет постоянно меняться, а полярность в таком случае не оказывает никакого влияния на работоспособность сети. Именно поэтому, любое бытовое электрическое устройство можно включать в сеть, не задумываясь о положении вилки в розетке, то есть, о соблюдении корректной полярности.
Основной причиной широкого распространения переменного тока является относительная легкость и эффективность в увеличении, либо уменьшении напряжения. Это достигается с помощью трансформаторов, а количество изменений количественных показателей определяется числом обмоток.
Важно! Такая же трансформация допускается и для постоянной величины, но это явление не является эффективным для его применения на практике. Также, это является еще одной, дополнительной причиной, по которой в бытовой сети используется именно переменный ток
Фазы в батарейке
Несмотря на то, что более низкие напряжения легче генерировать, высокие показатели несут меньшие потери при их передаче на расстояния. Поэтому перед подачей потребителям переменное напряжение повышается до нескольких сотен киловольт. Но, как только электричество достигает своего пункта назначения, оно снижается до 110 или 220 вольт. Дело в том, что переменный показатель имеет два установленных стандартных напряжения, которые используются во всем мире: 220В и 110В. Частота в электротехнике играет определяющее значение, и устройства, рассчитанные под напряжение в 110В, не станут работать от сети в 220В.