Электротехника метод контурных токов это

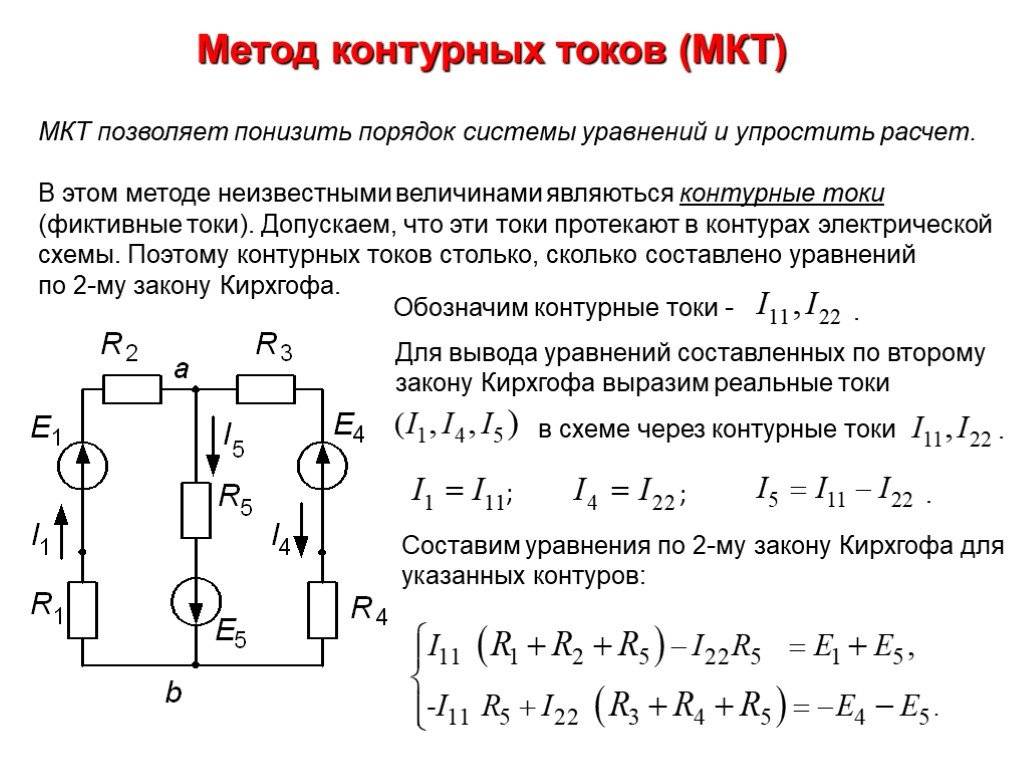
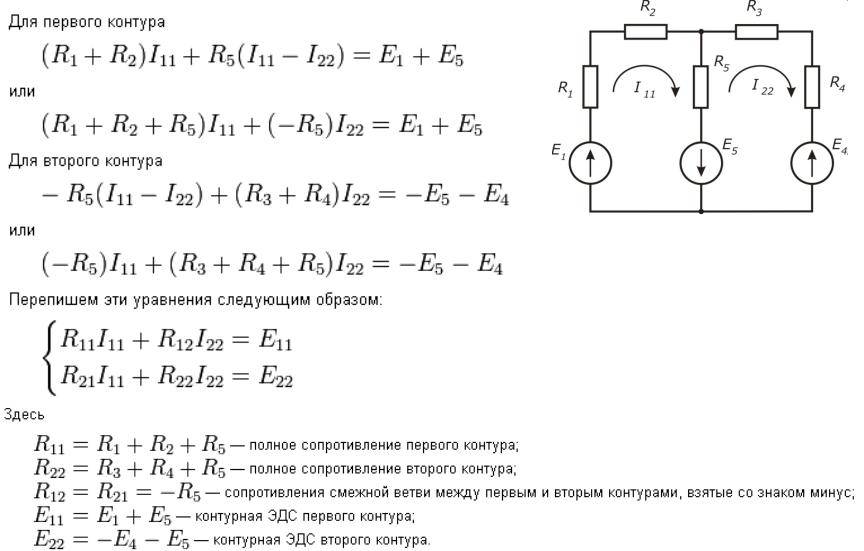
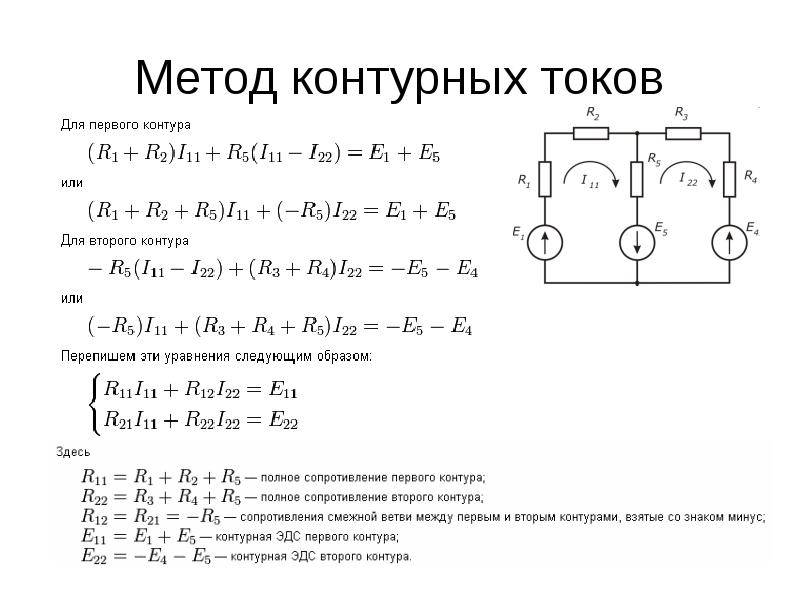
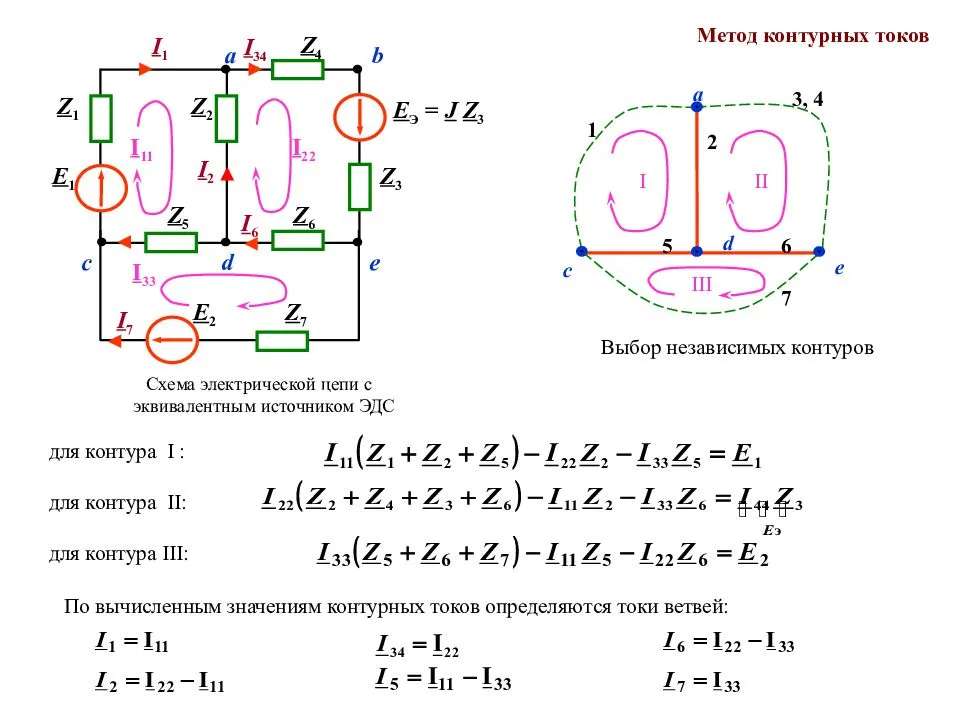
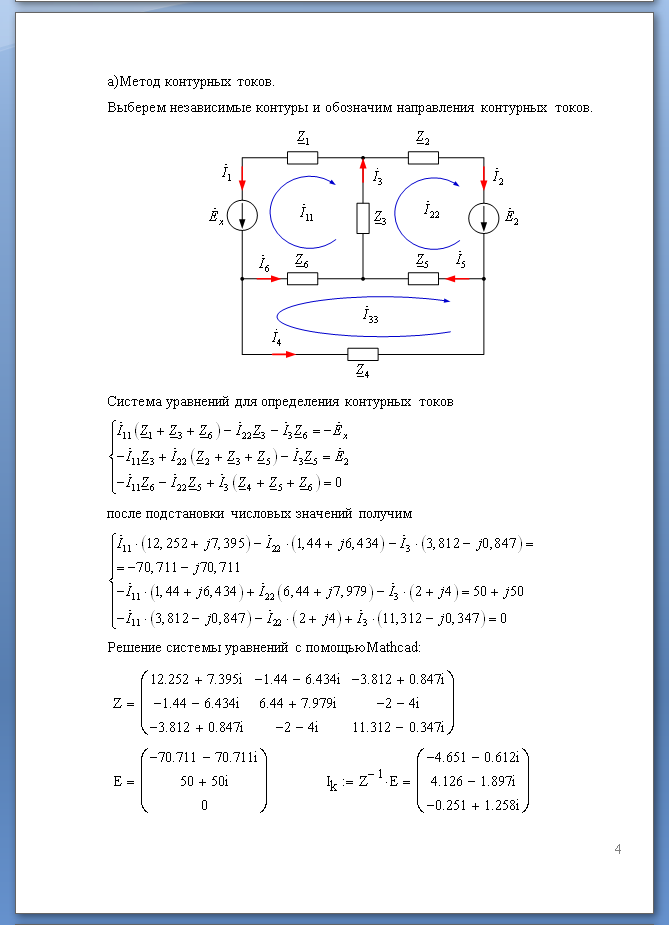
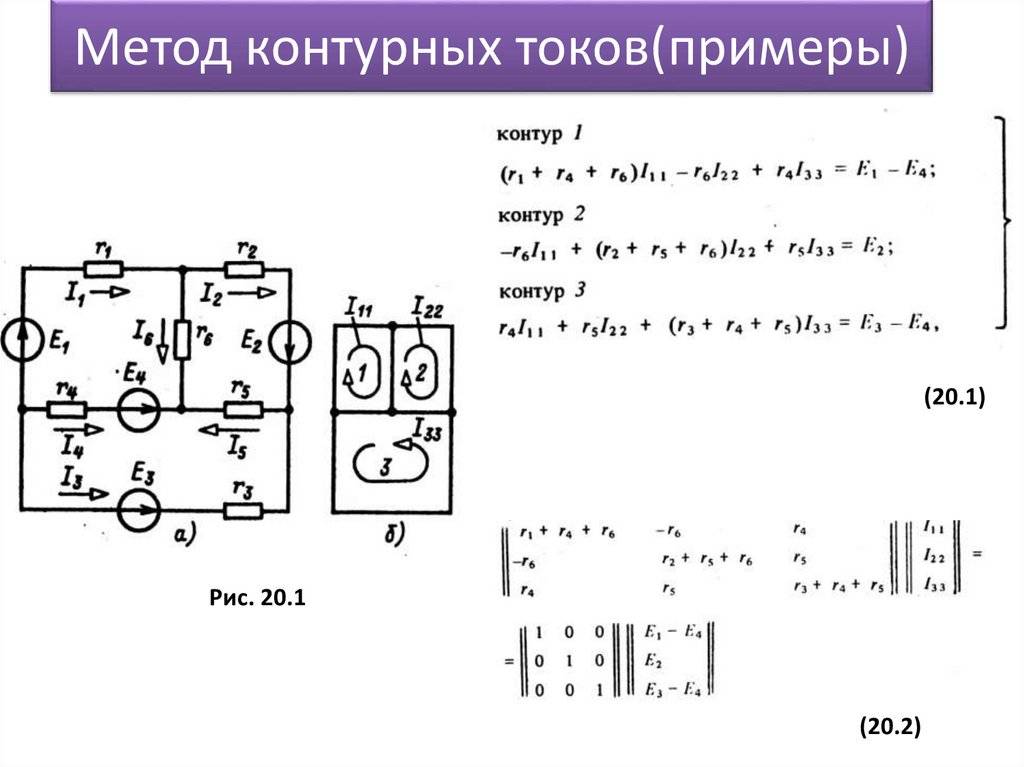
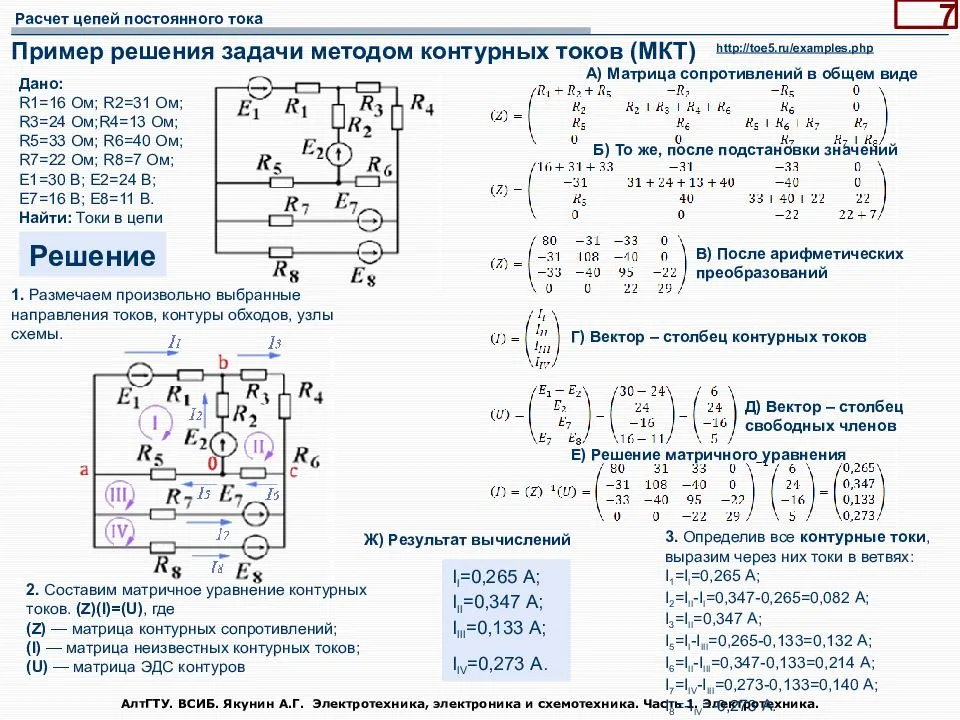
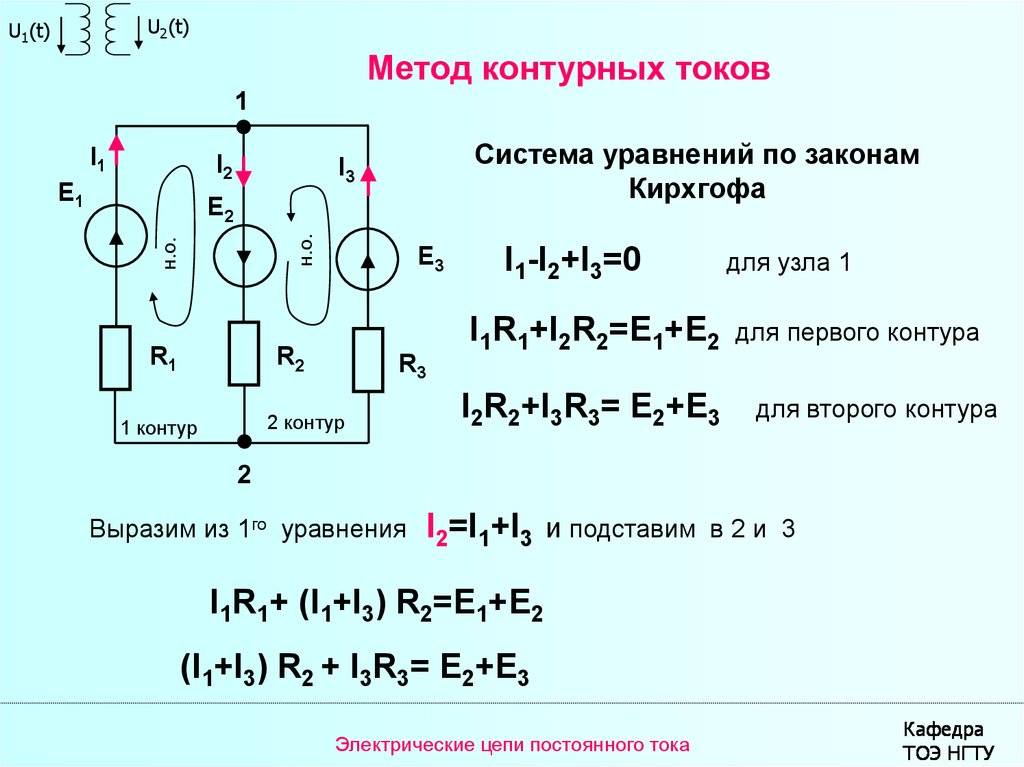
Метод узловых потенциалов для анализа электрической цепи синусоидального тока

Данный метод вытекает из первого закона Кирхгофа. В качестве неизвестных принимаются потенциалы узлов, по найденным значениям которых с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно , т.е. числу ветвей.

Метод узловых потенциалов, как и метод контурных токов является одним из основных расчетных приемов. В тех случаях, когда число узлов без единицы меньше числа независимых контуров в схеме, данный метод является более экономным, чем метод контурных токов.

Если схема имеет п узлов, то ей соответствует система из (n — 1) уравнений вида:

Проводимость в узле определяется как сумма проводимостей сходящихся ветвей:

— сумма проводимостей сходящихся в узле k. — сумма проводимостей ветвей, соединяющих узлы k и m, взятая со знаком минус.есть узловой ток k узла. Если к k узлу подтекает ток от источника тока, то он должен быть включен в ток Ikk со знаком плюс, если утекает, то со знаком минус. Если между какими-либо двумя узлами нет ветви, то соответствующая проводимость равна нулю.

После решения системы (1) относительно потенциалов определяют токи в ветвях по закону Ома для участка цепи, содержащего ЭДС.

Алгоритм

Заменить источники напряжения, включенные последовательно с сопротивлениями, на эквивалентные источники тока, включенные параллельно сопротивлениям.

Заменить сопротивления резисторов на проводимости.

Выбирать опорный узел (U0).

Назначить неизвестные напряжения (U1), (U2) … (UN) оставшимся узлам.

Сформировать уравнения Первого Закона Кирхгофа для каждого из узлов. Сумма проводимостей, связанных с первым узлом схемы, будет положительным коэффициентом первого напряжения в уравнении 1. Сумма проводимостей, связанных со вторым узлом схемы, будет положительным коэффициентом второго напряжения в уравнении 2, и так далее, в зависимости от количества узлов. В результате у вас должна получиться диагональ положительных значений.

Все остальные коэффициенты уравнений будут иметь отрицательный знак, так как они представляют проводимости, расположенные между узлами.

Правые части уравнений представляют собой значения источников тока, подключенных к соответствующим узлам.

Решитm систему уравнений, чтобы найти неизвестные напряжения.

Для узла а.

Подставим значения токов.

Сгруппируем соответствующие члены выражения.

Аналогично для узла b.

1. В левой части i-го уравнения записывается со знаком “+”потенциалi-го узла, для которого составляется данное i-е уравнение, умноженный на сумму проводимостейветвей, присоединенных к данному i-му узлу, и со знаком “-”потенциалсоседних узлов, каждый из которых умножен на сумму проводимостейветвей, присоединенных к i-му и k-му узлам.

Из сказанного следует, что все члены , стоящие на главной диагонали в левой части системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”, причем. Последнее равенство по аналогии с методом контурных токов обеспечивает симметрию коэффициентов уравнений относительно главной диагонали.

2. В правой части i-го уравнения записывается так называемый узловой ток , равный сумме произведений ЭДС ветвей, подходящих к i-му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i-му узлу, в противном случае ставится знак “-”. Если в подходящих к i-му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.

В заключение отметим, что выбор того или иного из рассмотренных методов определяется тем, что следует найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений. При расчете токов при одинаковом числе уравнений предпочтительнее использовать метод контурных токов, так как он не требует дополнительных вычислений с использованием закона Ома. Метод узловых потенциалов очень удобен при расчетах многофазных цепей, но не удобен при расчете цепей со взаимной индуктивностью.

Общий план составления уравнений

1 – Выбор направления действительных токов.

2 – Выбор независимых контуров и направления контурных токов в них.

3 – Определение собственных и общих сопротивлений контуров

4 – Составление уравнений и нахождение контурных токов

5 – Нахождение действительных токов

Итак, после ознакомления с теорией предлагаем приступить к практике! Рассмотрим пример.

Выполняем все поэтапно.

1. Произвольно выбираем направления действительных токов I1-I6.

2. Выделяем три контура, а затем указываем направление контурных токов I11,I22,I33. Мы выберем направление по часовой стрелке.

3. Определяем собственные сопротивления контуров. Для этого складываем сопротивления в каждом контуре.

Затем определяем общие сопротивления, общие сопротивления легко обнаружить, они принадлежат сразу нескольким контурам, например сопротивление R4 принадлежит контуру 1 и контуру 2. Поэтому для удобства обозначим такие сопротивления номерами контуров к которым они принадлежат.

4. Приступаем к основному этапу – составлению системы уравнений контурных токов. В левой части уравнений входят падения напряжений в контуре, а в правой ЭДС источников данного контура.

Так как контура у нас три, следовательно, система будет состоять из трех уравнений. Для первого контура уравнение будет выглядеть следующим образом:

Ток первого контура I11, умножаем на собственное сопротивление R11 этого же контура, а затем вычитаем ток I22, помноженный на общее сопротивление первого и второго контуров R21 и ток I33, помноженный на общее сопротивление первого и третьего контура R31. Данное выражение будет равняться ЭДС E1 этого контура. Значение ЭДС берем со знаком плюс, так как направление обхода (по часовой стрелке) совпадает с направление ЭДС, в противном случае нужно было бы брать со знаком минус.

Те же действия проделываем с двумя другими контурами и в итоге получаем систему:

В полученную систему подставляем уже известные значения сопротивлений и решаем её любым известным способом.

5. Последним этапом находим действительные токи, для этого нужно записать для них выражения.

Контурный ток равен действительному току, который принадлежит только этому контуру. То есть другими словами, если ток протекает только в одном контуре, то он равен контурному.

Но, нужно учитывать направление обхода, например, в нашем случае ток I2 не совпадает с направлением, поэтому берем его со знаком минус.

Токи, протекающие через общие сопротивления определяем как алгебраическую сумму контурных, учитывая направление обхода.

Например, через резистор R4 протекает ток I4, его направление совпадает с направлением обхода первого контура и противоположно направлению второго контура. Значит, для него выражение будет выглядеть

Метод узловых (потенциалов) напряжений

ТОЭ › Методы расчета цепей постоянного тока

При изучении основ электротехники приходится сталкиваться с необходимостью расчета тех или иных параметров различных схем. И самое простое, что приходится делать – это расчет токов ветвей в цепях постоянного тока.

Существует несколько наиболее применяемых методов расчетов для таких цепей: с помощью законов Кирхгофа, методом контурных токов, узловых потенциалов, методом эквивалентного генератора, эквивалентного источника тока, методом наложения. Для расчета более сложных цепей, например, в нелинейных схемах, могут применяться метод аппроксимации, графические методы и другие. В данном разделе рассмотрим один из методов определения токов в цепи постоянного тока – метод узловых потенциалов.

Важно отличать метод узловых напряжений (потенциалов) от метода узлового напряжения (метод двух узлов)

Метод узловых потенциалов примеры решения задач

Для того, чтобы лучше разобраться в этом вопросе, рассмотрим конкретный пример схемы, показанной на рис.1.

Рис.1. Схема постоянного тока

Для начала обозначают направления токов в ветвях. Направление можно выбирать любым. Если в результате вычислений какой-то из токов получится с отрицательным значением, значит, его направление в действительности будет направлено в противоположную сторону относительно ранее обозначенного. Если в ветви имеется источник, то для удобства лучше обозначить направление тока в этой ветви совпадающим с направлением источника в этой ветви, хотя и не обязательно. Далее один из узлов схемы заземляем. Заземленный узел будет называться опорным, или базисным. Такой метод заземления на общее токораспределение в схеме влияния не оказывает.

Какой именно узел заземлять, значения не имеет. Заземлим, например, узел 4 φ4 = 0.

Каждый из этих узлов будет обладать своим значением потенциала относительно узла 4. Именно значения этих потенциалов для дальнейшего определения токов и находят. Соответственно, для удобства этим потенциалам присваивают номера в соответствии с номером узла, т.е. φ1, φ2, φ3. Далее составляется система уравнений для оставшихся узлов 1, 2, 3.

В общем виде система имеет вид:

Использованные в этой системе уравнений буквенно-цифровые обозначения

имеют следующий смысл:

– сумма проводимостей ветвей, сходящихся в узле 1. В данном случае

– сумма проводимостей ветвей, сходящихся в узле 2. В данном случае

– сумма проводимостей ветвей, сходящихся в узле 3. В данном случае

– сумма проводимостей ветвей, соединяющих узлы 1 и 2, взятая со знаком «минус». Для этого единица и взята с отрицательным знаком:

– сумма проводимостей ветвей, соединяющих узлы 1 и 3, взятая со знаком «минус». Для этого единица и в этом случае взята с отрицательным знаком:

Аналогично находятся и остальные проводимости:

J11 – узловой ток узла 1, в котором участвуют ветви, подходящие именно к этому узлу, и содержащие в своем составе ЭДС. При этом, если ЭДС ветви, входящий в узел, направлена к рассматриваемому узлу (в данном случае к узлу 1), то такой узловой ток записывается с плюсом, если от узла, то с минусом. В данном случае

Аналогично

В результате всех ранее приведенных вычисленных значений исходная система уравнений примет вид:

Решать данную систему можно всеми доступными методами, мы же для упрощения решим ее в пакете Mathcad:

В результате получены следующие значения потенциалов в узлах цепи:

Токи в ветвях находятся в соответствии с законом Ома. Поясним это простыми словами.

В ветви с сопротивлением и источником, учитывая ранее обозначенное направление тока в рассматриваемой ветви, необходимо из потенциала узла, находящегося у начала стрелки направления тока, вычесть потенциал узла, находящегося у конца стрелки направления тока, а затем прибавить значение ЭДС в этой ветви. Далее все это разделить на сопротивление, имеющееся в ветви. Если бы ток и ЭДС в рассматриваемой ветви не совпадали по направлению, тогда значение ЭДС вычиталось. В ветви без ЭДС действует то же самое правило, только ЭДС в числителе, разумеется, отсутствует. В нашем примере получим, что

Значение тока первой ветви, как видно из расчета, получилось отрицательным. Значит, в действительности, этот ток направлен в противоположную сторону относительно его обозначенного направления на рис.1.

Правильность расчетов можно проверить, например, составлением баланса мощностей либо, к примеру, моделированием, схемы. Выполним моделирование в программе Multisim.

Рис.2. Моделирование в Multisim

Как видим, результаты моделирования совпадают с расчетными значениями. Незначительная разница в тысячных долях из-за округлений промежуточных вычислений.

Алгоритм расчета электрической цепи методом контурных токов

1. Вычерчиваем принципиальную схему цепи и обозначаем все элементы, задаем направления токов ветвей.

2. Определяем все независимые контуры.

3. Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры или римские цифры.

4. По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи уравнений учитывайте, что направление обхода цепи, из которого создаются уравнения, совпадает с направлением тока цепи в этой цепи. Необходимо учитывать тот факт, что в соседних ветвях, принадлежащих к двум цепям, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.

5. Решаем любым методом полученную систему относительно контурных токов и определяем их.

6. Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры

7. Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.

Возможно вам будут полезны данные страницы:

Расчет электрической цепи методом эквивалентных преобразований

Расчет электрической цепи по закону Кирхгофа

Расчет электрической цепи методом наложения

Метод двух узлов

Оптимизированная процедура составления системы

По упрощенной методике поступают следующим образом:

• В уравнениях в левой части записывают произведение суммы всех входящих в контур сопротивлений на контурный ток;
• От полученного выражения вычитаются умноженные на сумму сопротивлений общей ветви соседние контурные токи;
• Справа записывается сумма источников ЭДС контура.

Формальный подход

Формальный подход предполагает матричную форму записи системы уравнений. Для расчетов исходные данные записывают в матричной форме. Используются такие матрицы:

• C – в которой i строк, соответствующих количеству контуров, и j столбцов по количеству ветвей;
• Z – диагональная матрица сопротивлений, количество строк и столбцов которой соответствуют числу веток;
• Ct – транспонированная матрица С;
• I – матрица контурных величин;
• J – матрица источников тока;
• Е – матрица ЭДС.

При составлении матрицы С каждый элемент Сij

• 0, если ветвь j не входит в контур;
• -1, если ветвь входит в контур, направление тока противоположно контурному;
• 1 – то же самое, но направление тока совпадает с контурным.

В матрице Z диагональные элементы равняются сопротивлению участков, остальные приравниваются нулю.

Итоговая формула для расчетов имеет вид:

C∙Z∙Ct∙I=C(Z∙J+E).

Такая форма записи решения в матричной форме показывает, каким образом выполняются действия над составленными матрицами.

Пример системы уравнений

Ниже рассмотрен пример расчета конкретной схемы без учета номиналов элементов.

Пример решения

В заданной цепи выделяют три контура. Как выразить токи в ветвях через контурные:

• i1=I1;
• i2=I2;
• i3=I3;
• i4=I2+I3;
• i5=I1+I2;
• i6=I1-I3.

Как составить систему уравнений:

• i1R1+i5R5+i6R6=E1;
• i2R2+i4R4+i5R5=E2;
• i3R3+i4R4-i6R6=0

Как подставить контурные значения

• I1R1+( I1+I2)R5+( I1-I3)R6=E1;
• I2R2+( I2+I3)R4+( I1+I2)R5=E2;
• I3R3+( I2+I3)R4-( I1-I3)R6=0

После преобразования получается необходимая система уравнений:

• (R1+R5+R6)I1+R5I2+R6I3=E1;
• R5I1+(R2+R4+R5)I2+R4I3=E2;
• -R6I1+R4I2+(R3+R4+R6)I3=0.

Система из трех уравнений легко решается после подстановки известных параметров. Из полученных значений контурных токов затем можно найти искомые величины.

Данный пример решения задач по методу контурных токов показывает, что любую достаточно сложную схему можно существенно упростить для решения, руководствуясь указаниями.

Важно! Метод неприменим, если нет возможности преобразовать цепь без взаимного пересечения ветвей. В некоторых случаях упростить схему можно путем преобразования ветвей, соединенных по схеме «звезда» в треугольник

В некоторых случаях упростить схему можно путем преобразования ветвей, соединенных по схеме «звезда» в треугольник.

Точно такие же результаты получаются при использовании метода узловых потенциалов. В основе расчетов – поиск потенциала каждого узла (так называемый узловой потенциал). Существуют программы, позволяющие произвести онлайн расчет параметров по рассмотренным методам.

Базовые принципы

Произвольная электрическая цепь — это набор так называемых ветвей (рёбер), в которых находятся пассивные (резисторы, конденсаторы, индуктивности) и/или активные элементы. Пересечение (соединение) трёх и более ветвей называется узлом. Несколько ветвей могут образовывать замкнутые контуры. Для вычисления величин токов в ветвях применяют законы (или правила) Кирхгофа. Статус «правила» в данном случае корректнее, так как формулы Кирхгофа являются следствием закона сохранения заряда и фундаментальной теории Максвелла.

Рис.1 Графическое представление основных терминов МКТ

Прямолинейный, лобовой, подход подразумевает написание и решение системы уравнений «по максимуму». Пускай число узлов и ветвей равно Nу и Nр соответственно. Тогда потребуется составить следующее число уравнений:

• Nу -1 для токов (по первому правилу Кирхгофа);
• Nр – Nу +1 для напряжений по второму правилу Кирхгофа (ВПК).

Понятно, что чем больше уравнений в системе, тем сложнее и дольше будет длиться процесс её решения. Для облегчения расчетов были предложены алгоритмы, позволяющие существенно уменьшить число уравнений. МКТ является одной из таких методик, использующей (Nр – Nу + 1) уравнений по ВПК, дополненных понятием контурного тока — вспомогательной, гипотетической величиной.

Основные принципы

Любая электротехническая цепь состоит из участков (ветвей), образующих узлы и контуры. Для определения значений тока через любой элемент используют два закона Кирхгофа. Прямое составление уравнений дает систему с их максимальным количеством, равным количеству ветвей. В результате, если множество узлов цепи равно У, а число ветвей Р, то уравнения распределяются следующим образом:

• Для узлов У-1 по закону Кирхгофа для токов;
• Для ветвей Р-У+1 по закону Кирхгофа для напряжений.

Данное количество избыточно и приводит к образованию громоздкой системы уравнений большой размерности.

Для упрощения расчетов разработаны методики, которые позволяют сократить количество уравнений до приемлемых значений без снижения точности результатов. Наиболее простым является метод контурных токов.

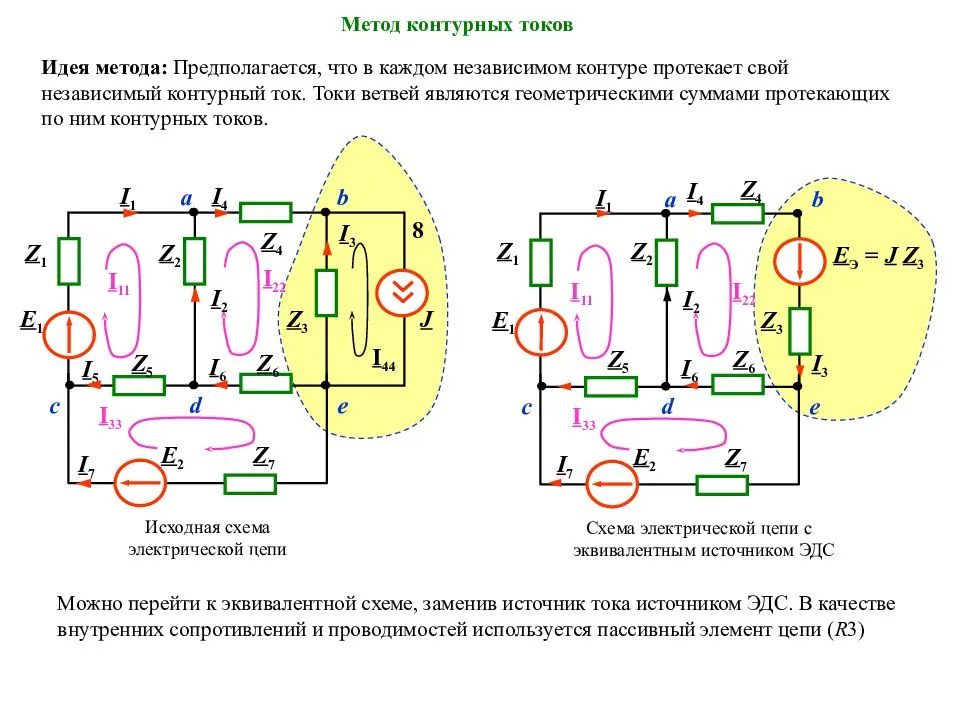
Анализ электрических цепей методом контурных токов

Ток в любой ветви можно представить составленным из нескольких токов, каждый из которых замыкается по своему контуру, оставаясь вдоль него неизменным. Такие составляющие называются контурными токами.

Эти токи (токи ветвей связи) принимаются в качестве независимых переменных. т.е. при анализе рассматриваются главные контуры:

На основании закона Ома

Умножая левую и правую части уравнения на матрицу B, получим:

В то же время I(В)= BTI(K);

Обозначая ℤ(K)= Bℤ(В)BT – матрица контурных сопротивлений, E(K)= BE(В)− Bℤ(В)J(В) – матрица контурных ЭДС, получим уравнение контурных токов в матричной форме:

Развёрнутая форма контурных уравнений:

Направление обхода контуров совпадает с направлением контурных токов (токов ветвей связи).

Пример.

Ветви связи – 2 и 3, n = 2, m = 3.

Матрица контуров:

Матрица сопротивлений:

Матрица контурных сопротивлений:

Предыдущая
РазноеЭлектролизсолей, щелочей, кислот
Следующая
РазноеСхемы подключения трехфазного счетчика. Установка трёхфазного счетчика

Построение системы уравнений

Резонанс в электрической цепи

Построение системы уравнений по рассматриваемой методике выполняется по следующим правилам:

• Для каждого выбранного контура задается направление обхода;
• С левой стороны равенств записывается сумма всех произведений искомых токов в ветвях на сопротивление веток. В правую часть записывается сумма источников напряжений, присутствующих в контуре;
• Если направление искомой величины или источника напряжения такое же, как у заданного направления обхода, то слагаемые пишутся со знаком «плюс», в ином случае они имеют отрицательное значение;
• Значение токов в ветвях заменяют на их выражение через токи контура.

После выполнения арифметических действий (раскрытие скобок, приведение подобных слагаемых) получается система уравнений, в которых неизвестными величинами являются виртуальные контурные токи.

Решая систему уравнений, получают значения контурных, а затем искомых величин.

3.2 Второй закон Кирхгофа

Второй закон Кирхгофа применяется к контурам и
формулируется следующим образом: алгебраическая сумма падений напряжений по
любому замкнутому контуру цепи равна алгебраической сумме ЭДС, действующих
вдоль этого же контура. Если в контуре нет ЭДС, то суммарное падение напряжений
равно нулю.

Для постоянных напряжений:

Для переменных напряжений:

Иными словами, при обходе цепи по контуру, потенциал,
изменяясь, возвращается к исходному значению. Если цепь содержит m ветвей, из
которых содержат источники тока ветви в количестве m_i, то она
описывается m-m_i– (у – 1) уравнениями напряжений.
Частным случаем второго правила для цепи, состоящей из одного контура, является
закон Ома для этой цепи.

Рисунок 2 – Схема электрическая принципиальная расчетной цепи

В итоге на схеме, рисунок 2, остаётся четыре узла, так как узел есть
точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения
двух линий на электрической схеме поставлена точка, то в этом месте есть
электрическое соединение двух линий, в противном случае его нет. Узел, в
котором сходятся две ветви, одна из которых является продолжением другой,
называют устранимым или вырожденным узлом.

Рассчитываю количество уравнений по первому и второму закону Кирхгофа.

у = 5 – число узлов;

в = 6 – число ветвей;

в_ит = 0 – число ветвей с источником тока.

Количество уравнений по первому закону Кирхгофа n1 = у −1 = 4 Количество уравнений по второму
закону Кирхгофа n2 = в − в_ит −(у − 1) = 4

Согласно первому заданию составляю системы уравнений по первому и второму
законам Кирхгофа. По 1-му закону Кирхгофа для (у-1) узлов схемы, с учетом токов
от источников тока, где y –
число узлов схемы. Уравнение для последнего узла не составляют, т.к. оно
совпало бы с уравнением, полученным при суммировании уже составленных уравнений
для предыдущих узлов (т.е. линейно-независимых уравнений – (y-1)). При составлении уравнений
следуют правилу: если ток выходит из узла, то его записывают со знаком
“-“, если входит – то со знаком “+”.

Уравнения по первому закону Кирхгофа:

1)       I_{1 +} I₂– I₃ = 0 (по 1 точке)

)         -I₁ – I₄ + I₅ = 0
(по 2 точке)

)         I₃ – I₄ – I₆ = 0 (по 3 точке)

) -I₂ – I₅ – I₆ = 0 (по 4 точке)

Для составления уравнений по второму закону Кирхгофа, используется
нарисованная схема, показанная на рисунке 3.

Рисунок 3 – Схема электрическая принципиальная расчетной цепи

Уравнения по второму закону Кирхгофа:

I.        I₁R₁ + I₂R₂
+ I₃R₃ = E₃ + E₂+ E₁

II.      -I₁R₁ – I₄R₄
+ I₅R₅ = E₁.  I₃R₃ + I₄R₄
+ I₆R₆ = E₃

IV.     -I₂R₂ – I₅R₅
– I₆R₆ = E₂

4. Метод контурных токов

Метод основан на введении промежуточной неизвестной величины – контурного
тока и использовании 2 закона Кирхгофа.

Контурный ток – собственный ток каждого независимого контура.

Реальный ток в ветвях определяется как алгебраическая сумма
соответствующих контурных токов. Число неизвестных в этом методе равно числу
уравнений, которые необходимо было бы составить для схемы по второму закону
Кирхгофа, то есть числу независимых контуров [(m – m_i) – (у – 1)].

Для каждого независимого контура (ячейки) составляют расчетное контурное
уравнение согласно правилу: левая часть равна сумме произведений контурного
тока на собственное сопротивление этого контура, взятое со знаком плюс, и
контурных токов прилегающих контуров на сопротивления смежных ветвей, взятых со
знаком минус: правая часть равна алгебраической сумме ЭДС этого контура –
контурной ЭДС.

Пусть электрическая цепь содержит n контуров (независимых). Согласно II
закону Кирхгофа получаем следующую систему из n линейных уравнений:

При этом следует считать , если условные положительные направления контурных токов в
одной ветви контуров K и m совпадают, и , если они противоположны.

где D1 D2 Dn – дополнение

D – определитель системы.

Расчёт установившегося режима в цепи переменного тока комплексным методом
выполняется в следующей последовательности:

Составляется электрическая схема, на которой все источники и пассивные
элементы представляются комплексными величинами соответственно напряжений,
токов, сопротивлений (проводимостей). Выбирается условно положительное
направление для комплексных значений напряжений, ЭДС и токов. Согласно
уравнениям электрических цепей (Ома, Кирхгофа) в комплексной форме составляются
алгебраические уравнения для рассчитываемой цепи. Уравнения цепи разрешаются
относительно искомых переменных (токов, напряжений) в их комплексной форме.

Метки

• алгоритм расчет цепей при несинусоидальных периодических воздействиях
• алгоритм расчета цепей периодического несинусоидального тока
• баланс мощностей
• ВАХ нелинейного элемента
• Векторная диаграмма
• ветви связи
• взаимная индуктивность
• взаимная проводимость
• вольт-амперная характеристика нелинейного элемента
• второй закон Кирхгофа
• второй закон Кирхгофа для магнитных цепей
• входная проводимость
• гармоники напряжения
• гармоники тока
• Генератор напряжения
• генератор тока
• главные контуры
• графический метод расчета нелинейных электрических цепей
• динамическое сопротивление
• дифференциальное сопротивление
• емкость двухпроводной линии
• емкость коаксиального кабеля
• емкость конденсатора
• емкость однопроводной линии
• емкость плоского конденсатора
• емкость цилиндрического конденсатора
• закон Ампера
• закон Био Савара Лапласа
• закон Ома
• закон полного тока
• закон электромагнитной индукции
• Законы Кирхгофа
• индуктивность
• индуктивность двухпроводной линии
• индуктивность однопроводной линии
• индуктивность соленоида
• катушка со сталью
• Конденсатор в цепи постоянного тока
• контурные токи
• коэффициент амплитуды
• коэффициент гармоник
• коэффициент искажения
• коэффициент магнитной связи
• коэффициент мощности трансформатора
• коэффициент трансформации
• коэффициент формы
• кусочно-линейная аппроксимация
• магнитная постоянная
• магнитная цепь
• магнитный поток рассеяния
• метод активного двухполюсника
• метод двух узлов
• метод контурных токов
• метод наложения
• метод узловых напряжений
• метод узловых потенциалов
• метод эквивалентного генератора
• метод эквивалентного источника ЭДС
• Метод эквивалентных преобразований
• методы расчета магнитных цепей
• независимые контуры
• нелинейный элемент
• несинусоидальный периодический ток
• обобщенный закон Ома
• опорный узел
• основной магнитный поток
• параллельное соединение конденсаторов
• первый закон Кирхгофа
• первый закон Кирхгофа для магнитных цепей
• последовательное соединение конденсаторов
• последовательный колебательный контур
• постоянная составляющая тока
• потери в меди
• потери в стали
• приведенный трансформатор
• Примеры расчета схем при несинусоидальных периодических воздействиях
• принцип взаимности
• принцип компенсации
• расчет гармоник тока
• расчет магнитной цепи
• расчет нелинейных цепей постоянного тока
• расчет цепей несинусоидального тока
• Расчет цепи конденсаторов
• расчет цепи с несинусоидальными периодическими источниками
• Резонанс в электрической цепи
• решение задач магнитные цепи
• сила Ампера
• сила Лоренца
• Символический метод
• собственная проводимость
• статическое сопротивление
• сферический конденсатор
• теорема об эквивалентном источнике
• теорема Тевенена
• топографическая диаграмма
• Трансформаторы
• трехфазная система
• удельная энергия магнитного поля
• уравнения трансформатора
• Цепи с конденсаторами
• частичные токи
• чередование фаз
• ЭДС самоиндукции
• эквивалентная схема трансформатора
• электрическая постоянная
• электроемкость
• энергия магнитного поля

Классификация электрических цепей

По назначению электрические цепи бывают:

• Силовые электрические цепи;
• Электрические цепи управления;
• Электрические цепи измерения;

Силовые цепи предназначены для передачи и распределения электрической энергии. Именно силовые цепи ведут ток к потребителю.

Также цепи разделяют по силе тока в них. Например, если ток в цепи превышает 5 ампер, то цепь силовая. Когда вы щелкаете чайник, включенный в розетку, Вы замыкаете силовую электрическую цепь.

Электрические цепи управления не являются силовыми и предназначены для приведения в действие или изменения параметров работы электрических устройств и оборудования. Пример цепи управления – аппаратура контроля, управления и сигнализации.

Электрические цепи измерения предназначены для фиксации изменений параметров работы электрического оборудования.

Определение и суть метода контурных токов

Векторная диаграмма токов и напряжений

По данному методу в исследуемой цепи выделяются независимые плоские замкнутые контуры, включающие все, без исключения, элементы. Предполагается, что в каждом контуре может протекать некоторый контурный ток. В том случае, если цепь с элементом принадлежит только одному контуру, то ток через входящие в нее элементы равен контурному. Если элемент охватывается несколькими контурами, то он в ней равен алгебраической (с учетом направления) сумме контурных токов.

Важно! Суммирование должно производиться строго с учетом направления движения при обходе контура. Знак «плюс» – при совпадении направления, «минус» – при противоположном

При составлении уравнений учитываются входящие в схему источники ЭДС и тока.

На пpaктике удобнее преобразовать идеальный источник тока в идеальный источник ЭДС. Преобразование выполняется согласно закона Ома:

U=I∙r, где r – внутреннее сопротивление источника тока (напряжения).

Методика расчета используется как в цепях постоянного, так и переменного напряжения. При расчетах цепей переменного напряжения с реактивными элементами используются комплексные величины, затем вычисляются мгновенные и амплитудные величины токов и напряжений и углы сдвига фаз между ними.

Основные принципы

Любая электротехническая цепь состоит из участков (ветвей), образующих узлы и контуры. Для определения значений тока через любой элемент используют два закона Кирхгофа. Прямое составление уравнений дает систему с их максимальным количеством, равным количеству ветвей. В результате, если множество узлов цепи равно У, а число ветвей Р, то уравнения распределяются следующим образом:

• Для узлов У-1 по закону Кирхгофа для токов;
• Для ветвей Р-У+1 по закону Кирхгофа для напряжений.

Данное количество избыточно и приводит к образованию громоздкой системы уравнений большой размерности.

Для упрощения расчетов разработаны методики, которые позволяют сократить количество уравнений до приемлемых значений без снижения точности результатов. Наиболее простым является метод контурных токов.

Пример реальной цепи

Самую простую электрическую цепь можно сделать самостоятельно. Её часто собирают на уроке физики. При этом не стоит опасаться поражения током, так как в ней будет использоваться низковольтный источник напряжения. Но всё же перед тем как приступить к сборке, следует знать о коротком замыкании. Под ним понимают состояние, при котором происходит закорачивание выхода.

Другими словами, вся энергия источника тока оказывается приложенной к нему же. В результате разность потенциалов снижается до нуля, а в цепи возникает максимальная сила тока. Непреднамеренное короткое замыкание может привести к выходу из строя генератор и радиодетали. Именно для защиты от этого пагубного воздействия в цепи ставят предохранитель.

Схема для самостоятельного повторения будет представлять собой узел управления освещением. Для её сборки необходимо подготовить:

Источник питания на 12 вольт. Это может быть аккумулятор, регулируемый лабораторный блок, батарейки. Главное, чтобы источник смог выдавать нужное напряжение. Например, нужную величину можно получить соединив последовательно несколько батареек со стандартным номиналом 1,5 В (1,5 * 4 = 12 В).
Лампочка

Подойдёт накаливания
Здесь важно обратить внимание на её характеристики. Она должна быть рассчитанной на нужное напряжение.
Ключ
Это обыкновенный выключатель, имеющий два устойчивых состояния — разомкнутое и замкнутое.
Провода

В сборке можно использовать любые медные проводники сечением от 0,25 мм 2 .

Электрическая цепь включает (в общем случае): источник питания, рубильник (выключатель), соединительные провода, потребителей. Обязательно сформируйте замкнутый контур. В противном случае по цепи не сможет течь ток. Электрическими не принято называть контуры заземления, зануления. Однако по сути считаются таковыми, иногда здесь течет ток. Замыкание контура при заземлении, занулении обеспечивается посредством грунта.

Источники питания. Внутренняя, внешняя электрическая цепь

Для образования упорядоченного движения носителей заряда, формирующего ток, потрудитесь создать разность потенциалов на концах участка. Достигается подключением источника питания, который в физике принято называть внутренней электрической цепью. В противовес прочим элементам, составляющим внешнюю. В источнике питания заряды движутся против направления поля. Достигается приложением сторонних сил:

1. Обмотка генератора.
2. Гальванический источник питания (батарейка).
3. Выход трансформатора.

Напряжение, формируемое на концах участка электрической цепи, бывает переменным, постоянным. Сообразно в технике принято контуры делить соответствующим образом. Электрическая цепь предназначена для протекания постоянного, переменного тока. Упрощенное понимание, закон изменения упорядоченного движения носителей заряда воспринимается сложным. С трудом понимаем, переменный в цепи ток или постоянный.

Род тока определен источником, характером внешней электрической цепи. Гальванический элемент дает постоянное напряжение, обмотки (трансформаторы, генераторы) – переменное. Связано с протекающими в источнике питания процессами.

Сторонние силы, обеспечивающие движения зарядов, называют электродвижущими. Численно ЭДС характеризуется работой, совершаемой генератором для перемещения единичного заряда. Измеряется вольтами. На практике для расчета цепей удобно делить источники питания двумя классами:

1. Источники напряжения (ЭДС).
2. Источники тока.

В действительности неизвестны, имитацию пытаются создать практики. В розетке ожидаем увидеть 230 вольт (220 вольт по старым нормативам). Причем ГОСТ 13109 однозначно устанавливает пределы отклонения параметров от нормы. В быту пользуемся источником напряжения. Параметр нормируется. Величина тока не играет значения. Напряжение подстанции круглые сутки стремятся сделать постоянным вне зависимости от текущего запроса потребителей.

В противовес источник тока поддерживает заданный закон упорядоченного движения носителей заряда. Значение напряжения роли не играет. Ярким примером подобного рода устройств выступает сварочный аппарат на базе инвертора. Каждый знает: диаметр электрода прочно связан с толщиной металла, прочими факторами. Чтобы процесс сварки шел правильно, приходится с высокой степенью постоянства поддерживать ток. Задачу решает электронный блок на основе инвертора.

Ток, напряжение бывают постоянными, переменными. Закон изменения параметра роли не играет

Неважно, подключать ли электрическую цепь к источнику постоянного, переменного напряжения. Однако важно выдержать правильный размер параметра

К примеру, действующее значение ЭДС.