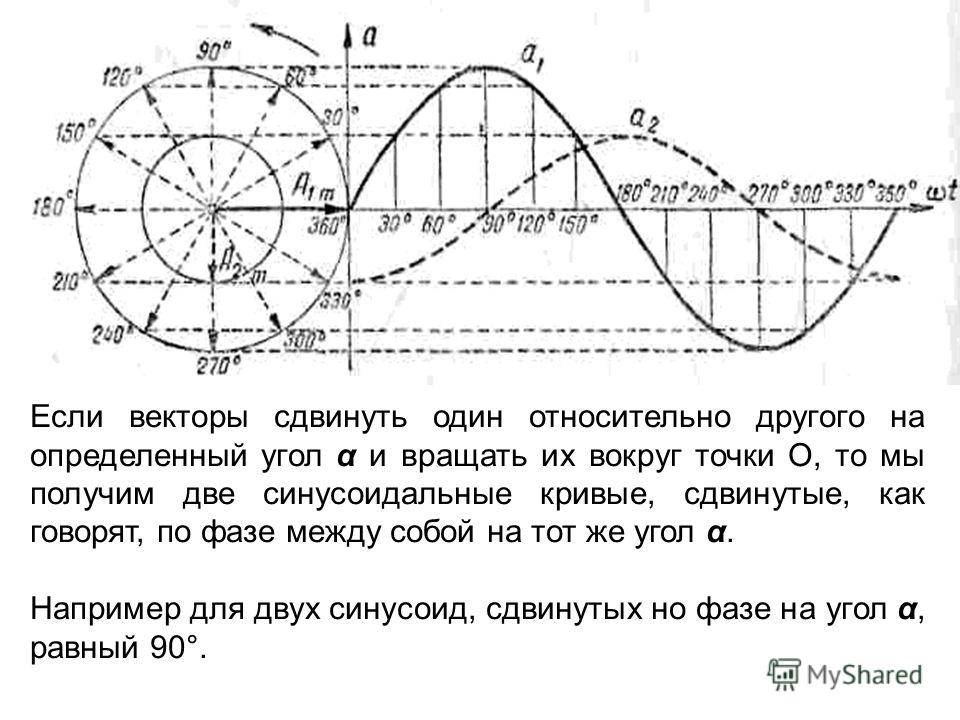
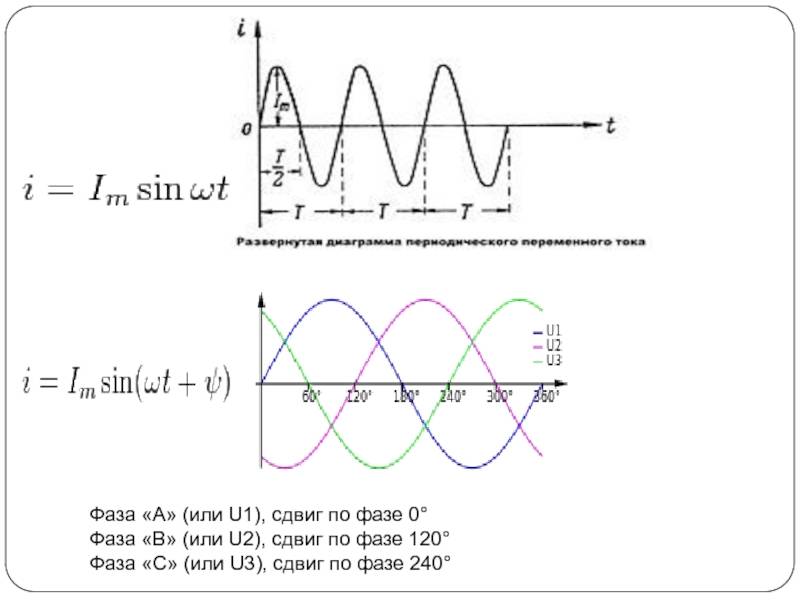
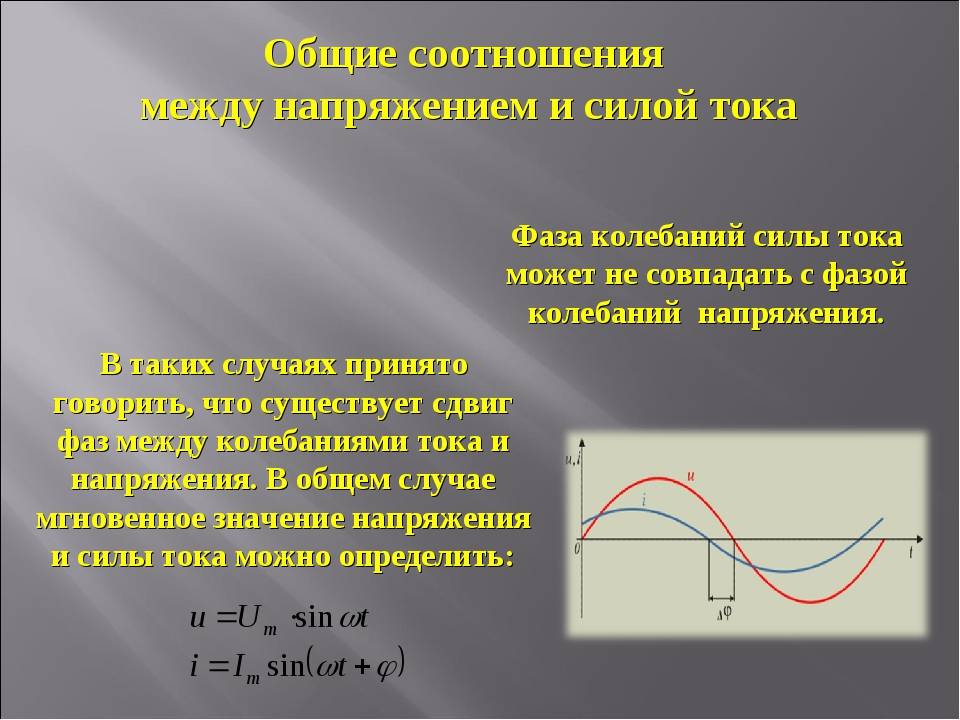
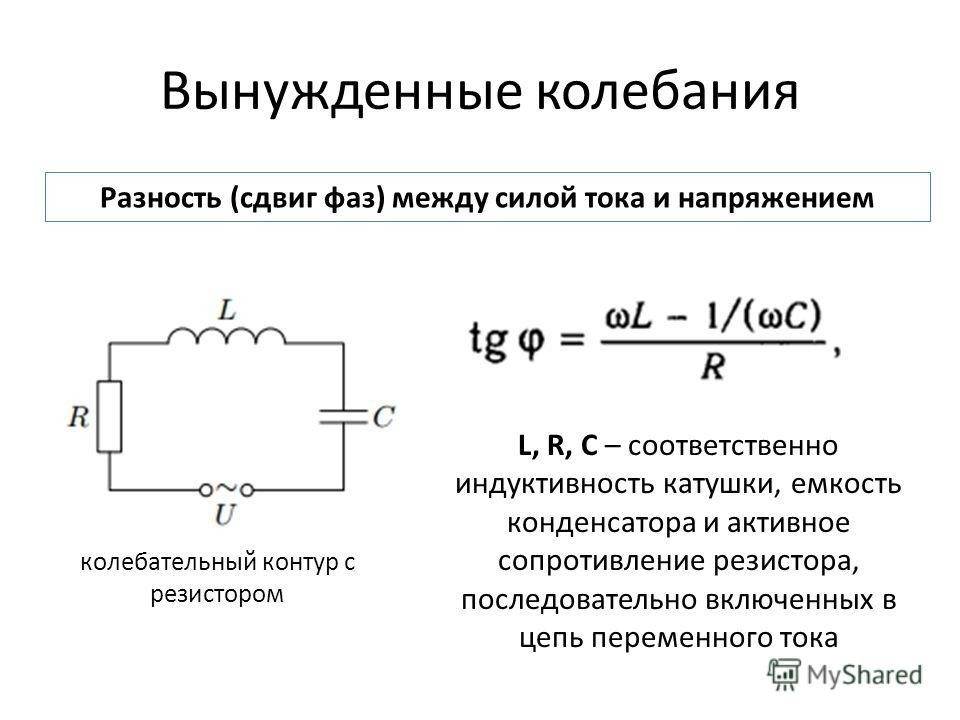
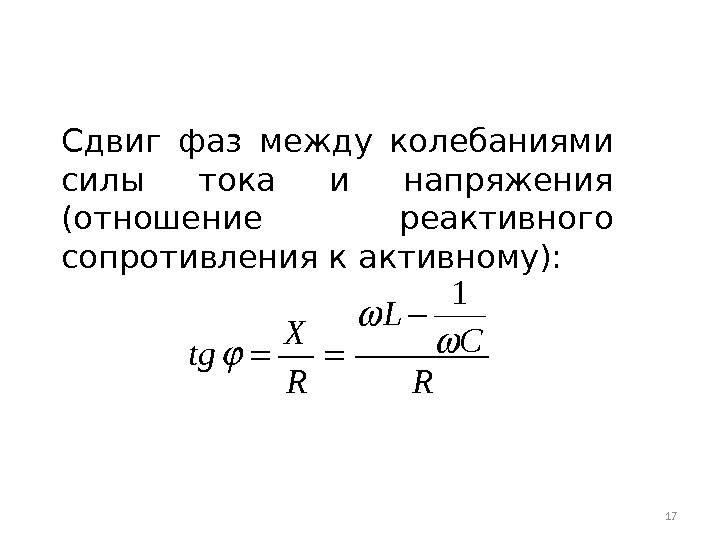Определение и общие сведения о деформации сдвига
Основным признаком, характеризующим деформацию сдвига, является сохранение постоянства объёма. Не зависимо от того, в каком направлении действуют силовые факторы этот параметр остаётся неизменным.
Примеры проявления деформации сдвига можно обнаружить при проведении различного рода работ. К таким случаям относятся:
- при распиловке бруса;
- отрезание или рубка металла;
- в результате нарушения целостности крепления металлических или деревянных деталей, соединённых метизами;
- балки в местах крепления опор;
- места скрепления мостовых пролётов;
- крепёж на перемычках соединения железнодорожных рельс;
- разрезания листа бумаги ножницами.
При определённых условиях наблюдается чистый сдвиг. Он определяется как сдвиг, при котором на все четыре грани (например, прямоугольной детали) оказывают воздействие только напряжения, направленные по касательной к поверхности. В этом случае произойдёт плавный сдвиг всех слоёв детали от верхних к нижним слоям. Тогда внешняя сила изменяет форму детали, а объём сохраняется.
Для оценки величины сдвига и надёжности конструкции используют следующие параметры:
- величина, направление и точка приложения воздействующей силы;
- модуль сдвига;
- угол изменения внешних граней изделия;
- тангенциальное напряжение;
- модуль кручения (зависит от физико-механических характеристик материала);
Расчёт и практическое измерение этих параметров необходимы для оценки устойчивости и целостности конструкции. Формула, позволяющая вычислить допустимые изменения, учитывает все воздействия на конкретные слои детали и всю конструкции в целом.
В случае воздействия деформации величина угла считается пропорциональной внешней силе. Увеличение степени воздействия может превратить деформацию сдвига в срез. Это приведёт к разрушению не только элементов крепления (болтов, шпилек, заклёпок), но и всей детали.
Для наглядности изменения формы детали при деформации сдвига динамика процесса обозначается с помощью величины угла смещения и векторов возникающих напряжений. Действующая сила направлена в сторону смещения слоёв рассматриваемой детали.

В современных условиях угол сдвига измеряется различными техническими приборами. Основным прибором для измерения параметров смещения является тензомер. Эти приборы работают на различных физических принципах:
- оптические (в том числе лазерные);
- акустические;
- рентгеновские; электрические;
- пневматические.
В этих приборах относительная деформация сдвига обрабатывается на современных вычислительных средствах с применением соответствующего программного обеспечения. Каждый метод обладает своими достоинствами и недостатками. Их применение зависит от поставленной задачи, технической и финансовой возможности.
Что такое переменное напряжение?
Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени.
Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени. Данная статья посвящена периодическому переменному напряжению.

Постоянное (слева), периодическое (в центре) и непериодическое (справа) переменное напряжение.
Минимальное время, за которое значение переменного напряжения повторяется, называется периодом. Любое периодическое переменное напряжение можно описать какой-либо функциональной зависимостью. Если время обозначить через t, то такая зависимость будет иметь вид F(t), тогда в любой период времени зависимость будет иметь вид
где Т – период.
Величина обратная периоду Т, называется частотой f. Единицей измерения частоты является Герц, а единицей измерения периода является Секунда
Наиболее часто встречающаяся функциональная зависимость периодического переменного напряжения является синусоидальная зависимость, график которой представлен ниже

Синусоидальное переменное напряжение.
Из математики известно, что синусоида является простейшей периодической функцией, и все другие периодические функции, возможно, представить в виде некоторого количества таких синусоид, имеющих кратные частоты. Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.
Таким образом, синусоидальное напряжение в любой момент времени, мгновенное напряжение, описывается следующим выражением
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла),
φ – начальная фаза, определяемая смещением синусоиды относительно начала координат, определяется точкой перехода отрицательной полуволны в положительную полуволну.
Величина (ωt + φ) называется фазой, характеризующая значение напряжения в данный момент времени.
Таким образом, амплитуда Um, угловая частота ω и начальная фаза φ являются основными параметрами переменного напряжения и определяют его значение в каждый момент времени.
Обычно, при рассмотрении синусоидального напряжения считают, что начальная фаза равна нулю, тогда
В практической деятельности, довольно часто, используют ещё ряд параметров переменного напряжения, такие как, действующее напряжение, среднее напряжение и коэффициент формы, которые мы рассмотрим ниже.
Особенности трехфазных систем электропитания
Итак, ключевым недостатком однофазных систем переменного напряжения является неравномерность генерации и транспортировки энергии (Рисунок 5). И этой особенности лишены трехфазные системы, которые сейчас используются во всем мире.
Трехфазную систему электроснабжения можно упрощенно представить в виде трех одинаковых систем, напряжения в которых сдвинуты по фазе на треть периода – 120 градусов или 2π/3 радиан. Получить трехфазное напряжение можно, например, с помощью трех отдельных однофазных генераторов переменного напряжения, роторы которых расположены на одном валу, но повернуты на 120°. Однако наилучший эффект будет в случае, когда все три обмотки будут расположены на общем магнитопроводе статора генератора (Рисунок 10). В таком устройстве при равномерном вращении ротора с постоянным магнитом в каждой обмотке будет генерироваться переменное синусоидальное напряжение, сдвинутое по фазе на 120° по отношению к напряжению других обмоток.
 | |
| Рисунок 10. | Принцип работы трехфазного генератора. |
В простейшем случае каждую обмотку можно подключить к своему потребителю и получить три изолированные и практически независимые системы электропитания. Однако в этом случае теряются все преимущества трехфазного напряжения, поэтому все три обмотки соединяют вместе. Различают два способа соединения: «треугольником», когда начало одной обмотки соединяется с концом другой, и «звездой», когда начала обмоток соединяются вместе, а соединительные провода подключаются к концам обмоток (Рисунок 11). Достоинства и недостатки каждого из способов соединения взаимно компенсируют друг друга, поэтому энергетики, за исключением «последней мили», одинаково часто используют оба способа. Более того, трехфазная система позволяет смешивать оба типа соединений, например, обмотки генератора могут быть соединены по схеме «треугольник», а потребители – по схеме «звезда».
 | |
| Рисунок 11. | Схемы соединения в трехфазной сети. |
Ключевыми преимуществами трехфазной системы являются наименьшая стоимость линий электропередач, поскольку для передачи энергии необходимы три провода с меньшим суммарным сечением, чем при использовании двух проводов, а также равномерная скорость передачи энергии. Несмотря на то, что мощность в каждой обмотке генератора пульсирует с удвоенной частотой напряжения, общая мощность всех трех обмоток в любой момент времени постоянна (при условии, что все обмотки имеют одинаковые нагрузки). Это обстоятельство значительно упрощает конструкцию генераторов и электродвигателей – основных потребителей электрической энергии в промышленности. Кроме этого, трехфазное оборудование оказывается меньше, легче, чем однофазное той же мощности []. Например, трехфазные трансформаторы за счет использования общего для всех трех фаз магнитопровода оказываются меньше, легче и дешевле трех однофазных трансформаторов такой же суммарной мощности.
Теперь становится понятно, почему во всем мире трехфазные системы электропитания имеют наибольшую популярность – передавать энергию с меньшими затратами человек пока еще не научился. Однако все, что было рассмотрено выше, интересует больше энергетиков – это их область. Специалистов в области электроники и информационных технологий, а также простых пользователей бытовых электроприборов больше интересует «последняя миля» глобальной энергосистемы – домашняя и офисная электропроводка, ведь именно с ней связано бóльшая часть реальных проблем, которые приходится решать самостоятельно. Поэтому давайте разбираться дальше.
Угол сдвига фаз между током и напряжением
Начальные фазы электромагнитных синусоидальных колебаний первичного и вторичного напряжения, с частотой одинаковой величины, могут существенно различаться на некоторый угол сдвига фаз (угол φ). Переменные величины могут неоднократно в течение определенного периода некоторого времени изменяются с определенной частотой. Если электрические процессы имеют неизменный характер, а сдвиг фаз равен нулю, это свидетельствует о синхронизме источников величин переменного напряжения, например, трансформаторов. Сдвиг фазы служит определяющим фактором коэффициента мощности в электрических сетях переменного тока.
Угол сдвига фаз находится при необходимости, тогда, если один из сигналов является опорным, а второй сигнал с фазой в самом начале совпадает с углом сдвига фаз.
Измерение угла сдвига фаз производится прибором, в котором присутствует нормированная погрешность.
Фазометр может производить измерение угла сдвига в границах от 0 о до 360 о в некоторых случаях от -180 о С до +180 о С, а диапазон измеряемых частот сигналов может колебаться от 20Гц до 20 ГГц. Измерение гарантируется в том случае если напряжение входного сигнала равно от 1 мВ до 100 В, если же напряжение входного сигнала превышает эти границы точность измерения не гарантируется.
Пролог
Музыканты, меломаны, а так же, любители “хай-эндовского” звука, в разговорах между собой, часто используют, вроде бы всем понятные термины – спектр, фаза, частота, меандр, глубина и локализация сцены, и прочие узкозначимые слова. Но зачастую, даже некоторые из “знатоков”, до конца не могут понять, что же это на самом деле такое.
Такие понятия как – “Фазовый сдвиг” очень часто упоминаются при проектировании кроссоверов для акустики. Подробно про кроссоверы мы уже поговорили чуть ранее.
При наличии интернета выяснить тот или иной вопрос не составляет проблем. В отсутствии такового – можно сходить в библиотеку, найти пару реально научных книжек и почитать саму теорию. Но все нынче стали на столько занятые, что даже выуживать информацию из интернета – времени нет. Попробуем найти простое объяснение – что же такое “фазовый сдвиг”?
Что означают эти термины на самом деле? Можно ли “пощупать” их истинное значение? Да, однозначно, можно. Сейчас мы попробуем разобраться в вопросе – “Что такое – фазовый сдвиг?”
Явление резонанса. Резонанс напряжений
Свойства цепи при резонансе напряжения.
На рисунке 3 приведена векторная диаграмма для цепи
в случае, когда
1.Полное сопротивление последовательного контура при резонансе напряжений минимально и равно активному сопротивлению.
Из выражения:
-полное сопротивление когда цепь не настроена в резонанс.
Следует что при резонансе когда
, или
2. Ток в контуре при резонансе напряжений максимален и ввиду чисто активного сопротивления контура совпадает по фазе с приложенным напряжением.
; при ,
3. Напряжение генератора переменного тока, включенного в цепь расходуется на активном сопротивлении:
4.Напряжение на индуктивности и емкости определяется по закону Ома.
5. В последовательно соединенных сопротивлениях протекает одинаковый ток, при резонансе
, и напряжения будут равны: или
6. Если одновременно увеличить оба реактивных сопротивления
. То возрастут оба частичных напряжения , а сила тока в цепи не изменится. Таким путём можно получить во много раз больше, чем напряжение цепи.
7. На векторной диаграмме видно, что напряжение на индуктивности и напряжение на ёмкости равны и сдвинуты по фазе друг относительно друга на 180 градусов и взаимно компенсируются (рисунок 3).
Угол сдвига фаз между током и напряжением при резонансе равен нулю.
Это значит, что ток и напряжение совпадают по фазе (как в цепи с активным сопротивлением). Поэтому величина тока ограничивается только небольшим сопротивлением.
Вывод: Цепь носит активный характер, энергия полей в источник не поступает. Настройку контура в резонанс можно производить как изменением частоты источника, так и изменением частоты колебаний контура, а также изменением либо индуктивности, либо ёмкости контура.
Особенности домашней и офисной электропроводки
«Последняя миля» системы электроснабжения начинается после последней трансформаторной подстанции, понижающей напряжение до величины 0.4 кВ. Первичные обмотки последнего понижающего трехфазного трансформатора могут быть соединены по любой схеме («треугольник» или «звезда» – как удобно энергетикам), но вторичные обычно всегда подключают по схеме «звезда». Причем точку соединения обмоток трансформатора электрически соединяют с землей, и к этой точке идет дополнительный провод, называемый «нулевым». Таким образом, электрическая энергия от понижающей трансформаторной подстанции поступает к потребителям по четырем проводам, из которых три являются «фазными» (фаза А, фаза В и фаза С), а четвертый – нулевым (Рисунок 12).
| Рисунок 12. | Напряжения в трехфазной сети. |
Напряжение каждой из вторичных обмоток трансформатора равно 230 В. Таким образом, напряжение между нулевым и любым из фазных проводов равно 230 В. Это напряжение энергетики называют «фазным». Но если измерить напряжение между любыми двумя фазными проводниками, то окажется, что оно будет приблизительно равно 400 В, что почти в два раза больше. Это напряжение называют «линейным». Точное соответствие между фазными VF и линейными VL напряжениями определяется формулой:
| (11) |
Происходит это из-за того, что фазные напряжения сдвинуты по фазе на 120°, из-за чего и происходит это увеличение (Рисунок 13). При этом результирующее напряжение является синусоидальным, но сдвинутым по фазе на –5π/6 (–150°) по отношению к опорной фазе (фазе, потенциал которой принят в качестве нулевого при проведении измерений).
| Рисунок 13. | Принцип формирования линейных напряжений. |
Возможность получения нескольких напряжений является еще одним преимуществом трехфазной системы, ведь, как известно из предыдущей статьи, чем выше напряжение питания, тем меньше ток в цепи и дешевле электрические кабели. Таким образом, маломощных потребителей, теоретически, можно подключать к фазному напряжению 230 В, а мощных – к линейному 400 В, что позволит по одному и тому же кабелю пропустить в 1.732 раза больше энергии.
Однако на практике поступают немного иначе. Маломощных потребителей, действительно, подключают к одной из фаз системы электроснабжения, а мощных – сразу к трем фазам (Рисунок 14). В этом случае мощные потребители потребляют энергию сразу из трех фаз, что обеспечивает равномерное распределение механической нагрузки на вал генератора электростанции и уменьшает потери при транспортировке электричества.
| Рисунок 14. | Способы подключения потребителей разной мощности. |
В системах электроснабжения «мощными» считаются потребители, имеющие мощность более 1 кВт. Начиная с этого уровня, трехжильные медные кабели становятся дешевле двужильных. Из-за этого очень сложно найти однофазное оборудование с мощностью более 2.5 кВт. По этой же причине максимальный ток большинства электрических розеток не превышает 16 A. При таком токе максимальная мощность, которую можно потребить от розетки, равна 230∙16 ≈ 3.7 кВт, что вполне достаточно для питания большинства однофазных приборов.
ФИЗИКА
§ 2.9. Закон Ома для электрической цепи переменного тока
Рассмотрим теперь более общий случай электрической цепи, в которой последовательно соединены проводник с активным сопротивлением R и малой индуктивностью, катушка с большой индуктивностью L и малым активным сопротивлением и конденсатор емкостью С (рис. 2.20).
Рис. 2.20
Чему равна амплитуда силы тока в такой цепи (колебательном контуре), если на ее концах поддерживается напряжение u(t) = U sin ωt?
Мы видели, что при включении по отдельности в цепь проводника с активным сопротивлением R, конденсатора емкостью С или катушки с индуктивностью L амплитуда силы тока определяется соответственно формулами (2.6.2), (2.7.3) и (2.8.4). Амплитуды же напряжений на резисторе, катушке индуктивности и конденсаторе связаны с амплитудой силы тока так:

В цепях постоянного тока напряжение на концах цепи равно сумме напряжений на отдельных последовательно соединенных участках цепи. Однако, если измерить результирующее напряжение на контуре и напряжения на отдельных элементах цепи переменного тока, окажется, что напряжение на контуре (действующее значение) не равно сумме напряжений на отдельных элементах.
Почему это так? Дело в том, что гармонические колебания напряжения на различных участках цепи сдвинуты по фазе друг относительно друга.
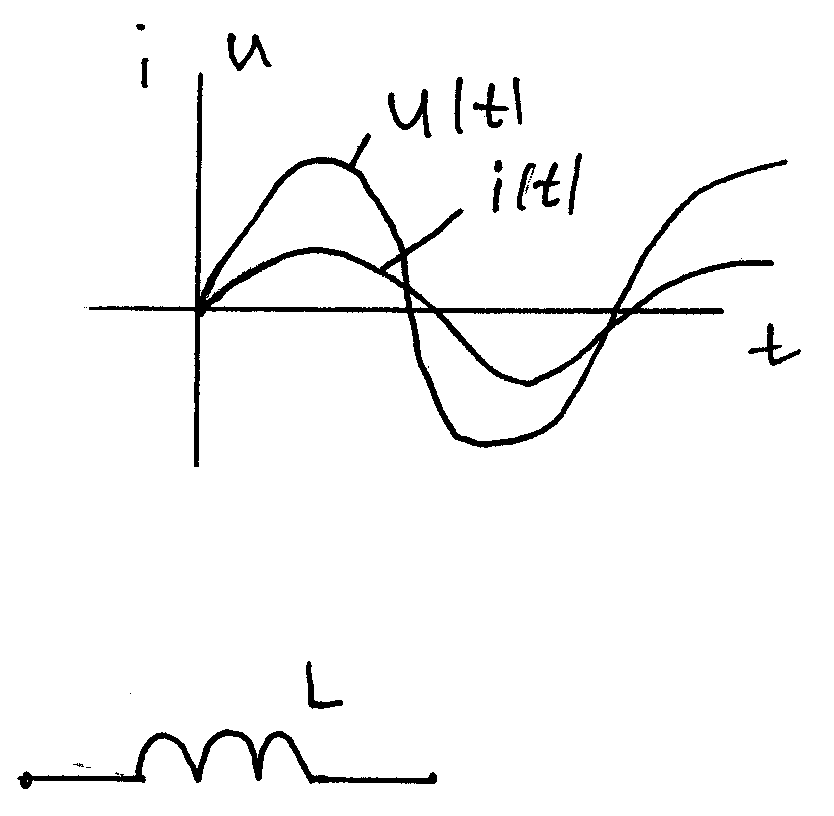
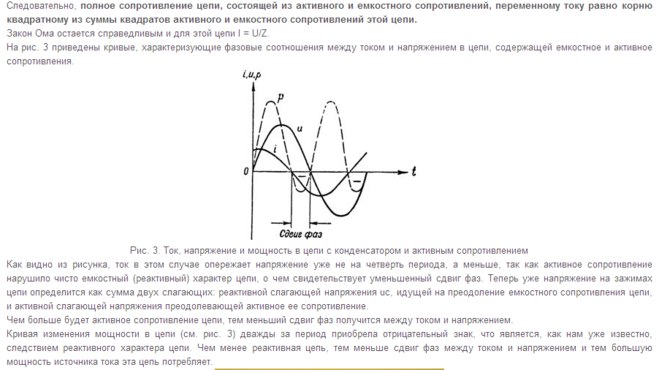
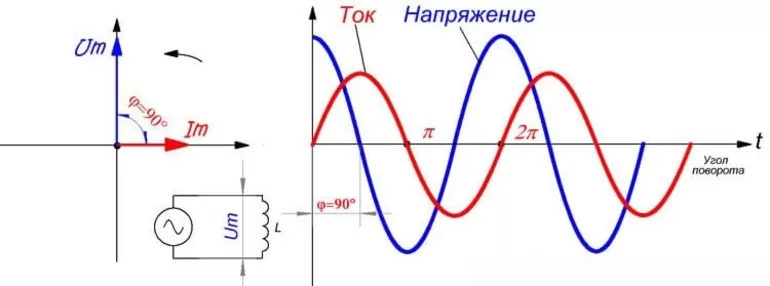
Действительно, квазистационарный ток в любой момент времени одинаков во всех участках цепи. Это значит, что одинаковы амплитуды и фазы токов, протекающих по участкам с емкостным, индуктивным и активным сопротивлением. Однако только на участке с активным сопротивлением колебания напряжения и силы тока совпадают по фазе. На конденсаторе колебания напряжения отстают по фазе от колебаний силы тока на π/2 (см. § 2.7), а на катушке индуктивности колебания напряжения опережают колебания силы тока на π/2 (см. § 2.8).
Векторная диаграмма электрической цепи
Для вывода закона Ома в случае электрической цепи переменного тока, изображенной на рисунке 2.20, нужно уметь складывать мгновенные колебания напряжений, сдвинутых по фазе друг относительно друга. Проще всего выполнять сложение нескольких гармонических колебаний с помощью векторных диаграмм, о которых было рассказано в § 1.11. Векторная диаграмма электрических колебаний в цепи позволит нам определить амплитуду силы тока в зависимости от амплитуды напряжения и сдвиг фаз между силой тока и напряжением.
Так как сила тока одинакова во всех участках цепи, то построение векторной диаграммы удобно начать с вектора силы тока m. Этот вектор изобразим в виде вертикальной стрелки (рис. 2.21). Напряжение на резисторе совпадает по фазе с силой тока. Поэтому вектор mR должен совпадать по направлению с вектором m. Его модуль равен UmR = ImR.
Рис. 2.21
Колебания напряжения на катушке индуктивности опережают колебания силы тока на π/2 и соответствующий вектор и mL должен быть повернут относительно вектора m на π/2. Его модуль равен UmL = IωL. Если считать, что положительному сдвигу фаз соответствует поворот вектора против часовой стрелки, то вектор mL следует повернуть налево на π/2. (Можно было бы, конечно, поступить и наоборот.)
Вектор напряжения на конденсаторе mC отстает по фазе от вектора m на π/2 и поэтому повернут на этот угол относительно вектора m направо. Его модуль равен .
Для нахождения вектора суммарного напряжения m нужно сложить три вектора: mR, mL и mC. Вначале удобнее сложить два вектора mL и mC (рис. 2.22).
Рис. 2.22
Модуль этой суммы равен , если . Именно такой случай изображен на рисунке. После этого, сложив вектор mL + mC с вектором mR, получим вектор m, характеризующий колебания напряжения в сети.
По теореме Пифагора (из треугольника АОВ):

или

Из равенства (2.9.2) можно найти амплитуду силы тока в цепи:

Это и есть закон Ома для электрической цепи переменного тока, изображенной на рисунке 2.20.
Благодаря сдвигу фаз между напряжениями на различных участках цепи полное сопротивление Z цепи (см. рис. 2.20) выражается так:

От амплитуд силы тока и напряжения можно перейти к действующим значениям этих величин. Они связаны друг с другом точно так же, как и амплитуды в формуле (2.9.3):

Мгновенное значение силы тока меняется со временем гармонически:

где φc, — разность фаз между силой тока и напряжением в сети. Она зависит от частоты со и параметров цепи R, L, С.
Сдвиг фаз между током и напряжением
Сдвиг фаз φc, между колебаниями силы тока и напряжения равен по модулю углу φ между векторами m и m (см. рис. 2.22). Как следует из этого рисунка,

Согласно рисунку 2.22, сила тока отстает от напряжения по фазе при условии . Поэтому сдвиг фаз φc = -φ и

В частных случаях цепей с активным, емкостным и индуктивным сопротивлениями из этой формулы получаются правильные значения сдвига фаз.
В чем отличие полярного и неполярного?
Неполярные допускают включение конденсаторов в цепь без учета направления тока. Элементы применяются в фильтрах переменных источников питания, усилителях высокой частоты.
Полярные изделия подсоединяют в соответствии с маркировкой. При включении в обратном направлении прибор выйдет из строя или не будет нормально работать.
Полярные и неполярные конденсаторы большой и малой ёмкости отличаются конструкцией диэлектрика. В электролитических конденсаторах, если оксид наносится на 1 электрод или 1 сторону бумаги, пленки, то элемент будет полярным.
Модели неполярных электролитических конденсаторов, в конструкциях которых оксид металла нанесли симметрично на обе поверхности диэлектрика, включают в цепи с переменным током.
У полярных на корпусе присутствует маркировка положительного или отрицательного электрода.
Метод векторных диаграмм
Мы уже пользуемся векторными диаграммами, по которым наблюдаем соотношения токов и напряжения в цепях переменного тока. Векторная диаграмма это стоячее изображение вращающихся векторов.
В предыдущих рассуждениях, было сказано, что линейно развернутая диаграмма переменного процесса, (в простом случае синусоидального), точно показывает изменение мгновенного значения переменной величины, то есть происходит все именно так как показывает синусоида и каждая ее точка и есть переменная величина в данный момент. Но оказывается нам интересно не это, нам нужно знать какое значение тока и напряжения и мощности действует в цепи в течение времени, то есть действует длительное время, пока цепь работает.
Анализ синусоид нескольких величин, одновременно действующих в разных фазах, позволяет рассчитать все свойства и режимы работы цепи переменного тока, но гораздо проще это сделать, если отвлечься от синусоид и просто построить соотношение векторов, которые, собственно, и образуют эти синусоиды. Вся информация синусоид заложена в их радиус – векторах. Мы останавливаем эти векторы на рисунке, понимая, что они вращающиеся, но факт их вращения учитываем угловой частотой в расчетных формулах векторной диаграммы.
Итак, векторная диаграмма заменяет линейно развернутую синусоидальную диаграмму, потому, что любая информация, заложенная в синусоиду, есть и в соответствующем ей радиус-векторе.
Если нам приходится рассматривать несколько действующих одновременно синусоидальных процессов, то они изображаются векторной диаграммой, где длина каждого вектора, соответствует действующему значению синусоидальной величины, направление вектора соответствует начальной фазе, синусоидальной величины.
Результирующие значения одновременно действующих напряжений рассчитывается как векторная сумма, где угол между векторами определяется сдвигом фаз между ними.
Расчет цепей переменного тока сводится к расчету треугольников, которые состоят из соответствующих векторов.
Например, можно определить суммарное напряжение, частичные напряжения, и сдвиг фаз между ними.
На основании векторных диаграмм можно построить подобные векторным диаграммам треугольники сопротивлений и треугольники мощностей, решением которых можно определить соотношения сопротивлений, и мощности которые действуют в цепях переменного тока.
Векторная диаграмма напряжений представляет собой векторный треугольник напряжений
Последовательное соединение L R.
Любая катушка наматывается проволокой, а проволока обладает сопротивлением, которое приходится учитывать.
Получается, что реальная цепь, содержащая только L, просто невозможна. В некоторых случаях значением R пренебрегают, и получается, что вроде бы цепь с только L, на самом деле она конечно L R.
Реально, кроме проволоки, в цепи всегда есть и какие – то другие элементы R, поэтому интерес представляют именно цепи L R,
Ток, при последовательном соединении, один и тот же через все сопротивления, а напряжения разные, но общее напряжение не равно просто сумме напряжений на каждом сопротивлении, оно равно векторной сумме, то есть вектор общего напряжения равен сумме векторов напряжений на каждом участке. Для расчетов напряжений надо построить векторную диаграмму.
Векторная диаграмма строится так.
Получение переменного тока
Переменный ток может быть получен в простейшем генераторе с обмоткой из одного витка и с одним двухполюсным магнитом.
В реальных генераторах обмотка, конечно, имеет не один, а много витков. Магнитное поле создается, как правило, не магнитом, а электромагнитом. Число его полюсов может быть больше двух. Кроме того, в одних исполнениях генераторов магнит 1 неподвижен, а обмотка 2 вращается (рисунок 1, а), в других – обмотка 2 неподвижна, магнит 1 вращается (рисунок 1, б), что для конструирования и обслуживания весьма существенно, но принципиально совершенно безразлично. Почему? Потому, что для генерирования переменной электродвижущей силы (э. д
с.) важно лишь, чтобы витки обмотки пересекались магнитными силовыми линиями, а это в равной степени достигается как в том, так и в другом случае
Рисунок 1. Принцип получения переменного тока в генераторах
При вращении обмотки (магнита) она (он) последовательно во времени занимает различные положения относительно магнитного поля (обмотки). Сначала обмотка, плоскость которой перпендикулярна магнитному полю, находится на нейтрали, то есть между полюсами, как показано на рисунке 2, а. При этом проводники как бы скользят вдоль силовых линий и э. д. с. в них не возникает. Затем один проводник (его торец красный) приближается к северному полюсу N, а другой (зачерненный) к южному S (рисунок 2, б) и, наконец, они проходят под полюсами (рисунок 2, в). В этом положении проводники движутся перпендикулярно силовым линиям: э. д. с. достигает своего наибольшего значения. В проводниках, находящихся под разными полюсами, э. д. с. направлены различно: в одном из них – за плоскость чертежа, в другом – на нас. Но проводники, образующие виток, соединены друг с другом таким образом, что их э. д. с. складываются.
Рисунок 2. Изменение э. д. с. в течение одного периода
Далее проводники удаляются от полюсов (рисунок 2, г) и снова достигают нейтрали (рисунок 2, д): э. д. с. равна нулю.
Продолжая движение, проводник, который ранее проходил под северным полюсом, приближается к южному (рисунок 2, е); проводник, который был под южным полюсом, приближается к северному: направление э. д. с. меняется на обратное. Под полюсами (рисунок 2, ж) э. д. с. снова достигает наибольшего значения, но она отрицательна.
Наконец проводники удаляются от полюсов (рисунок 2, з) и опять выходят на нейтраль (рисунок 2, и): э. д. с. равна нулю. Далее при каждом обороте все периодически повторяется в той же последовательности.
Видео 1. Получение переменного электрического тока
Заключение
Итак, теперь стало понятно, как устроена «последняя миля» системы энергоснабжения и зачем нужен сдвиг по фазе ее питающих напряжений. На самом деле принцип разделения одного мощного процесса на несколько маломощных, но протекающих в разные моменты времени, не является чем-то уникальным. Например, этот же принцип используется в двигателях внутреннего сгорания, в которых цилиндры работают по очереди. По такому же принципу работают многофазные преобразователи постоянного напряжения на материнской плате компьютера, формирующие напряжения для питания процессора и других устройств. Однако использование такого подхода в системах электроснабжения является, на мой взгляд, одним из самых удачных.
Тем не менее, трехфазная система электроснабжения, несмотря на применение многих интересных технических решений, не лишена своих особенностей и недостатков. Например, наличие двух напряжений 230/400 В и возможность одно- и трехфазного подключения, с одной стороны, являются несомненными преимуществами, ведь это позволяет выбрать наиболее оптимальный способ соединения оборудования разной мощности. С другой стороны, при аварии, например, при обрыве нулевого провода, такая система способна вывести из строя все однофазное оборудование и даже стать причиной пожара. Но об этой особенности речь пойдет уже в следующей части цикла.